
Jednotkové kružnice trigonometrické funkce a aplikace
The jednotkový kruh je kruh o poloměru rovný 1, který je obvykle vystředěn v bodě (0,0) kartézského souřadného systému xy. Používá se ke snadnému definování trigonometrických poměrů úhlů pomocí pravoúhlých trojúhelníků.
Rovnice jednotkové kružnice se středem v počátku je:
Xdva + Ydva = 1
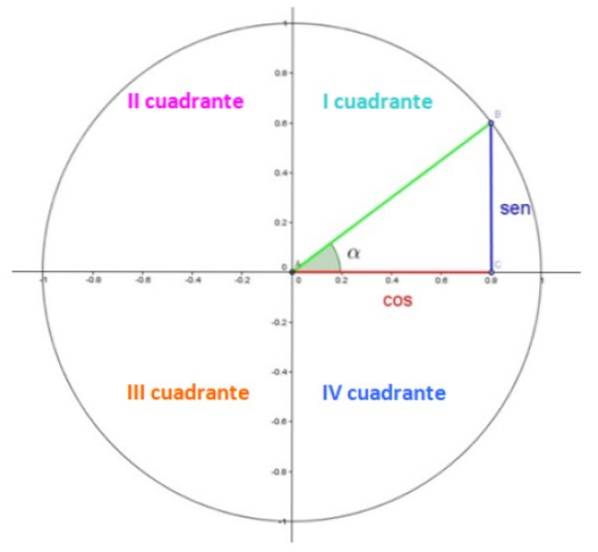
Na obrázku 1 máme jednotkovou kružnici, ve které je každá čtvrtina v kvadrantu. Kvadranty jsou očíslovány římskými číslicemi a počítají se proti směru hodinových ručiček.
V prvním kvadrantu je trojúhelník. Nohy, červené a modré, měří v tomto pořadí 0,8 a 0,6, zatímco přepona v zelené měří 1, protože se jedná o poloměr.
Ostrý úhel α je středový úhel ve standardní poloze, což znamená, že jeho vrchol se shoduje s bodem (0,0) a jeho počáteční strana s kladnou osou x. Úhel se měří proti směru hodinových ručiček a podle konvence se mu přiřazuje kladné znaménko.
V jednotkové kružnici jsou kosinové a sinusové souřadnice α souřadnice xay v bodě B, které jsou v uvedeném příkladu 0,8 a 0,6.
Z těchto dvou jsou definovány:
- tg α = sin α / cos α = 0,6 / 0,8 = 0,75
- sec α = 1 / cos α = 1 / 0,8 = 1,25
- cosec α = 1 / sin α = 1 / 0,6 = 1,66…
- ctg α = 1 / tg = 0,8 / 0,6 = 1,33…
Rejstřík článků
- 1 Aplikace kruhových jednotek
- 1.1 Referenční úhel
- 2 Vynesení grafů kosinu a sinu
- 2.1 Vlastnosti sinusových a kosinových funkcí
- 3 Vyřešená cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Aplikace kruhů jednotek
Pokud bychom se omezili na pravé trojúhelníky, trigonometrické poměry by platily pouze pro ostré úhly. S pomocí jednotkové kružnice je však výpočet trigonometrických poměrů rozšířen na libovolný úhel α.
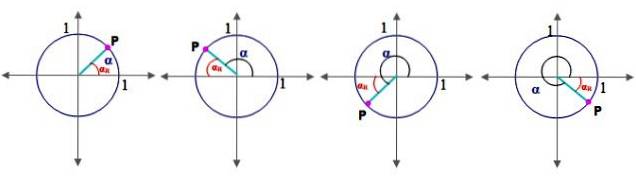
K tomu je nutné nejprve definovat koncept referenčního úhlu αR:
Referenční úhel
Nechť α je úhel ve standardní poloze (ten, jehož výchozí strana se shoduje s kladnou osou x), její referenční úhel αR je mezi jeho koncová strana a osa x. Obrázek 2 ukazuje referenční úhel pro úhly v kvadrantu I, II, III a IV.
Pro každý kvadrant se referenční úhel vypočítá takto:
-První kvadrant: αR = α
-Druhý kvadrant: αR = 180 ° - α
-Třetí kvadrant: αR = α - 180 °
-Čtvrtý kvadrant: αR = 360 ° - α
Všimněte si, že první kvadrant se úhel α shoduje s jeho referenčním úhlem. Trigonometrické poměry úhlu α jsou stejné jako jejich referenční úhel, se znaménky podle těch kvadrantů, ve kterých padá koncová strana α..
Jinými slovy, trigonometrické kosinové a sinusové poměry úhlu α se shodují se souřadnicemi bodu P, podle obrázku 2.
Na následujícím obrázku vidíme trigonometrické poměry některých pozoruhodných úhlů, jak je odvozeno z jednotkového kruhu.
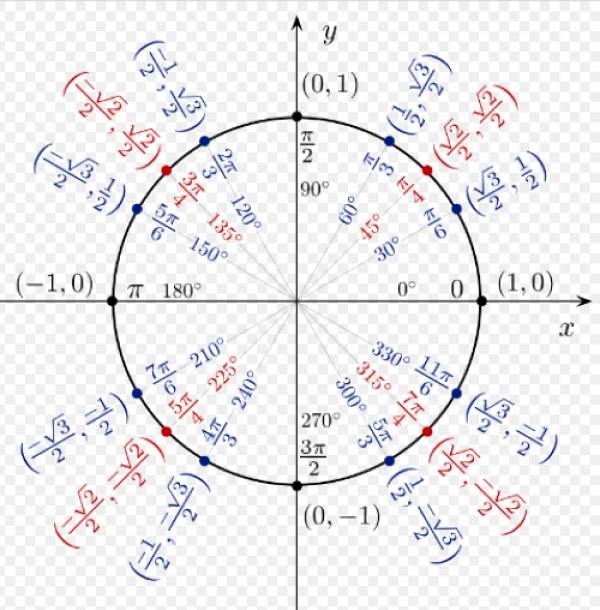
Kosinový a sinusový poměr jakéhokoli úhlu v I kvadrantu jsou všechny pozitivní. Pro α = 60 ° máme souřadnice (1/2; √3 / 2), které odpovídají cos 60 ° a sin 60 °.
Souřadnice α = 120 ° jsou (-1/2; √3 / 2), protože ve druhém kvadrantu je souřadnice x záporná.
Vynesení kosinusových a sinusových grafů
Pomocí jednotkové kružnice a souřadnic bodů P na ní je možné nakreslit grafy funkcí cos t a sin t, jak uvidíme níže.
K tomu se na jednotkové kružnici nacházejí různé polohy bodu P (t). Začneme grafem funkce f (t) = sin t.
Vidíme, že když přejdeme z t = 0 na t = π / 2 (90 °), hodnota sin t se zvyšuje, dokud nedosáhne 1, což je maximální hodnota.
Na druhou stranu od t = π / 2 do t = 3π / 2 hodnota sin t klesá od 1, prochází 0 při t = π, dokud nedosáhne svého minima -1 při t = 3π / 2.
Obrázek ukazuje graf prvního cyklu f (t) = sin t, který odpovídá prvnímu kruhu jednotkové kružnice, tato funkce je periodická s periodou 2π.
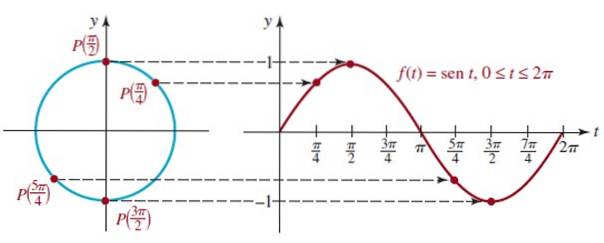
Analogickým postupem lze získat graf funkce f (t) = cos t, jak je znázorněno v následující animaci:
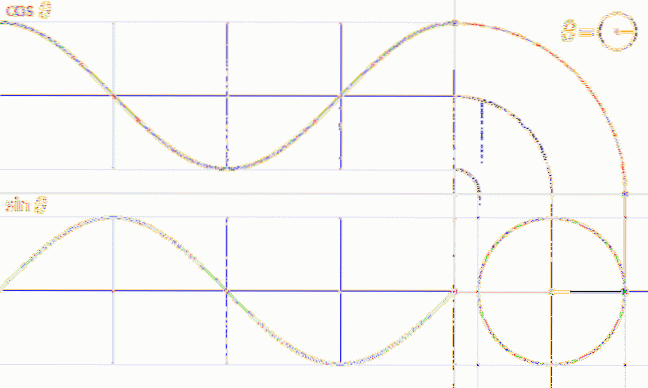
Vlastnosti sinusových a kosinových funkcí
-Obě funkce jsou spojité v množině reálných čísel a také periodické, s periodou 2π.
-Doménou funkcí f (t) = sin t a f (t) = cos t jsou všechna reálná čísla: (-∞, ∞).
-Pro rozsah nebo cestu sinu a kosinu máme interval [-1,1]. Závorky označují, že jsou zahrnuty -1 a 1.
- Nuly sin t jsou hodnoty, které odpovídají nπ s n celým číslem, zatímco nuly cos t jsou [(2n + 1) / 2] s n také celé číslo.
-Funkce f (t) = sin t je lichá, má symetrii o počátku, zatímco funkce cos t je sudá, její symetrie je kolem svislé osy.
Vyřešená cvičení
- Cvičení 1
Vzhledem k tomu, cos t = - 2/5, což je vodorovná souřadnice bodu P (t) na jednotkové kružnici ve druhém kvadrantu, získáte odpovídající svislou souřadnici sin t.
Řešení
Protože P (t) patří do jednotkového kruhu, ve kterém platí:
Xdva + Ydva = 1
Proto:
y = ± √ 1 - xdva
Protože P (t) je ve druhém kvadrantu, bude brána v úvahu kladná hodnota. Svislá souřadnice bodu P (t) je y:
y = √ 1 - (-2/5)dva = √ 0,84
- Cvičení 2
Matematický model teploty T ve stupních Fahrenheita v kterýkoli daný den, t hodin po půlnoci je dána:
T (t) = 50 + 10 sin [(π / 12) × (t - 8)]
S t mezi 0 a 24 hodinami. Nalézt:
a) Teplota v 8 hodin ráno.
b) Hodiny, během nichž T (t) = 60 ° F
c) Maximální a minimální teploty.
Řešení
V dané funkci dosadíme t = 8:
T (8) = 50 + 10 sin [(π / 12) × (t-8)] = 50 + 10 sin [(π / 12) × (8-8)] =
= 50 + 10 x hřích 0 = 50 ° F
Řešení b
50 + 10 sin [(π / 12) × (t-8)] = 60
Je to trigonometrická rovnice a my musíme vyřešit neznámé „t“:
10 sin [(π / 12) × (t-8)] = 60 - 50 = 10
sin [(π / 12) × (t-8)] = 1
Víme, že sin π / 2 = 1, proto musí být sinusový argument 1:
(π / 12) × (t-8) = π / 2
t-8 = 6
t = 14 h
Byl vyvozen závěr, že 14 hodin po půlnoci je teplota 60 °, tj. 14:00. Pokud k tomu dojde, po celý den (24 hodin) není čas.
Řešení c
Maximální teplota odpovídá hodnotě, při které sin [(π / 12) × (t-8)] = 1 a je 60 ° F. Na druhou stranu, minimum nastane, když sin [(π / 12) × (t-8)] = -1 a je 40ºF.
Reference
- Figuera, J. 1999. Mathematics. 1. místo Diverzifikovaný. Bolivarian Collegiate Edition.
- Hoffman, J. Výběr témat matematiky. Svazek 4.
- Jiménez, R. 2008. Algebra. Hala Prentice.
- Matematika je zábava. Obnoveno z: de: mathsisfun.com.
- Wikipedia. Identity a vzorce trigonometrie. Obnoveno z: es.wikipedia.org.
- Zill, D. 1984. Algebra a trigonometrie. Mcgraw kopec.



Zatím žádné komentáře