
Čtyřstranné prvky, vlastnosti, klasifikace, příklady
A čtyřúhelník je mnohoúhelník se čtyřmi stranami a čtyřmi vrcholy. Jejich protilehlé strany jsou ty, které nemají společné vrcholy, i když jsou po sobě jdoucích stran ty se společným vrcholem.
Ve čtyřúhelníku jsou sousední úhly ti, kteří sdílejí stranu, zatímco opačné úhly nemají společné žádné strany. Další důležitou charakteristikou čtyřúhelníku je součet jeho čtyř vnitřní úhly je dvojnásobek rovinného úhlu, tj. 360 ° nebo 2π radiány.
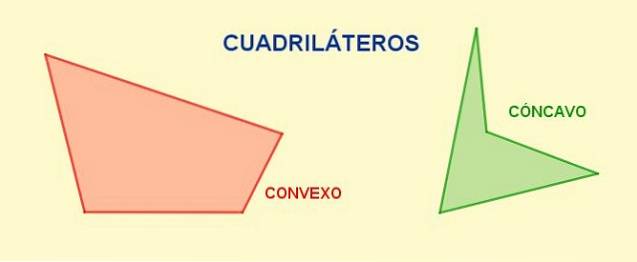
Úhlopříčky jsou segmenty, které spojují vrchol s jeho protikladem a v daném čtyřúhelníku lze z každého vrcholu nakreslit jednu úhlopříčku. Celkový počet úhlopříček v čtyřúhelníku jsou dvě.
Čtyřstěny jsou postavy známé lidstvu od starověku. Svědčí o tom archeologické záznamy i stavby, které dnes přežívají..
Podobně i dnes mají čtyřstěny stále důležitou přítomnost v každodenním životě každého člověka. Čtenář může tento formulář najít na obrazovce, na které se právě v tuto chvíli čte text, na oknech, dveřích, automobilových součástech a bezpočtu dalších míst..
Rejstřík článků
- 1 Klasifikace čtyřúhelníků
- 1.1 Druhy rovnoběžníku
- 2 lichoběžník
- 2.1 Druhy lichoběžníků
- 3 rovnoběžník
- 3.1 Plocha rovnoběžníku
- 3.2 Úhlopříčky rovnoběžníku
- 3.3 Zákon rovnoběžníků
- 4 Obdélník
- 4.1 Úhlopříčky obdélníku
- 5 náměstí
- 6 Kosočtverec
- 7 příkladů
- 7.1 Příklad 1
- 7.2 Příklad 2
- 7.3 Příklad 3
- 8 Cvičení vyřešena
- 8.1 - Cvičení 1
- 8.2 - Cvičení 2
- 9 Odkazy
Klasifikace čtyřúhelníků
Podle rovnoběžnosti protilehlých stran jsou čtyřúhelníky klasifikovány následovně:
- Lichoběžník, když neexistuje paralelismus a čtyřúhelník je konvexní.
- Trapéz, když existuje paralelismus mezi jedním párem protilehlých stran.
- Rovnoběžník, když jeho protilehlé strany jsou paralelní dva po druhém.
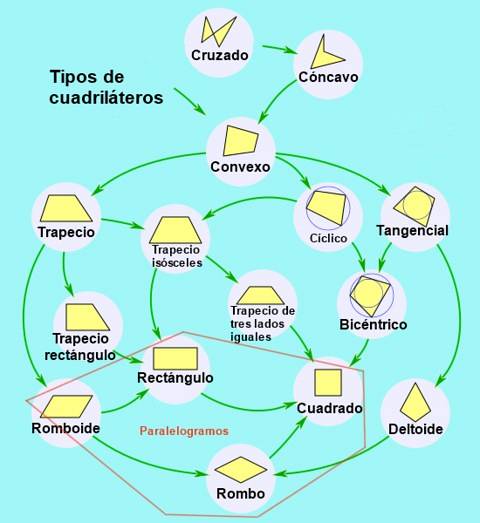
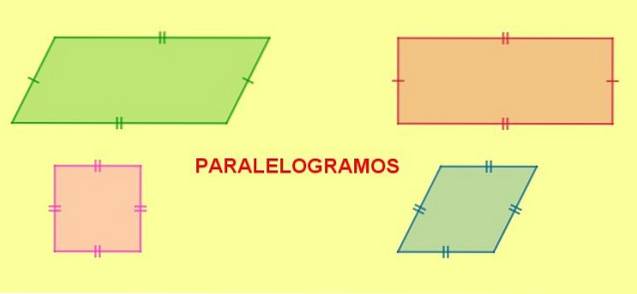
Druhy rovnoběžníku
Paralelogramy lze dále klasifikovat podle jejich úhlů a stran takto:
- Obdélník, je rovnoběžník, který má své čtyři vnitřní úhly stejné míry. Vnitřní úhly obdélníku tvoří pravý úhel (90 °).
- Náměstí, je obdélník se čtyřmi stranami stejné míry.
- diamant, je rovnoběžník se čtyřmi stejnými stranami, ale různými sousedními úhly.
- Kosodélník, rovnoběžník s různými sousedními úhly.
Trapéz
Lichoběžník je konvexní čtyřúhelník se dvěma rovnoběžnými stranami.
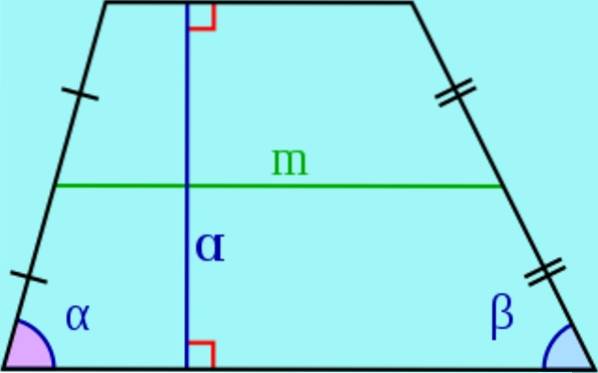
- V lichoběžníku se nazývají rovnoběžné strany základny a volají se neparalely postranní.
- The výška lichoběžníku je vzdálenost mezi dvěma základnami, tj. délka segmentu s konci u základen a kolmo k nim. Tento segment se také nazývá výška lichoběžníku..
- The medián je segment, který spojuje středy bočnic. Je možné ukázat, že medián je rovnoběžný se základnami lichoběžníku a jeho délka se rovná polosoučtu základen.
- Plocha lichoběžníku je jeho výška vynásobená poločtem základen:
Plocha lichoběžníku = výška * (základna 1 + základna 2) / 2
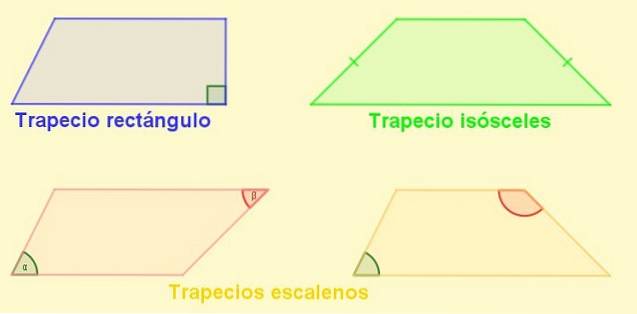
Druhy lichoběžníků
-Obdélník lichoběžník: Je ten, který má boční kolmici na základny. Tato boční je také výška lichoběžníku.
-Trapézové rovnoramenné: Ten se stranami stejné délky. V rovnoramenném lichoběžníku jsou úhly sousedící se základnami stejné.
-Scalene lichoběžník: Ten, jehož strany jsou různé délky. Jeho opačné úhly mohou být jeden ostrý a druhý tupý, ale může se také stát, že oba jsou tupé nebo oba jsou ostré..
Rovnoběžník
Rovnoběžník je čtyřúhelník, jehož protilehlé strany jsou rovnoběžné dvě po druhé. V rovnoběžníku jsou protilehlé úhly stejné a sousední úhly jsou doplňkové, nebo jinými slovy, sousední úhly přidávají až 180 °.
Pokud má rovnoběžník pravý úhel, budou všechny ostatní úhly také a výsledný údaj bude vyvolán obdélník. Ale pokud má obdélník také své sousední strany stejné délky, pak jsou všechny jeho strany stejné a výsledný údaj je a náměstí.
Pokud má rovnoběžník dvě sousední strany stejné délky, všechny jeho strany budou stejné délky a výsledný údaj je diamant.
Výška rovnoběžníku je segment s konci na jeho opačných stranách a kolmými na ně..
Plocha rovnoběžníku
Plocha rovnoběžníku je součinem základny a její výšky, přičemž základna je strana kolmá k výšce (obrázek 6).
Plocha rovnoběžníku = základna x výška = a. h
Úhlopříčky rovnoběžníku
Čtverec úhlopříčky, která začíná od vrcholu, se rovná součtu čtverců dvou stran sousedících s uvedeným vrcholem plus dvojnásobný součin těchto stran kosinusem úhlu tohoto vrcholu:
Fdva = adva + ddva + 2 a d Cos (α)
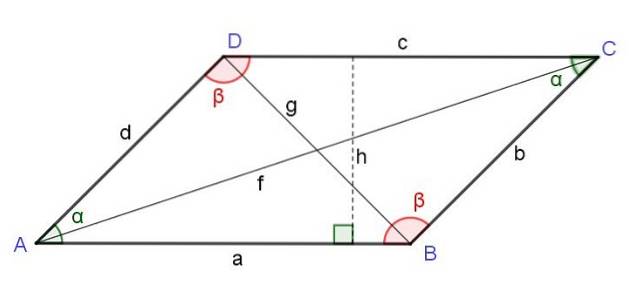
Čtverec úhlopříčky naproti vrcholu rovnoběžníku se rovná součtu čtverců dvou stran sousedících s uvedeným vrcholem a odečtením dvojitého produktu těchto stran kosinusem úhlu tohoto vrcholu:
Gdva = adva + ddva - 2 a d Cos (α)
Zákon rovnoběžníků
V libovolném rovnoběžníku se součet čtverců jeho stran rovná součtu čtverců úhlopříček:
nadva + bdva + Cdva + ddva = fdva + Gdva
Rectangle
Obdélník je čtyřúhelník, jehož protilehlé strany jsou paralelní dva po druhém a který má také pravý úhel. Jinými slovy, obdélník je typ rovnoběžníku s pravým úhlem. Za to, že jsou rovnoběžníky, obdélník má protilehlé strany stejné délky a = ca ab = d.
Ale jako v každém rovnoběžníku sousední úhly jsou doplňkové a opačné úhly stejné, v obdélníku, protože má pravý úhel, bude nutně tvořit pravé úhly v ostatních třech úhlech. A to v obdélníku všechny vnitřní úhly měří 90 ° nebo π / 2 radiány.
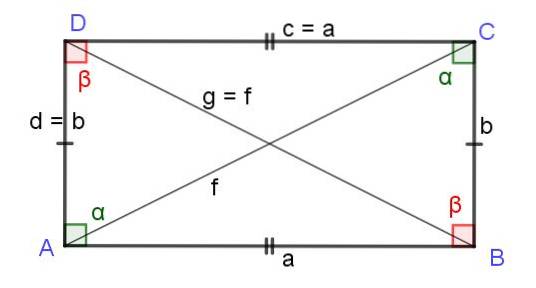
Úhlopříčky obdélníku
V obdélníku jsou úhlopříčky stejně dlouhé, jak bude ukázáno níže. Odůvodnění je následující; Obdélník je rovnoběžník se všemi svými pravými úhly, a proto zdědí všechny vlastnosti rovnoběžníku, včetně vzorce, který udává délku úhlopříček:
Fdva = adva+ ddva + 2 a d Cos (α)
Gdva = adva + ddva - 2 a d Cos (α)
s α = 90 °
Co Cos (90 °) = 0, pak se stane, že:
Fdva = gdva = adva + ddva
To je f = g, a tedy délky F Y G ze dvou úhlopříček obdélníku jsou stejné a jejich délka je dána vztahem:
Délka úhlopříček obdélníku = √ (adva + bdva)
Také, pokud je v obdélníku se sousedními stranami na Y b jedna strana je brána jako základna, druhá strana bude výška a následně bude plocha obdélníku:
Plocha obdélníku = a x b.
Obvod je součtem všech stran obdélníku, ale protože protiklady jsou stejné, vyplývá z toho, že pro obdélník se stranami na Y b obvod je dán následujícím vzorcem:
Obvod obdélníku = 2 (a + b)
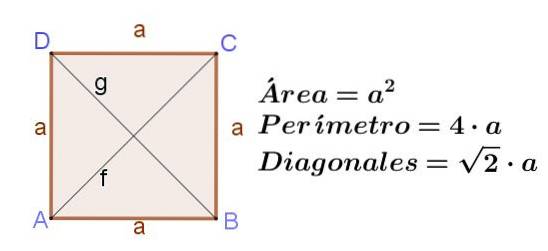
Náměstí
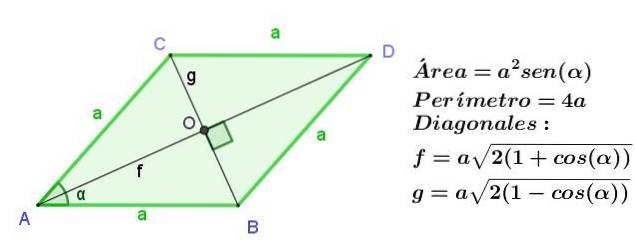
Čtverec je obdélník se sousedními stranami stejné délky. Pokud má čtverec stranu na, pak jeho úhlopříčky F Y G mají stejnou délku, která je f = g = (√2) a.
Plocha čtverce je jeho strana na druhou:
Plocha čtverce = adva
Obvod čtverce je dvojnásobek strany:
Obvod čtverce = 4 a
diamant
Kosočtverec je rovnoběžník se sousedními stranami stejné délky, ale stejně jako v rovnoběžníku jsou protilehlé strany stejné, všechny strany kosočtverce mají stejnou délku.
Úhlopříčky kosočtverce mají různou délku, ale protínají se v pravých úhlech.
Příklady
Příklad 1
Ukažte, že v čtyřúhelníku (nepřekříženém) se vnitřní úhly sčítají do 360 °.
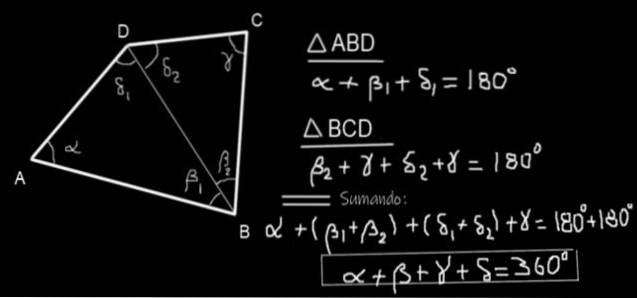
Uvažuje se o čtyřúhelníku ABCD (viz obrázek 10) a nakreslí se diagonální BD. Jsou vytvořeny dva trojúhelníky ABD a BCD. Součet vnitřních úhlů trojúhelníku ABD je:
α + β1 + δ1 = 180 °
A součet vnitřních úhlů trojúhelníku BCD je:
β2 + γ + δdva = 180 °
Přidáním dvou rovnic získáme:
α + β1 + δ1 + βdva + γ + δdva = 180 ° + 180 °
Seskupení:
α + (β1 + βdva) + (51 + δdva) + γ = 2 * 180 °
Seskupením a přejmenováním se nakonec ukazuje, že:
α + β + δ + γ = 360 °
Příklad 2
Ukažte, že medián lichoběžníku je rovnoběžný s jeho základnami a jeho délka je poločetem základen.
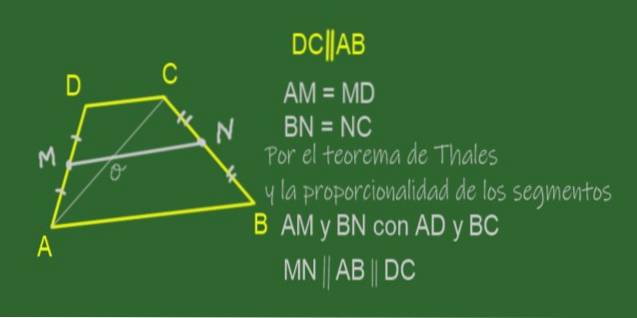
Medián lichoběžníku je segment, který spojuje středy jeho stran, tj. Nerovnoběžné strany. V lichoběžníku ABCD zobrazeném na obrázku 11 je medián MN.
Protože M je střed AD a N je střed BC, je pravda, že poměry AM / AD a BN / BC jsou stejné.
To znamená, že AM je úměrný BN ve stejném poměru jako AD k BC, takže jsou dány podmínky pro použití Thalesovy (vzájemné) věty, která uvádí následující:
"Pokud jsou proporcionální segmenty určeny ve třech nebo více liniích oříznutých dvěma secanty, pak jsou všechny tyto linie paralelní".
V našem případě dochází k závěru, že přímky MN, AB a DC jsou navzájem rovnoběžné, proto:
„L.medián lichoběžníku je rovnoběžný s jeho základnami".
Nyní bude použita Thalesova věta:
"Sada rovnoběžek řezaných dvěma nebo více sekanty určuje proporcionální segmenty".
V našem případě AD = 2 AM, AC = 2 AO, takže trojúhelník DAC je podobný trojúhelníku MAO a následně DC = 2 MO.
Podobný argument nám umožňuje potvrdit, že CAB je podobný CON, kde CA = 2 CO a CB = 2 CN. Z toho okamžitě vyplývá, že AB = 2 ZAPNUTO.
Stručně řečeno, AB = 2 ON a DC = 2 MO. Takže při přidávání máme:
AB + DC = 2 ON + 2 MO = 2 (MO + ON) = 2 MN
Nakonec je MN vymazáno:
MN = (AB + DC) / 2
A dochází k závěru, že medián lichoběžníku měří poloviční součet bází, nebo jinými slovy: medián měří součet bází vydělený dvěma.
Příklad 3
Ukažte, že v kosočtverci se úhlopříčky protínají v pravých úhlech.

Tabule na obrázku 12 ukazuje potřebnou konstrukci. Nejprve se nakreslí rovnoběžník ABCD s AB = BC, tj. Kosočtverec. Diagonály AC a DB určují osm úhlů zobrazených na obrázku.
Pomocí věty (a.i.p.), která uvádí, že alternativní vnitřní úhly mezi rovnoběžkami řezanými sekánem určují stejné úhly, můžeme stanovit následující:
α1 = γ1, a2 = γ2, δ1 = Β1 a δ2 = β2. (*)
Na druhou stranu, protože sousední strany kosočtverce mají stejnou délku, jsou určeny čtyři rovnoramenné trojúhelníky:
DAB, BCD, CDA a ABC
Nyní je vyvolána věta o trojúhelníku (rovnoramenném), která říká, že úhly sousedící se základnou mají stejnou míru, z čehož se vyvozuje, že:
δ1 = β2, δ2 = β1, α2 = γ1 a α1 = γ2 (**)
Pokud jsou vztahy (*) a (**) kombinovány, je dosaženo následující rovnosti úhlu:
α1 = α2 = γ1 = γ1 na jedné straně a β1 = Β2 = δ1 = δ2 na straně druhé.
Připomeňme teorém o rovných trojúhelnících, který říká, že dva trojúhelníky se stejnou stranou mezi dvěma stejnými úhly jsou stejné, máme:
AOD = AOB a následně také úhly ∡AOD = ∡AOB.
Potom ∡AOD + ∡AOB = 180 °, ale protože oba úhly mají stejnou míru, máme 2 ∡AOD = 180 °, což znamená, že ∡AOD = 90 °.
To znamená, že je geometricky ukázáno, že úhlopříčky kosočtverce se protínají v pravých úhlech.
Cvičení vyřešena
- Cvičení 1
Ukažte, že v pravém lichoběžníku jsou nepravé úhly doplňkové.
Řešení
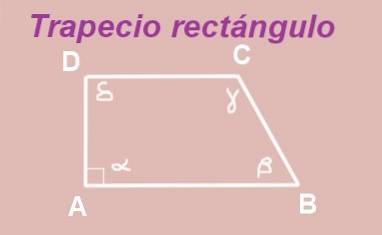
Lichoběžník ABCD je konstruován s bázemi AB a DC paralelně. Vnitřní úhel vrcholu A je pravý (měří 90 °), takže máme pravý lichoběžník.
Úhly α a δ jsou vnitřní úhly mezi dvěma rovnoběžkami AB a DC, proto jsou stejné, tj. Δ = α = 90 °.
Na druhou stranu se ukázalo, že součet vnitřních úhlů čtyřúhelníku se sčítá až 360 °, což je:
α + β + γ + δ = 90º + β + 90º + δ = 360º.
Výše uvedené vede k:
β + δ = 180 °
Potvrzení toho, co se chtělo ukázat, že úhly β a δ jsou doplňkové.
- Cvičení 2
Rovnoběžník ABCD má AB = 2 cm a AD = 1 cm, navíc úhel BAD je 30 °. Určete plochu uvedeného rovnoběžníku a délku jeho dvou úhlopříček.
Řešení
Plocha rovnoběžníku je součinem délky jeho základny a jeho výšky. V tomto případě bude jako základ brána délka segmentu b = AB = 2 cm, druhá strana má délku a = AD = 1 cm a výška h bude vypočítána takto:
h = AD * Sen (30 °) = 1 cm * (1/2) = ½ cm.
Takže: Plocha = b * h = 2 cm * ½ cm = 1 cmdva.
Reference
- C. E. A. (2003). Prvky geometrie: s cvičeními a geometrií kompasu. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematika 2. Grupo Redakční Patria.
- Freed, K. (2007). Objevte mnohoúhelníky. Benchmark Education Company.
- Hendrik, V. (2013). Zobecněné polygony. Birkhäuser.
- IGER. (s.f.). Matematika v prvním semestru Tacaná. IGER.
- Jr. geometrie. (2014). Mnohoúhelníky. Lulu Press, Inc..
- Miller, Heeren a Hornsby. (2006). Mathematics: Reasoning And Applications (desáté vydání). Pearson Education.
- Patiño, M. (2006). Matematika 5. Redakční program.
- Wikipedia. Čtyřúhelníky. Obnoveno z: es.wikipedia.com


Zatím žádné komentáře