The aditivní rozklad kladného celého čísla je vyjádřit jej jako součet dvou nebo více kladných celých čísel. Máme tedy, že číslo 5 lze vyjádřit jako 5 = 1 + 4, 5 = 2 + 3 nebo 5 = 1 + 2 + 2. Každý z těchto způsobů zápisu čísla 5 nazýváme aditivní rozklad.
Pokud věnujeme pozornost, vidíme, že výrazy 5 = 2 + 3 a 5 = 3 + 2 představují stejnou kompozici; oba mají stejná čísla. Kvůli pohodlí je však každý z přídavků obvykle psán podle kritéria od nejnižší po nejvyšší.
Rejstřík článků
Jako další příklad si můžeme vzít číslo 27, které můžeme vyjádřit jako:
27 = 7 + 10 + 10
27 = 9 + 9 + 9
27 = 3 + 6 + 9 + 9
27 = 9 + 18
Aditivní rozklad je velmi užitečný nástroj, který nám umožňuje posílit naše znalosti o číslovacích systémech.
Když máme čísla s více než dvěma číslicemi, můžeme je konkrétně rozložit v násobcích 10, 100, 1000, 10 000 atd., Které je tvoří. Tento způsob psaní libovolného čísla se nazývá kanonický aditivní rozklad. Například číslo 1456 lze rozložit následovně:
1456 = 1000 + 400+ 50 + 6
Pokud máme číslo 20 846 295, jeho kanonický aditivní rozklad bude:
20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.
Díky tomuto rozkladu vidíme, že hodnota dané číslice je dána pozicí, kterou zaujímá. Vezměme si jako příklad čísla 24 a 42:
24 = 20 + 4
42 = 40 +2
Zde vidíme, že v 24 má 2 hodnotu 20 jednotek a 4 hodnotu 4 jednotek; na druhou stranu, v 42 má 4 hodnotu 40 jednotek a 2 ze dvou jednotek. Ačkoli tedy obě čísla používají stejné číslice, jejich hodnoty jsou zcela odlišné kvůli poloze, kterou zaujímají.
Jednou z aplikací, které můžeme dát aditivnímu rozkladu, jsou určité typy důkazů, ve kterých je velmi užitečné vidět kladné celé číslo jako součet ostatních.
Vezměme si jako příklad následující větu s příslušnými důkazy.
- Nechť Z je čtyřmístné celé číslo, pak Z je dělitelné 5, pokud je jeho počet jednotek nula nebo pět.
Vzpomeňme si, co je to dělitelnost. Pokud máme celá čísla „a“ a „b“, říkáme, že „a“ rozděluje „b“, pokud existuje celé číslo „c“ takové, že b = a * c.
Jedna z vlastností dělitelnosti nám říká, že pokud jsou „a“ a „b“ dělitelné písmenem „c“, pak je dělitelný také „a-b“..
Nechť Z je čtyřciferné celé číslo; proto můžeme psát Z jako Z = ABCD.
Pomocí kanonického aditivního rozkladu máme:
Z = A * 1000 + B * 100 + C * 10 + D
Je jasné, že A * 1000 + B * 100 + C * 10 je dělitelné 5. Z tohoto důvodu máme, že Z je dělitelné 5, pokud Z - (A * 1000 + B * 100 + C * 10) je dělitelné 5.
Ale Z - (A * 1000 + B * 100 + C * 10) = D a D je jednociferné číslo, takže jediný způsob, jak to lze dělit 5, je, aby to bylo 0 nebo 5.
Proto je Z dělitelné 5, pokud D = 0 nebo D = 5.
Všimněte si, že pokud má Z n číslic, důkaz je přesně stejný, změní se pouze to, že nyní napíšeme Z = A1NAdva… TOn a cílem by bylo dokázat, že An je nula nebo pět.
Říkáme, že oddíl kladného celého čísla je způsob, jakým můžeme napsat číslo jako součet kladných celých čísel.
Rozdíl mezi aditivním rozkladem a oddílem spočívá v tom, že zatímco první z nich usiluje o to, aby jej bylo možné alespoň rozložit na dvě nebo více příloh, oddíl toto omezení nemá.
Máme tedy následující:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 2 + 2
Výše uvedené jsou oddíly 5.
To znamená, že máme, že každý rozklad aditiv je oddílem, ale ne každý oddíl je nutně rozkladem aditiv..
V teorii čísel základní věta aritmetiky zaručuje, že každé celé číslo lze jednoznačně napsat jako produkt prvočísel.
Při studiu oddílů je cílem zjistit, kolik způsobů lze napsat celé kladné číslo jako součet ostatních celých čísel. Proto definujeme funkci oddílu, jak je uvedeno níže.
Funkce oddílu p (n) je definována jako počet způsobů, jak lze celé kladné číslo n zapsat jako součet kladných celých čísel.
Vrátíme-li se k příkladu 5, máme to:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 1 + 1 + 1
Tedy p (5) = 7.
Oba oddíly i aditivní rozklad čísla n lze znázornit geometricky. Předpokládejme, že máme aditivní rozklad n. V tomto rozkladu lze dodatky uspořádat tak, aby členové součtu byly seřazeny od nejmenšího k největšímu. Takže, dobře:
n = a1 + nadva + na3 +… + Ar s
na1 ≤ adva ≤ a3 ≤… ≤ ar.
Tento rozklad můžeme graficky znázornit následujícím způsobem: v první řadě označíme a1-body, pak v dalším označímedva-body atd., dokud nedosáhnete ar.
Vezměme si například číslo 23 a jeho následující rozklad:
23 = 5 + 4 + 7 + 3 + 1 +3
Objednáme si tento rozklad a máme:
23 = 1 + 3 + 3 + 4+ 5 + 7
Odpovídající graf by byl:
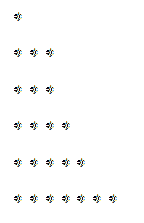
Podobně, pokud čteme uvedený graf svisle místo vodorovně, můžeme získat rozklad, který je možná odlišný od předchozího. V příkladu 23 vyniká:
Takže máme 23, můžeme to také napsat jako:
23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.
Zatím žádné komentáře