Dynamika systému příkladů částic, cvičení

The dynamika částicového systému Skládá se z aplikace Newtonových pohybových zákonů na sadu částic, které mohou být diskrétní (částice lze spočítat) nebo být součástí rozšířeného objektu, v tomto případě je systém spojitý.

Abychom vysvětlili pohyb soustavy částic, je nepohodlné analyzovat každou z nich zvlášť a zjistit, jaké síly na ni působí. Místo toho je definován reprezentativní bod množiny, který se nazývá Mass centrum.

Popis pohybu těžiště nabízí velmi přesný přehled o celkovém pohybu celku a umožňuje také aplikovat Newtonovy zákony způsobem analogickým tomu, kdy je objekt považován za bezrozměrnou částici.

Tento nejnovější model, tzv částicový model, Je to dobré pro popis překladů a také tehdy, když nepotřebujete brát v úvahu rozměry objektu. Ale běžné objekty mají velikost a pokud mají také rotační pohyb, je třeba vzít v úvahu body, na které působí síly.

Rejstřík článků

• 1 Příklady
  • 1.1 Země a Měsíc
  • 1.2 Rozšířené objekty
• 2 Těžiště soustavy částic
  • 2.1 CM pohyb
  • 2.2 Síla na CM
• 3 Cvičení vyřešeno
  • 3.1 Řešení a
  • 3.2 Řešení b
  • 3.3 Řešení c
• 4 Odkazy

Příklady

Země a Měsíc

Sada diskrétních částic m₁, m_dva, m₃... který se nakonec pohybuje s ohledem na počátek souřadného systému, kvůli nějaké výsledné síle působící na ně, je dobrým příkladem částicového systému.

Země může být považována za jednu částici a Měsíc za druhou, pak obě tvoří soustavu 2 částic působením gravitační síly Slunce..

Rozšířené objekty

Osoba, zvíře nebo jakýkoli předmět v životním prostředí může být také považován za soustavu částic, pouze pokud jsou tak malé, že je nelze spočítat jeden po druhém. Jedná se o spojitý systém, ale s přihlédnutím k určitým úvahám je jeho léčba stejná jako u diskrétního systému.

Níže jsou uvedeny podrobnosti.

Těžiště soustavy částic

Pro zahájení studia částicového systému musíme najít těžiště (CM), což je bod, kde je soustředěna veškerá hmota systému..

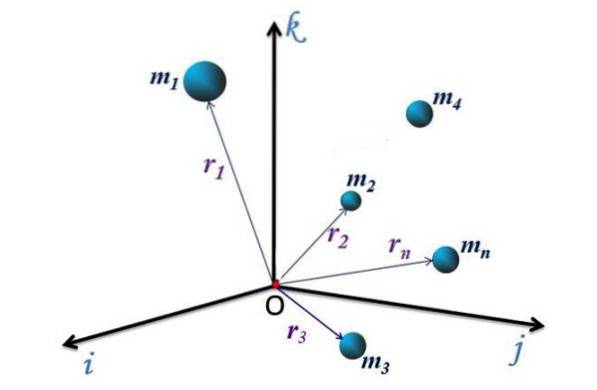
Pro diskrétní systém na obrázku 1 s n částice, každá má polohový vektor směrovaný od počátku O souřadnicového systému do bodu P (x, y, z), kde je částice. Tyto vektory jsou označeny jako r₁, r_dva, r₃... r_n.

Souřadnice CM se vypočítají pomocí následujících rovnic:

Kde je každá z hmot množiny vyjádřena jako m₁, m_dva, m₃... m_n. Všimněte si, že součet ∑ m_i se rovná celkové hmotnosti M sestavy. Pokud je systém spojitý, jsou součty nahrazeny integrály.

Každý z kolmých směrů je reprezentován jednotkovými vektory i, j Y k, proto je označen polohový vektor CM r_CM, lze vyjádřit:

r_CM = x_CM i + Y_CM j + z_CM k

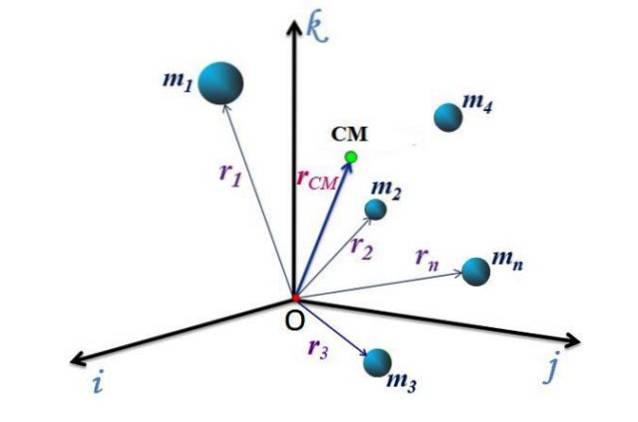
CM pohyb

Jakmile je známo umístění těžiště, platí známé pohybové rovnice. Rychlost CM je první derivací polohy s ohledem na čas:

V tomto případě má systém celkovou hybnost P který se vypočítá jako součin celkové hmotnosti systému a rychlosti těžiště:

P = M ∙proti_CM

Alternativně lze celkovou hybnost systému vypočítat přímo:

P = m₁proti₁ + m_dvaproti_dva + m₃proti₃ +…. = ∑ m_i proti_i

Zatímco zrychlení CM je derivací rychlosti:

Síla na CM

Síly působící na soustavu částic mohou být:

• Vnitřní síly v důsledku interakcí mezi stejnými částicemi.
• Vnější síly způsobené agenty mimo systém.

Protože vnitřní síly jsou prezentovány v párech, stejné velikosti a směru, ale podle třetího Newtonova zákona platí opačné směry, je pravda, že:

∑ F_int = 0

Proto vnitřní síly nemění pohyb celku, ale jsou velmi důležité pro určení vnitřní energie..

Pokud je systém izolovaný a neexistují žádné vnější síly, podle Newtonova prvního zákona je těžiště v klidu nebo se pohybuje rovnoměrným přímočarým pohybem. Jinak těžiště zažívá zrychlení dané:

∑ F_ext = M ∙na_CM

Kde M je celková hmotnost systému. Výše uvedená rovnice může být napsána takto:

A to znamená, že vnější síla je ekvivalentní časové změně hybnosti, dalšímu způsobu vyjádření druhého Newtonova zákona a stejnému, který použil slavný anglický fyzik ve své knize Zásada.

Cvičení vyřešeno

Těžiště 2-částicového systému je v určitém okamžiku na ose x, v poloze x = 2,0 ma pohybuje se rychlostí 5,0 m / s ve stejném směru a v kladném směru. Pokud je jedna z částic v počátku a druhá o hmotnosti 0,1 kg je v klidu v x = 8,0 m, vypočítejte:

a) Hmotnost částice, která je v počátku.

b) Množství pohybu systému

c) Jaká je rychlost částice v počátku?

Řešení

Z rovnice pro polohu těžiště:

r_CM = x_CM i + Y_CM j + z_CM k = 2,0 m i

Protože CM má pouze souřadnici x, použije se pouze první rovnice trojice, která byla uvedena dříve:

Nyní jsou souřadnice nahrazeny, pokud je částice v počátku označena jako číslo 1 a druhá jako číslo 2, numerická data jsou:

X₁ = 0 m, x_dva = 8,0 m, m_dva = 0,1 kg, x_CM = 2,0 m

Zbývající:

Řešení b

Velikost pohybu systému se vypočítá podle:

P = M ∙proti_CM

Celková hmotnost M se rovná:

M = 0,3 kg + 0,1 kg = 0,4 kg

Proto:

P = 0,4 kg ∙ 5,0 m / s i = 2 kg.m / s i

Řešení c

Z rovnice pro P dvoučásticového systému, to se vyčistí proti₁, protože jsou známa další data, protože tvrzení říká, že částice 2 je v klidu, proto:

proti_dva = 0 

Y P jednoduše to vypadá jako:

P = m₁proti₁

proti₁ = P / m₁ = 2 kg.m / s i / 0,3 kg = 6,67 m / s i

Reference

1. Duke University. Systémy částic. Obnoveno z: webhome.phy.duke.edu.
2. Rex, A. 2011. Základy fyziky. Pearson.
3. Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vyd. 1. díl Pearson.
4. Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7. Ed. Cengage Learning.
5. Tipler, P. (2006) Fyzika pro vědu a technologii. 5. vyd. Svazek 1. Redakční reverté.