The Poissonovo rozdělení je diskrétní rozdělení pravděpodobnosti, jehož prostřednictvím je možné zjistit pravděpodobnost, že při velké velikosti vzorku a během určitého intervalu dojde k události, jejíž pravděpodobnost je malá.
Často lze místo binomického rozdělení použít Poissonovo rozdělení, pokud jsou splněny následující podmínky: velký vzorek a malá pravděpodobnost.
Siméon-Denis Poisson (1781-1840) vytvořil tuto distribuci, která nese jeho jméno, což je velmi užitečné, pokud jde o nepředvídatelné události. Poisson publikoval své výsledky v roce 1837, výzkumnou práci o pravděpodobnosti výskytu chybných trestních rozsudků.
Později další vědci přizpůsobili distribuci v jiných oblastech, například počet hvězd, které lze najít v určitém objemu prostoru, nebo pravděpodobnost, že voják zemřel kopem koně.
Rejstřík článků
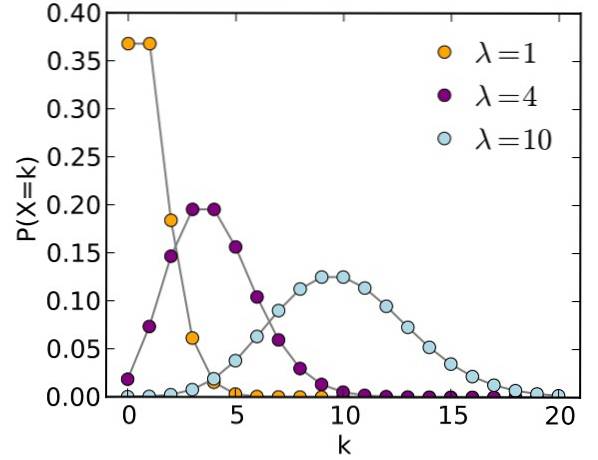
Matematická forma Poissonova rozdělení je následující:
- μ (někdy se také označuje jako λ) je průměr nebo parametr distribuce
- Eulerovo číslo: e = 2,71828
- Pravděpodobnost získání y = k je P
- k je počet úspěchů 0, 1,2,3 ...
- n je počet testů nebo událostí (velikost vzorku)
Diskrétní náhodné proměnné, jak naznačuje jejich název, závisí na náhodě a berou pouze diskrétní hodnoty: 0, 1, 2, 3, 4 ..., k.
Průměr distribuce je dán vztahem:
Odchylka σ, která měří šíření dat, je dalším důležitým parametrem. Pro Poissonovo rozdělení je to:
σ = μ
Poisson určil, že když n → ∞ a p → 0, průměrná μ - také volala očekávaná hodnota- má sklon ke konstantě:
μ → konstantní
Důležité: p je pravděpodobnost výskytu události s přihlédnutím k celkové populaci, zatímco P (y) je Poissonova předpověď na vzorku.
Poissonovo rozdělení má následující vlastnosti:
-Velikost vzorku je velká: n → ∞.
-Uvažované události nebo události jsou navzájem nezávislé a vyskytují se náhodně.
-Pravděpodobnost P tu určitou událost Y dochází během určitého časového období je velmi malý: P → 0.
-Pravděpodobnost, že v časovém intervalu dojde k více než jedné události, je 0.
-Průměrná hodnota se blíží konstantě dané: μ = n.p (n je velikost vzorku)
-Protože disperze σ se rovná μ, protože přijímá větší hodnoty, stává se variabilita také větší.
-Události musí být rovnoměrně rozloženy v použitém časovém intervalu.
-Sada možných hodnot událostí Y je: 0,1,2,3,4 ... .
-Součet i proměnné, které sledují Poissonovo rozdělení, je také další Poissonovou proměnnou. Jeho průměrná hodnota je součtem průměrných hodnot těchto proměnných.
Poissonovo rozdělení se liší od binomického rozdělení následujícími důležitými způsoby:
-Binomické rozdělení je ovlivněno velikostí vzorku n i pravděpodobností P, ale Poissonovo rozdělení je ovlivněno pouze průměrem μ.
-V binomickém rozdělení jsou možné hodnoty náhodné proměnné Y jsou 0,1,2,…, N, na druhou stranu v Poissonově rozdělení neexistuje horní limit pro tyto hodnoty.
Poisson zpočátku aplikoval svou slavnou distribuci na právní případy, ale na průmyslové úrovni bylo jedním z jeho prvních použití výroba piva. V tomto procesu se pro fermentaci používají kvasinkové kultury.
Kvasinky se skládají ze živých buněk, jejichž populace je v průběhu času proměnlivá. Při výrobě piva je nutné přidat potřebné množství, proto je nutné znát množství buněk, které jsou na jednotku objemu.
Během druhé světové války byla Poissonova distribuce použita ke zjištění, zda Němci skutečně mířili na Londýn z Calais, nebo jen náhodně stříleli. To bylo důležité pro spojence, aby zjistili, jak dobrá byla tato technologie nacistům k dispozici..
Aplikace Poissonovy distribuce vždy odkazují na počty v čase nebo počty v prostoru. A protože pravděpodobnost výskytu je malá, je také známá jako „zákon vzácných událostí“.
Zde je seznam událostí, které spadají do jedné z těchto kategorií:
-Záznam částic v radioaktivním rozpadu, který má rád růst kvasinkových buněk, je exponenciální funkcí.
-Počet návštěv určité webové stránky.
-Příchod lidí ve frontě na zaplacení nebo účast (teorie front).
-Počet aut, která projdou určitým bodem na silnici během daného časového intervalu.
-Mutace v určitém řetězci DNA po vystavení záření.
-Počet meteoritů o průměru větším než 1 m klesl za rok.
-Vady na metr čtvereční látky.
-Počet krvinek v 1 kubickém centimetru.
-Hovory za minutu na telefonní ústřednu.
-Čokoládové lupínky přítomné v 1 kg těsta na dorty.
-Počet stromů napadených určitým parazitem na 1 hektaru lesa.
Všimněte si, že tyto náhodné proměnné představují počet výskytů události během pevně stanoveného časového období (volání za minutu na telefonní ústřednu) nebo daná oblast vesmíru (vady látky na metr čtvereční).
Tyto události, jak již bylo stanoveno, jsou nezávislé na čase, který uplynul od posledního výskytu..
Poissonovo rozdělení je dobrou aproximací k binomickému rozdělení, pokud:
-Velikost vzorku je velká: n ≥ 100
-Pravděpodobnost p je málo: p ≤ 0,1
- μ je v pořadí: np ≤ 10
V takových případech je Poissonovo rozdělení vynikajícím nástrojem, protože v těchto případech může být obtížné použít binomické rozdělení..
Seismologická studie určila, že za posledních 100 let došlo po celém světě k 93 velkým zemětřesením, minimálně 6,0 Richterovy stupnice - logaritmické -. Předpokládejme, že Poissonovo rozdělení je v tomto případě vhodným modelem. Nalézt:
a) Průměrný výskyt velkých zemětřesení za rok.
b) Ano P (y) je pravděpodobnost výskytu Y zemětřesení během náhodně vybraného roku, vyhledejte následující pravděpodobnosti:
P(0), P(1), P (dva), P (3), P (4), P (5), P (6) a P (7).
c) Skutečné výsledky studie jsou následující:
- 47 let (0 zemětřesení)
- 31 let (1 zemětřesení)
- 13 let (2 zemětřesení)
- 5 let (3 zemětřesení)
- 2 roky (4 zemětřesení)
- 0 let (5 zemětřesení)
- 1 rok (6 zemětřesení)
- 1 rok (7 zemětřesení)
Jak se tyto výsledky srovnávají s výsledky získanými v části b? Je Poissonovo rozdělení dobrou volbou pro modelování těchto událostí?
a) Zemětřesení jsou události, jejichž pravděpodobnost p je malý a uvažujeme o omezeném časovém období jednoho roku. Průměrný počet zemětřesení je:
μ = 93/100 zemětřesení / rok = 0,93 zemětřesení za rok.
b) Pro výpočet požadovaných pravděpodobností jsou hodnoty nahrazeny vzorcem uvedeným na začátku:
y = 2
μ = 0,93
e = 2,71828
Je to docela méně než P (2).
Výsledky jsou uvedeny níže:
P (0) = 0,395, P (1) = 0,367, P (2) = 0,171, P (3) = 0,0529, P (4) = 0,0123, P (5) = 0,00229, P (6) = 0,000355, P (7) = 0,0000471.
Mohli bychom například říci, že existuje 39,5% pravděpodobnost, že v daném roce nenastane žádné velké zemětřesení. Nebo že v daném roce došlo k 5,29% ze 3 velkých zemětřesení.
c) Frekvence jsou analyzovány vynásobením n = 100 let:
39,5; 36,7; 17,1; 5,29; 1,23; 0,229; 0,0355 a 0,00471.
Například:
- Frekvence 39,5 naznačuje, že za 39,5 ze 100 let dojde k 0 velkým zemětřesením, dalo by se říci, že je to docela blízko skutečnému výsledku 47 let bez jakéhokoli většího zemětřesení..
Porovnejme další Poissonův výsledek se skutečnými výsledky:
- Získaná hodnota 36,7 znamená, že v 37letém období dojde k 1 velkému zemětřesení. Skutečným výsledkem je, že za 31 let došlo k 1 velkému zemětřesení, což je dobrá shoda s modelem.
- Očekává se 17,1 roku se 2 velkými zemětřeseními a je známo, že za 13 let, což je blízká hodnota, došlo skutečně ke 2 velkým zemětřesením.
Poissonův model je proto pro tento případ přijatelný.
Jedna společnost odhaduje, že počet komponent, které selžou před dosažením 100 provozních hodin, následuje Poissonovo rozdělení. Pokud je v té době průměrný počet poruch 8, najděte následující pravděpodobnosti:
a) Že součást selže za 25 hodin.
b) Selhání méně než dvou komponent za 50 hodin.
c) Selhání nejméně tří komponent za 125 hodin.
a) Je známo, že průměr poruch za 100 hodin je 8, proto se za 25 hodin očekává čtvrtina poruch, tj. 2 poruchy. Toto bude parametr μ.
Je požadována pravděpodobnost selhání 1 komponenty, náhodná proměnná je „komponenty, které selhají před 25 hodinami“ a její hodnota je y = 1. Nahrazením pravděpodobnostní funkce:
Otázkou však je, jak je pravděpodobné, že selžou méně než dvě složky za 50 hodin, ne že by přesně 2 komponenty selhaly za 50 hodin, proto musíme přidat pravděpodobnosti, že:
-Žádné selhání
-Selhání pouze 1
P (selhání méně než 2 komponent) = P (0) + P (1)
P (selhání méně než 2 složek) = 0,0183 + 0,0732 = 0.0915
c) Že selžou alespoň 3 komponenty za 125 hodin, znamená, že 3, 4, 5 nebo více může za tu dobu selhat.
Pravděpodobnost, že k tomu dojde alespoň jedna z několika událostí se rovná 1, minus pravděpodobnost, že k žádné z událostí nedojde.
-Požadovanou událostí je, že 3 nebo více komponent selže za 125 hodin
-Pokud k události nedojde, znamená to, že selžou méně než 3 komponenty, jejichž pravděpodobnost je: P (0) + P (1) + P (2)
Parametr μ distribuce je v tomto případě:
μ = 8 + 2 = 10 poruch za 125 hodin.
P (selhání 3 nebo více komponent) = 1- P (0) - P (1) - P (2) =
Zatím žádné komentáře