Vzorec rovnic druhého stupně, jejich řešení, příklady, cvičení

The kvadratické nebo kvadratické rovnice a neznámý mají podobu sekera^dva + bx + c = 0. Kde a ≠ 0, protože kdyby to bylo 0, rovnice by se transformovala do lineární rovnice a koeficienty a, b a c jsou reálná čísla.

Neznámou, kterou je třeba určit, je hodnota x. Například rovnice 3x^dva - 5x + 2 = 0 je úplná kvadratická rovnice.

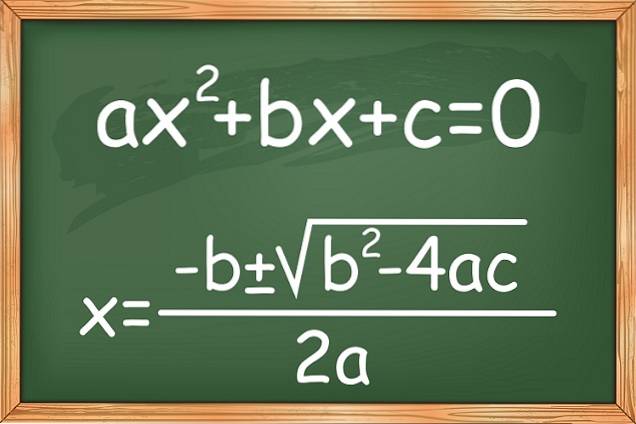
Existují také varianty známé jako neúplné rovnice druhého stupně, kterým chybí jakýkoli výraz, kromě výrazu z sekera^dva. Zde jsou nějaké příklady:

X^dva - 25 = 0

3x^dva - 5x = 0

Al Juarismi, slavný arabský matematik starověku, popsal ve svých pracích různé typy rovnic prvního a druhého stupně, ale pouze s kladnými koeficienty. Byl to však francouzský matematik Francois Viete, kdo jako první zavedl písmena symbolizující veličiny a navrhl řešení pomocí vzorce rezolutní:

Toto je obecný vzorec, který umožňuje řešení kvadratické rovnice, hledání jejích kořenů nebo nul, i když řešení nejsou reálná. Existují i ​​jiné způsoby, jak je vyřešit.

Rejstřík článků

• 1 Jak řešit kvadratické rovnice?
  • 1.1 Rozlišení pomocí factoringu
  • 1.2 Grafická metoda
  • 1.3 Rozlišení pomocí vědecké kalkulačky
  • 1.4 Diskriminující kvadratické rovnice
• 2 Příklady jednoduchých kvadratických rovnic
  • 2.1 Rovnice tvaru x2 + mx + n = 0
  • 2.2 Neúplná rovnice tvaru ax2 + c = 0
  • 2.3 Neúplná rovnice tvaru ax2 + bx = 0
  • 2.4 Rovnice se jmenovatelem
  • 2.5 Rovnice vyššího řádu, které se stanou kvadratickými
• 3 jednoduchá řešená cvičení
  • 3.1 - Cvičení 1
  • 3.2 - Cvičení 2
  • 3.3 - Cvičení 3
• 4 Odkazy

Jak řešit kvadratické rovnice?

Rovnice druhého stupně lze vyřešit výše uvedeným vzorcem a existují také další algebraické postupy, které mohou dát výsledek v některých rovnicích.

Na začátku navrhneme rovnici navrženou vzorcem, což je platná metoda pro jakoukoli kvadratickou rovnici s jednou neznámou:

3x^dva - 5x + 2 = 0

Abychom vzorec používali správně, upozorňujeme, že:

• na je koeficient členu s x^dva
• b je koeficient lineárního členu
• C je nezávislý termín.

Budeme je identifikovat ze stejné rovnice:

a = 3

b = -5

c = 2

Je třeba vzít v úvahu znaménko doprovázející koeficient. Nyní tyto hodnoty dosadíme do vzorce:

V čitateli je symbol „plus - minus“ ±, což znamená, že veličinu s odmocninou lze brát jako kladnou i zápornou. Kvadratická rovnice má nanejvýš dvě reálná řešení a tento symbol to bere v úvahu.

Říkejme x₁ a x_dva k těmto dvěma řešením, pak:

X₁ = (5 + 1) / 6 = 1

X_dva = (5-1) / 6 = 4/6 = 2/3

Rozlišení pomocí factoringu

Některé rovnice druhého stupně sestávají z trinomiálů, které lze snadno započítat. Pokud ano, je tato metoda mnohem rychlejší. Uvažujme rovnici:

X^dva + 7x - 18 = 0

Faktorizace má tuto formu:

(x +) ⋅ (x -)

Mezery jsou vyplněny dvěma čísly, která při vynásobení dávají 18 a při odečtení dávají 7. Znaky v závorkách se volí pomocí tohoto kritéria:

-V první závorce je znaménko umístěno mezi prvním a druhým členem.

-A v druhé závorce je produkt známek, které jsou vidět.

Pokud jde o čísla, v tomto případě se snadno skórují: jsou to 9 a 2. Největší je vždy umístěn v první závorce, například takto:

X^dva + 7x - 18 = (x + 9). (x - 2)

Čtenář si může pomocí distributivní vlastnosti ověřit, že při vývoji produktu pravé strany rovnosti je získána trinomie levé. Nyní je rovnice přepsána:

(x + 9) ⋅ (x - 2) = 0

Aby byla rovnost splněna, stačí, aby jeden ze dvou faktorů byl nulový. Takže v první musíte udělat x₁ = -9 nebo se může stát, že druhý faktor zmizí, v takovém případě x_dva = 2. Toto jsou řešení rovnice.

Grafická metoda

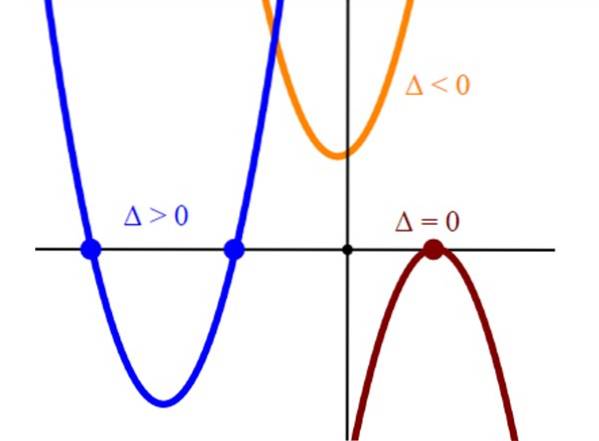
Kořeny nebo řešení kvadratické rovnice odpovídají průsečíkům paraboly y = sekera^dva + bx + c s vodorovnou osou nebo osou x. Takže při grafu odpovídající paraboly najdeme řešení kvadratické rovnice tak, že y = 0.

Řezy paraboly s vodorovnou osou představují řešení rovnice sekera^dva + bx + c = 0. Parabola, která pouze ořezává vodorovnou osu v jednom bodě, má jeden kořen a vždy to bude vrchol paraboly.

A konečně, pokud parabola neřízne vodorovnou osu, odpovídající rovnici sekera^dva + bx + c = 0 chybí skutečná řešení.

Ruční vytváření grafů může být pracné, ale s využitím programů, které grafují online, je to velmi jednoduché.

Rozlišení pomocí vědecké kalkulačky

Mnoho modelů vědeckých kalkulaček má možnost řešení kvadratických rovnic (a také jiných typů rovnic). Chcete-li to zjistit, musíte zkontrolovat nabídku.

Jakmile je vybrána kvadratická rovnice jedné neznámé možnosti, nabídka požádá o zadání hodnot koeficientů a, bac a vrátí reálná řešení, pokud existují. A existují také modely vědeckých kalkulaček, které pracují se složitými čísly a nabízejí tato řešení.

Diskriminující kvadratické rovnice

Chcete-li zjistit, zda rovnice má skutečná řešení nebo ne, a kolik jich je, aniž byste museli nejprve řešit, je diskriminační Δ definována jako množství pod druhou odmocninou:

Δ = b^dva - 4ac

Podle znaménka diskriminujícího je známo, kolik řešení má rovnice podle tohoto kritéria:

-Dvě skutečná řešení: Δ> 0

-Skutečné řešení (nebo dvě identická řešení): Δ = 0

-Žádné skutečné řešení: Δ  < 0

Například kolik řešení má kvadratická rovnice -7x^dva +12x + 64 = 0? Identifikujeme koeficienty:

a = -7

b = 12

c = 64

Δ = b^dva - 4ac = 12^dva - 4x (-7) x 64 = 144 + 1792 = 1936> 0

Rovnice má dvě řešení. Nyní se podívejme na tento další:

X^dva - 6x + 9 = 0

a = 1

b = -6

c = 9

Δ = (-6)^dva - 4 x 1 x 9 = 36-36 = 0

Jedná se o rovnici s jediným řešením nebo se dvěma stejnými řešeními.

Příklady jednoduchých kvadratických rovnic

Na začátku jsme řekli, že rovnice druhého stupně mohou být úplné, pokud je trinomiální, a neúplné, pokud chybí lineární člen nebo nezávislý člen. Nyní se podívejme na některé konkrétní typy:

Rovnice tvaru x^dva + mx + n = 0

V tomto případě a = 1 a vzorec se sníží na:

U tohoto typu rovnice a vždy v závislosti na zbývajících koeficientech může metoda factoringu fungovat dobře, jak jsme viděli v předchozí části.

Neúplná rovnice tvarové sekery^dva + c = 0

Řešení, pokud existuje, má formu:

Skutečné řešení existuje, když a nebo c mají záporné znaménko, ale pokud mají dva výrazy stejné znaménko, bude řešení imaginární.

Neúplná rovnice tvarové sekery^dva + bx = 0

Tato rovnice je rychle vyřešena pomocí factoringu, protože x je společný faktor v obou termínech. Jedno z řešení je vždy x = 0, druhé se nachází takto:

sekera^dva + bx = 0

x (ax + b) = 0

ax + b = 0 → x = -b / a

Podívejme se na příklad níže. Vytřídit:

X^dva - 5x = 0

x (x - 5) = 0

Proto x₁ = 0 a x_dva = 5

Rovnice se jmenovatelem

Existují různé rovnice racionálního typu, ve kterých může být neznámé přítomno jak v čitateli, tak ve jmenovateli, nebo dokonce pouze ve druhém, a které se pomocí algebraických manipulací redukují na kvadratické rovnice.

Způsob, jak je vyřešit, je znásobit obě strany rovnosti nejmenším společným násobkem nebo m.c.m jmenovatelů a poté uspořádat termíny. Například:

Rovnice vyššího řádu, které se stanou kvadratickými

Existují rovnice vyššího řádu, které lze řešit, jako by byly kvadratické pomocí změny proměnné, například tato rovnice bi-square:

X⁴ - 10x^dva + 9 = 0

Nechť x^dva = u, pak se rovnice stává:

nebo^dva - 10u + 9 = 0

Tato rovnice je rychle vyřešena factoringem, nalezením dvou čísel, která se vynásobí 9 a přidá 10. Tato čísla jsou 9 a 1:

(u - 9). (u - 1) = 0

Řešení této rovnice jsou tedy u₁ = 9 a u_dva = 1. Nyní vrátíme změnu:

X^dva = 9 → x₁ = 3 a x_dva = -3

X^dva = 1 → x₁ = 1 a x_dva = -1

Původní rovnice je řádu 4, proto má alespoň 4 kořeny. Ten v příkladu je -3, -1, 1 a 3.

Jednoduchá řešená cvičení

- Cvičení 1

Vyřešte následující kvadratickou rovnici s neznámým ve jmenovateli:

Nejméně běžný násobek je x (x + 2) a musíte znásobit všechny výrazy:

Ekvivalentní výraz zůstává:

5x (x + 2) - x = x (x + 2)

Vyvíjíme:

5x^dva + 10x - x = x^dva + 2x

Všechny výrazy jsou transponovány nalevo od rovnosti a vpravo necháme 0:

5x^dva + 10x - x - x^dva - 2x = 0

4x^dva - 7x = 0

Faktorujeme, protože jde o neúplnou rovnici:

x (4x - 7) = 0

Jedno z řešení je x = 0, druhé je:

4x = 7

x = 7/4

- Cvičení 2

Najděte řešení kvadratických rovnic:

a) -7x^dva +12x + 64 = 0

b) x^dva - 6x + 9 = 0

Řešení

Z této rovnice víme determinant Δ, protože byl vypočítán jako příklad dříve, takže ho využijeme a vyjádříme řešení takto:

X₁ = (-12 + 44) / -14 = - (32/14) = - (16/7)

X_dva = (-12 - 44) / -14 = 4

Řešení b

Čtvercový trojčlen x^dva - 6x + 9 je factorable, protože se jedná o dokonalý čtvercový trinomial:

X^dva - 6x + 9 = (x-3)^dva = 0

Řešení této rovnice je x = 3.

- Cvičení 3

Jaká je rovnice, jejíž řešení jsou 3 a 4?

Řešení

Faktorový výraz je:

(x - 3) ⋅ (x - 4) = 0

Uplatnění distribučního majetku:

X^dva - 4x -3x + 12 = 0

Tyto dva centrální termíny jsou podobné a lze je omezit, takže:

X^dva - 7x + 12 = 0

Reference

1. Baldor. 1977. Elementární algebra. Venezuelské kulturní edice.
2. Hoffman, J. Výběr témat matematiky. Svazek 2.
3. Jiménez, R. 2008. Algebra. Hala Prentice.
4. Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Edice. Cengage Learning.
5. Zapata, F. 4 způsoby řešení kvadratické rovnice. Obnoveno z: francesphysics.blogspot.com.
6. Zill, D. 1984. Algebra a trigonometrie. Mcgraw kopec.