The elektromagnetická energie Je to ten, který se šíří elektromagnetickými vlnami (EM). Příkladem toho je sluneční světlo vyzařující teplo, proud odebíraný z elektrické zásuvky a ten, který mají rentgenové paprsky k produkci rentgenových paprsků.
Stejně jako zvukové vlny, když vibrují ušní bubínek, jsou elektromagnetické vlny schopné přenášet energii, kterou lze později převést na teplo, elektrické proudy nebo různé signály..
Elektromagnetická energie se šíří jak v materiálovém médiu, tak ve vakuu, vždy ve formě příčné vlny a její využití není nic nového. Sluneční světlo je nejstarším známým a prvotním zdrojem elektromagnetické energie, ale používání elektřiny je o něco novější.
Teprve v roce 1891 Edison Company zprovoznil první elektrickou instalaci v Bílém domě ve Washingtonu DC. A to jako doplněk plynových světel, která se v té době používala, protože zpočátku byla v jejich používání velká skepse..
Pravdou je, že i na nejvzdálenějších místech a bez elektrického vedení elektromagnetická energie, která neustále přichází z vesmíru, neustále udržuje dynamiku toho, čemu říkáme náš domov ve vesmíru..
Rejstřík článků
Elektromagnetické vlny jsou příčné vlny, ve kterých je elektrické pole A a magnetické pole B jsou na sebe kolmé, směr šíření vlny je kolmý na pole.
Všechny vlny se vyznačují svou frekvencí. Je to široký frekvenční rozsah EM vln, který jim dává univerzálnost při transformaci jejich energie, která je úměrná frekvenci.
Obrázek 2 ukazuje elektromagnetickou vlnu, v ní elektrické pole A modře osciluje v rovině z y, magnetické pole B červeně to dělá v letadle xy, zatímco rychlost vlny je směrována podél osy +Y, podle zobrazeného souřadnicového systému.
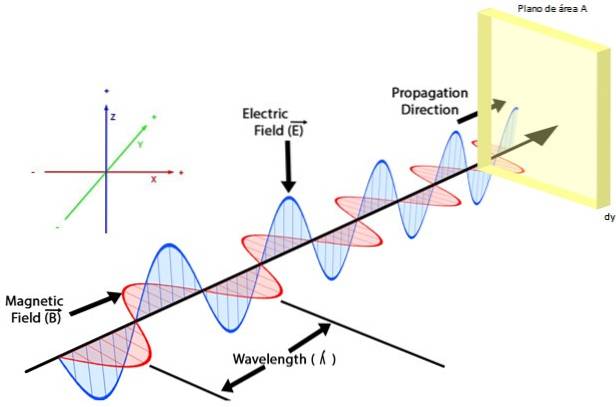
Pokud je povrch vložen do dráhy obou vln, řekněme rovinu plochy NA a tloušťka dy, tak, že je kolmá na rychlost vlny, tok elektromagnetické energie na jednotku plochy, označený S, je popsán prostřednictvím poyntingový vektor:
S = (1 / μnebo) A × B
μnebo je propustnost vakua (μnebo = 4π .10-7 Tesla. metr / ampér), konstanta související s lehkostí, kterou médium dává elektromagnetické vlně k pohybu.
Poyntingův vektor představil anglický astrofyzik John Henry Poynting v roce 1884, průkopník ve studiu energie elektrických a magnetických polí..
Nyní je třeba vzít v úvahu, že energie je skalární S je to vektor.
Pamatujeme si, že výkon je energie dodaná za jednotku času, pak modul S označuje okamžitý výkon na jednotku plochy ve směru šíření elektromagnetických vln (rychlost přenosu energie).
Od té doby A Y B jsou na sebe kolmé, modul o A X B je to jen EB a okamžitý výkon (skalární) je jako:
S = (1 / μnebo) EB
Je snadné zkontrolovat, že jednotky S jsou Watt / mdva v mezinárodním systému.
Stále je toho víc. Veličiny polí A Y B jsou navzájem spojené rychlostí světla C. Ve skutečnosti se elektromagnetické vlny ve vakuu šíří tak rychle. Tento vztah je:
E = cB
Dosazením tohoto vztahu v S získáme:
S = (1 / μnebo.ESdva
Poyntingův vektor se mění s časem sinusovým způsobem, takže předchozí výraz je jeho maximální hodnota, protože energie dodávaná elektromagnetickou vlnou také osciluje, stejně jako pole. Frekvence oscilace je samozřejmě velmi velká, proto ji například není možné detekovat ve viditelném světle.
Z mnoha použití, která jsme již zmínili pro elektromagnetickou energii, jsou zde uvedena dvě, která se používají nepřetržitě v mnoha aplikacích:
Antény jsou všude a vyplňují prostor elektromagnetickými vlnami. Existují vysílače, které transformují elektrické signály například na rádiové vlny nebo mikrovlnné záření. A existují přijímače, které pracují opačně: shromažďují vlny a převádějí je na elektrické signály.
Podívejme se, jak vytvořit elektromagnetický signál, který se šíří ve vesmíru, z elektrického dipólu. Dipól se skládá ze dvou elektrických nábojů stejné velikosti a opačných znaků, oddělených malou vzdáleností.
Na následujícím obrázku je elektrické pole A když je zátěž + nahoru (obrázek vlevo). A ukazuje dolů v zobrazeném bodě.
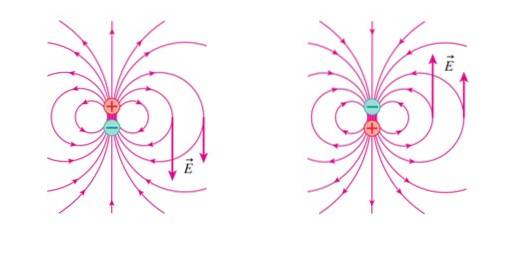
Na obrázku 3 vpravo dipól změnil polohu a nyní A ukazuje nahoru. Zopakujme tuto změnu mnohokrát a velmi rychle, řekněme s frekvencí F. Tím se vytvoří pole A proměnná v čase vede k magnetickému poli B, také variabilní a jehož tvar je sinusový (viz obrázek 4 a příklad 1 níže).
A protože Faradayův zákon zajišťuje, že magnetické pole B proměnná v čase vede k vzniku elektrického pole, protože se ukazuje, že kmitáním dipólu již má elektromagnetické pole schopné se šířit v médiu.
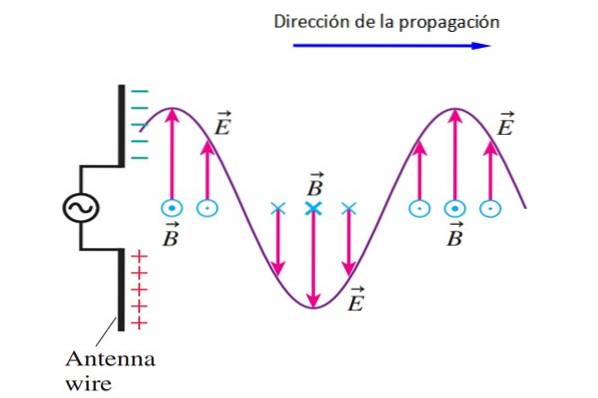
cítím to B body střídavě na obrazovku nebo z obrazovky (vždy kolmo na A).
Kondenzátory slouží k ukládání elektrického náboje, a tedy i elektrické energie. Jsou součástí mnoha zařízení: motory, rádiové a televizní obvody, systémy osvětlení automobilů a mnoho dalšího.
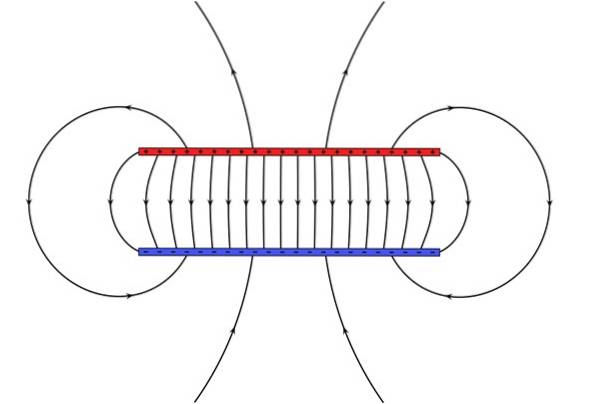
Kondenzátory se skládají ze dvou vodičů oddělených malou vzdáleností. Každý z nich dostane náboj stejné velikosti a opačného znaménka, čímž vytvoří elektrické pole v prostoru mezi dvěma vodiči. Geometrie se může měnit, což je dobře známá geometrie plochého paralelního deskového kondenzátoru.
Energie uložená v kondenzátoru pochází z práce, která byla provedena k jeho nabití a která sloužila k vytvoření elektrického pole v něm. Zavedením dielektrického materiálu mezi desky se zvyšuje kapacita kondenzátoru a tím i energie, kterou může akumulovat.
Kondenzátor kapacity C a zpočátku vybitý, který je nabíjen baterií, která dodává napětí V, dokud nedosáhne nabití Q, ukládá energii U danou:
U = ½ (Qdva/ C) = ½ QV = ½ CVdva
Dříve se říkalo, že velikost Poyntingova vektoru je ekvivalentní s výkonem, který vlna dodává na každý metr čtvereční plochy, a že také, protože vektor je časově závislý, jeho hodnota oscilovala až na maximum S = S = (1 / μnebo.ESdva.
Průměrná hodnota S v jednom cyklu vlny je snadno měřitelná a je indikátorem energie vlny. Tato hodnota je známá jako intenzita vln a počítá se tímto způsobem:
I = Spolovina = S = (1 / μnebo.ESdvapolovina
Elektromagnetická vlna je reprezentována sinusovou funkcí:
E = Enebo hřích (kx - ωt)
Kde Anebo je amplituda vlny, k číslo vlny a ω úhlová frekvence. Pak:
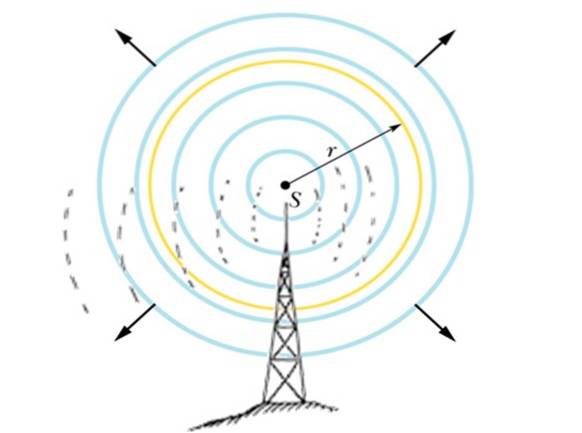
Existuje rozhlasová stanice, která vysílá signál o výkonu 10 kW a frekvenci 100 MHz, který se šíří sférickým způsobem, jako na obrázku výše..
Najděte: a) amplitudu elektrického a magnetického pole v bodě vzdáleném 1 km od antény ab) celkovou elektromagnetickou energii dopadající na čtvercový list se stranou 10 cm za dobu 5 minut.
Údaje jsou:
Rychlost světla ve vakuu: c = 300 000 km / s
Vakuová propustnost: μnebo = 4π .10-7 T.m / A (Tesla. Meter / ampér)
Rovnice uvedená v příkladu 1 se používá k nalezení intenzity elektromagnetické vlny, ale nejprve musí být hodnoty vyjádřeny v mezinárodním systému:
10 kW = 10 000 W.
100 MHz = 100 x 106 Hz
Tyto hodnoty jsou v rovnici okamžitě nahrazeny intenzitou, protože jde o zdroj, který vyzařuje všude stejné (zdroj izotropní):
%5E%7B2%7Dm%5E%7B2%7D%7D=7.96x10%5E%7B-4%7D%5C:&space;W/m%5E%7B2%7D)
Dříve se říkalo, že veličiny A Y B byly spojeny rychlostí světla:
E = cB
B = (0,775 / 300 000 000) T = 2,58 x 10-9 T
Spolovina je výkon na jednotku plochy a zase výkon je energie na jednotku času. Násobení Spolovina Podle plochy desky a doby expozice se získá požadovaný výsledek:
5 minut = 300 sekund
Plocha = (10/100)dva mdva = 0,01 mdva.
U = 0,775 x 300 x 0,01 Joulů = 2,325 Joulů.
Zatím žádné komentáře