The standardní chyba odhadu měří odchylku v hodnotě vzorku populace. To znamená, že standardní chyba odhadu měří možné odchylky střední hodnoty vzorku vzhledem ke skutečné hodnotě střední hodnoty populace..
Například pokud chcete znát průměrný věk populace země (průměr obyvatel), vezmete malou skupinu obyvatel, kterou budeme nazývat „vzorek“. Z toho se získá průměrný věk (průměr vzorku) a předpokládá se, že populace má tento průměrný věk se standardní chybou odhadu, která se víceméně liší..
Je třeba poznamenat, že je důležité nezaměňovat standardní odchylku se standardní chybou a se standardní chybou odhadu:
1 - Směrodatná odchylka je měřítkem rozptylu dat; to znamená, že se jedná o měřítko variability populace.
2 - Standardní chyba je míra variability vzorku vypočítaná na základě směrodatné odchylky populace.
3- Standardní chyba odhadu je míra chyby, ke které dojde, když vezmeme průměr vzorku jako odhad průměru populace.
Rejstřík článků
Standardní chybu odhadu lze vypočítat pro všechna měření, která se získají ve vzorcích (například standardní chyba odhadu střední hodnoty nebo standardní chyba odhadu směrodatné odchylky) a měří chybu, ke které dochází při odhadu skutečné populace změřit z jeho hodnoty vzorku
Ze standardní chyby odhadu je sestaven interval spolehlivosti odpovídající míry.
Obecná struktura vzorce pro standardní chybu odhadu je následující:
Standardní chyba odhadu = ± Koeficient spolehlivosti * Standardní chyba
Koeficient spolehlivosti = mezní hodnota statistiky vzorku nebo rozdělení vzorkování (normální nebo Gaussův zvon, Studentův t, mimo jiné) pro daný interval pravděpodobnosti.
Standardní chyba = směrodatná odchylka populace vydělená druhou odmocninou velikosti vzorku.
Koeficient spolehlivosti označuje počet standardních chyb, které jste ochotni přidat a odečíst k měření, abyste měli určitou úroveň spolehlivosti ve výsledcích..
Předpokládejme, že se snažíte odhadnout podíl lidí v populaci, kteří mají chování A, a chcete mít 95% důvěru ve své výsledky..
Odebírá se vzorek n lidí a stanoví se podíl vzorku p a jeho doplněk q.
Standardní chyba odhadu (SEE) = ± Koeficient spolehlivosti * Standardní chyba
Koeficient spolehlivosti = z = 1,96.
Standardní chyba = druhá odmocnina poměru mezi součinem podílu vzorku a jeho doplňku a velikostí vzorku n.
Ze standardní chyby odhadu je stanoven interval, ve kterém se očekává podíl populace, nebo podíl vzorku jiných vzorků, které lze z této populace vytvořit, s 95% úrovní spolehlivosti:
p - EEE ≤ Populační podíl ≤ p + EEE
1 - Předpokládejme, že se snažíte odhadnout podíl lidí v populaci, kteří upřednostňují obohacené mléčné složení, a chcete mít 95% důvěru ve své výsledky..
Odebere se vzorek 800 lidí a 560 osob ve vzorku se rozhodne, že dává přednost složení obohaceného mléka. Určete interval, ve kterém lze očekávat podíl populace a podíl dalších vzorků, které lze z populace odebrat, s 95% spolehlivostí
a) Vypočítáme podíl vzorku p a jeho doplněk:
p = 560/800 = 0,70
q = 1 - p = 1 - 0,70 = 0,30
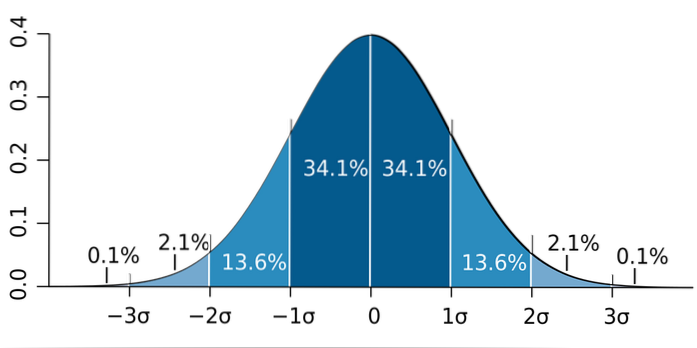
b) Je známo, že podíl se blíží normálnímu rozdělení na velké vzorky (větší než 30). Poté se použije takzvané pravidlo 68 - 95 - 99,7 a my musíme:
Koeficient spolehlivosti = z = 1,96
Standardní chyba = √ (p * q / n)
Standardní chyba odhadu (SEE) = ± (1,96) * √ (0,70) * (0,30) / 800) = ± 0,0318
c) Ze standardní chyby odhadu se stanoví interval, ve kterém se očekává podíl populace s 95% úrovní spolehlivosti:
0,70 - 0,0318 ≤ Podíl populace ≤ 0,70 + 0,0318
0,6682 ≤ Podíl populace ≤ 0,7318
Lze očekávat, že 70% podíl vzorku se změní až o 3,18 procentního bodu, pokud si vezmete jiný vzorek 800 jedinců nebo pokud je skutečný podíl populace mezi 70 - 3,18 = 66,82% a 70 + 3,18 = 73,18%.
2 - Vezmeme od Spiegela a Stephense, 2008, následující případovou studii:
Náhodný vzorek 50 známek byl odebrán z celkových známek matematiky studentů prvního ročníku univerzity, přičemž zjištěný průměr byl 75 bodů a směrodatná odchylka 10 bodů. Jaké jsou 95% limity spolehlivosti pro odhad střední matematické známky??
a) Pojďme vypočítat standardní chybu odhadu:
95% koeficient spolehlivosti = z = 1,96
Standardní chyba = s / √n
Standardní chyba odhadu (SEE) = ± (1,96) * (10√50) = ± 2,7718
b) Ze standardní chyby odhadu se stanoví interval, ve kterém se očekává průměr populace nebo průměr jiného vzorku velikosti 50, s 95% úrovní spolehlivosti:
50 - 2,7718 ≤ Průměr populace ≤ 50 + 2,7718
47,2282 ≤ Průměr populace ≤ 52,77718
c) Lze očekávat, že se průměr vzorku změní až o 2,7718 bodu, pokud je vybrán jiný vzorek 50 známek nebo pokud je skutečný průměr matematické známky z populace univerzity mezi 47,2282 bodů a 52,77718 bodů.
Zatím žádné komentáře