
Smykový stres, jak se počítá a řeší cvičení
Je znám jako pevnost ve smyku Výsledek působení dvou sil rovnoběžně s povrchem a v opačném směru. Tímto způsobem lze objekt rozdělit na dvě části, díky čemuž se sekce posouvají přes sebe..
Přímé smykové síly jsou denně aplikovány na textilie, papíry nebo kovy, vyvíjené nůžkami, gilotinami nebo nůžkami. Objevují se také ve strukturách, jako jsou šrouby nebo šrouby, hmoždinky, nosníky, klíny a svary..

Je nutné objasnit, že není vždy zamýšleno řezat nebo řezat, ale smykové napětí má tendenci deformovat předmět, na který je aplikováno; paprsky vystavené smykovému namáhání mají proto tendenci se prohýbat pod svou vlastní hmotností. Následující příklady objasňují věc.
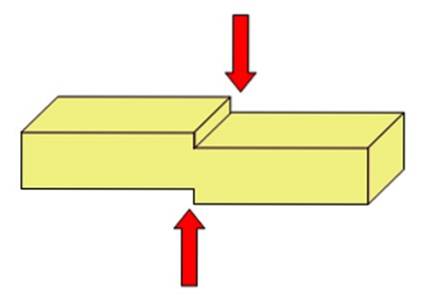
Obrázek 2 ukazuje jednoduchý diagram ilustrující výše uvedené. Je to objekt, na který působí dvě síly v opačných směrech. Existuje imaginární rovina řezu (není nakreslena) a síly působí po jedné na každé straně roviny a lišta se rozřízne na dvě.
V případě nůžek: každá čepel nebo hrana působí silou na průřez (kruhový) řezaného předmětu a také jej rozděluje na dvě části, jako je struna na obrázku 1.
Rejstřík článků
- 1 Smykové napětí může způsobit deformaci
- 2 Jak se vypočítává smykové napětí??
- 3 Smykové napětí a deformace
- 4 Vyřešená cvičení
- 4.1 - Cvičení 1
- 4.2 - Cvičení 2
- 5 Reference
Smykové napětí může způsobit deformaci
Můžete zkusit vyvinout řeznou sílu posunutím ruky přes obal uzavřené knihy. Druhé víko musí zůstat upevněné na stole, čehož lze dosáhnout podepřením volné ruky tak, aby se nehýbala. Kniha se touto akcí trochu deformuje, jak je uvedeno na následujícím obrázku:
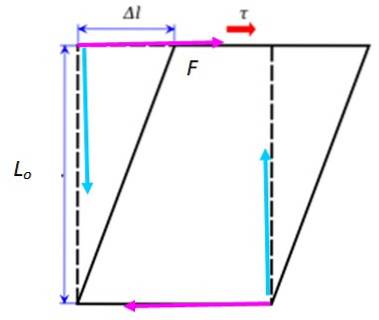
Pokud je tato situace pečlivě analyzována, obě síly již byly zmíněny, ale tentokrát byly použity horizontálněve fuchsii). Jedním z nich je vaše ruka na jedné straně a druhá je aplikována povrchem stolu na opačné straně knihy, který je připevněn.
Kniha se neotáčí, i když by tyto síly mohly způsobit čistý točivý moment nebo moment. Aby se tomu zabránilo, existují další dvě svislé síly (v tyrkysové barvě); ten aplikovaný druhou rukou a normální vyvíjený stolem, jehož čistý moment působí v opačném směru a brání rotačnímu pohybu.
Jak se počítá smykové napětí?
Střižná napětí se objevují i uvnitř lidského těla, protože cirkulující krev neustále vyvíjí tangenciální síly na vnitřní stranu cév, což způsobuje malé deformace ve stěnách..
Vaše úvahy jsou důležité při určování pravděpodobnosti selhání struktury. U smykových sil se nezohledňuje pouze síla, ale také oblast, na kterou působí.
To je okamžitě pochopitelné tím, že se vezmou dvě válcové tyče stejné délky, vyrobené ze stejného materiálu, ale různé tloušťky, a vystaví je rostoucímu napětí, dokud se nerozbijí..
Je zřejmé, že potřebné síly budou zcela odlišné, protože jedna tyč je tenčí než druhá; úsilí však bude stejné.
Smykové napětí je označeno řeckým písmenem τ (tau) a vypočítá se jako podíl mezi velikostí aplikované síly F a okolí NA povrchu, na který působí:
τprůměrný= F / A
Takto vypočítané úsilí vyvíjí průměrnou sílu na dotyčný povrch, protože tato síla nepůsobí na jediný bod na povrchu, ale je rozložena na celý tento povrch a není rovnoměrná. Rozložení však může být reprezentováno výslednou silou působící na určitý bod.
Rozměry smykového napětí jsou síla na povrchu. V jednotkách mezinárodního systému odpovídají newton / metr čtvereční, jednotce zvané Pascal a zkráceně Pa.
Jsou to stejné jednotky tlaku, proto jednotky anglického systému jako libra síla / stopa dva a libra síla / palecdva jsou také vhodné.
Smykové napětí a deformace
V mnoha situacích je velikost smykového napětí úměrná napětí způsobenému v objektu, jako v předchozí ukázkové knize, která se vrátí do původních rozměrů, jakmile je ruka odstraněna. V tom případě:
Pevnost ve smyku ∝ Deformace jednotky
Konstanta proporcionality je v tomto případě modul smyku, modul tuhosti nebo modul smyku (G):
Smykové napětí = Smykový modul x Jednotkové přetvoření
τ = G. γ
S γ = ΔL / Lnebo, kde ΔL je rozdíl mezi konečnou a počáteční délkou. Kombinací uvedených rovnic lze nalézt výraz pro přetvoření způsobené stresem:
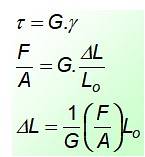
Hodnota konstanty G Nachází se v tabulkách a jeho jednotky jsou stejné jako u napětí, protože napětí je bezrozměrné. Téměř vždy hodnota G je polovina nebo třetina hodnoty A, modul pružnosti.
Ve skutečnosti jsou spojeny výrazem:
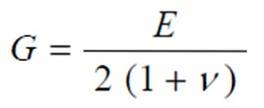
Kde ν je Poissonův modul, další elastická konstanta materiálu, jehož hodnota je mezi 0 a ½. Právě z tohoto důvodu je G zase mezi E / 3 a E / 2.
Vyřešená cvičení
-Cvičení 1
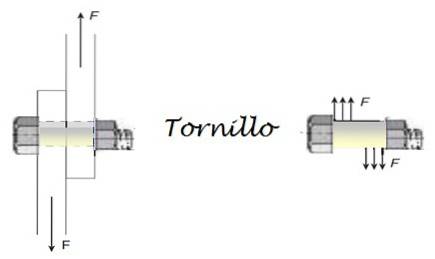
Ke spojení dvou železných desek se používá ocelový šroub, který musí odolat smykovým silám až 3 200 N. Jaký je minimální průměr šroubu, pokud je bezpečnostní faktor 6,0? Je známo, že materiál pojme až 170 x 106 N / mdva.
Řešení
Smykové napětí, kterému je šroub vystaven, pochází ze sil uvedených na obrázku níže. Bezpečnostní faktor je bezrozměrná veličina a souvisí s maximálním povoleným napětím:
Smykové napětí = F / A = Maximální dovolené napětí / součinitel bezpečnosti
Proto oblast je:
A = F x bezpečnostní faktor / smykové napětí = 3200 x 6/170 x 106 = 0,000113 mdva
Plocha šroubu je dána πDdva/ 4, proto je průměr:
Ddva= 4 x A / π = 0,000144 mdva
D = 0,012 m = 12 mm.
-Cvičení 2
K zabránění otáčení kladky pod tlakem se používá dřevěná hmoždinka nebo hmoždinka T1 Y Tdva, vzhledem k 3palcové ose. Rozměry kolíků jsou znázorněny na obrázku. Najděte velikost smykového napětí na bloku, pokud zobrazené síly působí na kladku:
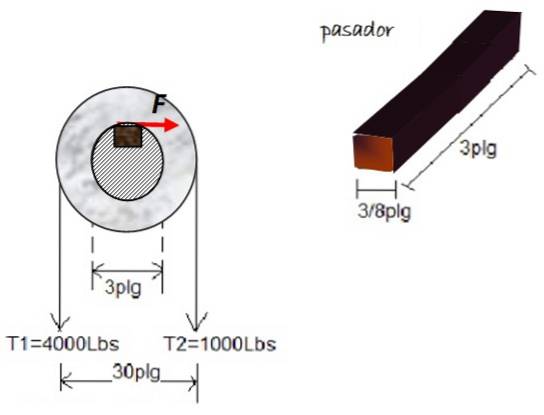
Řešení
T1 vytváří na kladce točivý moment proti směru hodinových ručiček, kterému je přiřazeno kladné znaménko Tdva vytváří točivý moment ve směru hodinových ručiček se záporným znaménkem. Rameno páky měří 15 palců pro každé napnutí. Proto:
Čistý točivý moment = síla 4000 liber. 15 palců - síla 1 000 liber. 15 palců = síla 45 000 liber. palec
Dřevěný blok se nesmí otáčet, proto musí být momenty vzhledem ke středu bloku nulové. F představuje průměrnou sílu na povrchu:
45 000 - F.d = 0
S d = 1,5 palce, Tím pádem:
F x 1,5 = 45 000
F = síla 30 000 liber
Tato síla způsobí smykové napětí velikosti:
τ = F / A = síla 30 000 liber / (3/8 x 3) palecdva = 2,67 x 104 libra síla / palecdva
Reference
- Beer, F. 2010. Mechanika materiálů. 5. Edice. McGraw Hill. 7 - 9.
- Fitzgerald, 1996. Mechanika materiálů. Alfa Omega. 21-23.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6th Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mechanika materiálů. 6.. Edice. Pearson Education. 22-25
- Valera Negrete, J. 2005. Poznámky k obecné fyzice. UNAM. 87-98.
- Wikipedia. Smykové napětí. Obnoveno z: en.wikipedia.org.



Zatím žádné komentáře