A vektorový prostor je neprázdná množina PROTI= nebo, proti, w,…, jejichž prvky jsou vektory. S nimi jsou prováděny některé důležité operace, mezi nimiž vynikají tyto:
- Součet mezi dvěma vektory u + v které výsledky z, který patří do sady PROTI.
- Násobení reálného čísla α vektorem proti: α proti co dává další vektor Y kterému patří PROTI.
K označení vektoru používáme tučné písmo (proti je vektor) a pro skaláry nebo čísla řecká písmena (α je číslo).
Rejstřík článků
Aby mohl být poskytnut vektorový prostor, musí být splněno následujících osm axiomů:
1-přepínatelné: nebo +proti = proti +nebo
2-Transitivita: (nebo + proti) + w = nebo + ( proti + w)
3-Existence nulového vektoru 0 takhle 0 + proti = proti
4-Existence opaku: opak proti to je (-proti) , tak jako proti + (-proti) = 0
5-Distribuce produktu s ohledem na vektorový součet: α ( nebo + proti ) = αnebo +αproti
6-Distribuce produktu vzhledem ke skalárnímu součtu: (α + β)proti = αproti +βproti
7-Asociativita skalárního součinu: α (β proti) = (α β)proti
8 - Číslo 1 je neutrální prvek, protože: 1proti = proti
Vektory v rovině (R²) jsou příkladem vektorového prostoru. Vektor v rovině je geometrický objekt, který má velikost i směr. Je reprezentován orientovaným segmentem, který patří do uvedené roviny a má velikost úměrnou její velikosti.
Součet dvou vektorů v rovině lze definovat jako operaci geometrického překladu druhého vektoru po prvním. Výsledkem součtu je orientovaný segment, který začíná od počátku prvního a dosahuje špičky druhého.
Na obrázku je vidět, že součet v R² je komutativní.
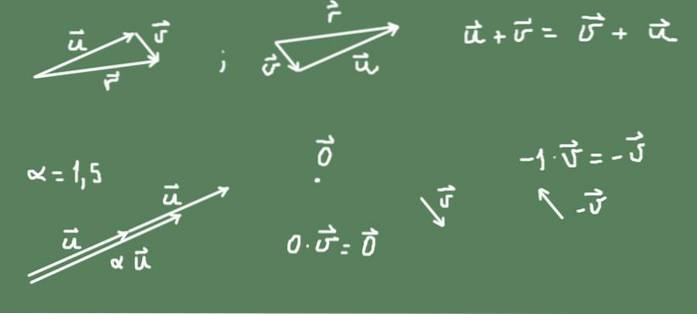
Je také definován součin čísla α a vektoru. Pokud je číslo kladné, je směr původního vektoru zachován a velikost je α krát původní vektor. Pokud je číslo záporné, směr je opačný a velikost výsledného vektoru je absolutní hodnota čísla.
Vektor opačný k jakémukoli vektoru proti to je -proti = (- 1) proti.
Nulový vektor je bod v rovině R² a číslo nula krát vektor vede k nulovému vektoru.
Vše, co je řečeno, je znázorněno na obrázku 2.
Soubor P všech polynomů stupně menšího nebo rovného dvěma, včetně stupně nula, tvoří množinu, která splňuje všechny axiomy vektorového prostoru.
Nechť polynom P (x) = a x² + b x + c a Q (x) = d x² + e x + f
Je definován součet dvou polynomů: P (x) + Q (x) = (a + d) x² + (b + e) x + (c + f)
Součet polynomů patřících do množiny P je komutativní a tranzitivní.
Nulový polynom patřící do množiny P je ten, který má všechny své koeficienty rovné nule:
0 (x) = 0 x² + 0 x + 0
Součet skalárního α polynomem je definován jako: α P (x) = α ∙ a x² + α ∙ b x + α ∙ c
Opačný polynom P (x) je -P (x) = (-1) P (x).
Ze všeho výše uvedeného vyplývá, že množina P ze všech polynomů stupně menšího nebo rovného dvěma je vektorový prostor.
Soubor M všech matic m řádků x n sloupců, jejichž prvky jsou reálná čísla, tvoří skutečný vektorový prostor, s ohledem na operace sčítání matic a součinu čísla maticí.
Sada F spojitých funkcí reálné proměnné tvoří vektorový prostor, protože je možné definovat součet dvou funkcí, násobení skaláru funkcí, nulové funkce a symetrické funkce. Plní také axiomy, které charakterizují vektorový prostor.
Základ vektorového prostoru je definován jako sada lineárně nezávislých vektorů tak, že z jejich lineární kombinace může být generován jakýkoli vektor tohoto vektorového prostoru.
Lineární kombinace dvou nebo více vektorů spočívá v násobení vektorů nějakým skalárem a jejich vektorovém přidání.
Například ve vektorovém prostoru vektorů ve třech rozměrech tvořených R³ se používá kanonický základ definovaný jednotkovými vektory (o velikosti 1) i, j, k.
Kde i = (1, 0, 0); j = (0, 1, 0); k = (0, 0, 1). Jedná se o kartézské nebo kanonické vektory.
Libovolný vektor PROTI patřící k R³ se zapisuje jako PROTI = a i + b j + C k, což je lineární kombinace základních vektorů i, j, k. Skaláry nebo čísla a, b, c jsou známé jako karteziánské složky PROTI.
Rovněž se říká, že základní vektory vektorového prostoru tvoří generátorovou sadu vektorového prostoru.
Dimenze vektorového prostoru je základní číslo vektorového základu pro tento prostor; to znamená počet vektorů, které tvoří uvedenou základnu.
Tento kardinál je maximální počet lineárně nezávislých vektorů tohoto vektorového prostoru a zároveň minimální počet vektorů, které tvoří generátorovou sadu tohoto prostoru.
Základny vektorového prostoru nejsou jedinečné, ale všechny základny stejného vektorového prostoru mají stejnou dimenzi.
Vektorový podprostor S vektorového prostoru V je podmnožinou V, ve které jsou definovány stejné operace jako v V a splňují všechny axiomy vektorového prostoru. Proto bude podprostor S také vektorovým prostorem.
Příkladem vektorového podprostoru jsou vektory, které patří do roviny XY. Tento podprostor je podmnožinou vektorového prostoru dimenzionality většího než sada vektorů patřících do trojrozměrného prostoru XYZ.
Další příklad vektorového podprostoru S1 vektorového prostoru S tvořeného všemi maticemi 2 × 2 se skutečnými prvky je definován níže:
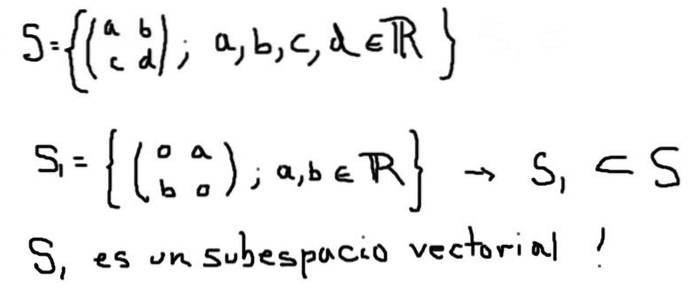
Na druhou stranu, S2 definovaný níže, i když je podmnožinou S, netvoří vektorový podprostor:
Nechť vektory jsou V1= (1, 1, 0); V2= (0, 2, 1) a V3= (0, 0, 3) v R³.
a) Ukažte, že jsou lineárně nezávislé.
b) Ukažte, že tvoří základnu v R³, protože jakoukoli trojici (x, y, z) lze zapsat jako lineární kombinaci V1, V2, V3.
c) Najděte komponenty trojitého PROTI = (-3,5,4) na základně V1, V2, V3.
Kritérium k prokázání lineární nezávislosti spočívá ve stanovení následující sady rovnic v α, β a γ
α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)
V případě, že jediným řešením tohoto systému je α = β = γ = 0, jsou vektory lineárně nezávislé, jinak nejsou.
Pro získání hodnot α, β a γ navrhujeme následující systém rovnic:
α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0
α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0
α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0
První vede k α = 0, druhý α = -2 ∙ β, ale protože α = 0, pak β = 0. Třetí rovnice znamená, že γ = (- 1/3) β, ale protože β = 0, pak γ = 0.
Byl vyvozen závěr, že se jedná o množinu lineárně nezávislých vektorů v R³ .
Nyní zapíšeme trojici (x, y, z) jako lineární kombinaci V1, V2, V3.
(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)
α ∙ 1 + β ∙ 0 + γ ∙ 0 = x
α ∙ 1 + β ∙ 2 + γ ∙ 0 = y
α ∙ 0 + β ∙ 1 + γ ∙ 3 = z
Kde máte:
α = x
α + 2 β = y
β + 3 γ = z
První označuje α = x, druhé β = (y-x) / 2 a třetí γ = (z-y / 2 + x / 2) / 3. Tímto způsobem jsme našli generátory α, β a γ libovolného tripletu R³
Pojďme najít komponenty trojitého PROTI = (-3,5,4) na základně V1, V2, V3.
Nahradíme odpovídající hodnoty ve výrazech nalezených výše pro generátory.
V tomto případě máme: α = -3; β = (5 - (- 3)) / 2 = 4; γ = (4-5/2 + (- 3) / 2) / 3 = 0
To je:
(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)
Podle posledního:
PROTI = -3 V1 + 4 V2 + 0 V3
Došli jsme k závěru, že V1, V2, V3 tvoří základ ve vektorovém prostoru R³ dimenze 3.
Vyjádřete polynom P (t) = t² + 4t -3 jako lineární kombinaci P1 (t) = t² -2t + 5, P2 (t) = 2t² -3t a P3 (t) = t + 3.
P (t) = x P1 (t) + y P2 (t) + z P3 (t)
kde mají být určena čísla x, y, z.
Násobení a seskupování termínů se stejným stupněm v t dává:
t² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)
Což nás vede k následujícímu systému rovnic:
x + 2y = 1
-2x -3y + z = 4
5x + 3z = -3
Řešení tohoto systému rovnic jsou:
x = -3, y = 2, z = 4.
To je:
P (t) = -3 P1 (t) + 2 P2 (t) + 4 P3 (t)
Ukažte, že vektory v1= (1, 0, -1, 2); v2= (1, 1, 0, 1) a v3= (2, 1, -1, 1) z R⁴ jsou lineárně nezávislé.
Lineárně kombinujeme tři vektory v1, v2, v3 a požadujeme, aby kombinace přidala nulový prvek R⁴
na v1 + b v2 + C v3 = 0
A to,
a (1, 0, -1, 2) + b (1, 1, 0, 1) + c (2, 1, -1, 1) = (0, 0, 0, 0)
To nás vede k následujícímu systému rovnic:
a + b + 2 c = 0
b + c = 0
-a - c = 0
2 a + b + c = 0
Odečtením prvního a čtvrtého máme: -a + c = 0, což znamená a = c.
Pokud se ale podíváme na třetí rovnici, máme tu a = -c. Jediný způsob, jak a = c = (- c) platí, je, že c je 0, a proto a bude také 0.
a = c = 0
Pokud dosadíme tento výsledek do první rovnice, usoudíme, že b = 0.
Nakonec a = b = c = 0, aby bylo možné dojít k závěru, že vektory v1, v2 a v3 jsou lineárně nezávislé.
Zatím žádné komentáře