
Doplňkové události, z čeho se skládají, a příklady
The doplňkové akce Jsou definovány jako jakákoli skupina vzájemně se vylučujících událostí, kde je jejich spojení schopné zcela pokrýt prostor vzorku nebo možné případy experimentu (jsou vyčerpávající).
Výsledkem jejich průniku je prázdná množina (∅). Součet pravděpodobností dvou doplňkových událostí se rovná 1. To znamená, že 2 události s touto charakteristikou zcela pokrývají možnost událostí experimentu.

Rejstřík článků
- 1 Co jsou doplňkové akce?
- 2 Co jsou události?
- 3 Co je to plugin?
- 4 Příklady doplňkových akcí
- 5 Doplňková cvičení
- 5.1 Cvičení 1
- 5.2 Cvičení 2
- 5.3 Cvičení 3
- 5.4 Cvičení 4
- 5.5 Cvičení 5
- 6 Reference
Co jsou doplňkové akce?
Velmi užitečným obecným případem pro pochopení tohoto typu události je hod kostkou:
Při definování ukázkového prostoru jsou pojmenovány všechny možné případy, které experiment nabízí. Tato sada je známá jako vesmír.
Ukázkový prostor (S):
S: 1, 2, 3, 4, 5, 6
Možnosti neuvedené ve vzorovém prostoru nejsou součástí možností experimentu. Například nechť vyjde číslo sedm Má pravděpodobnost nula.
Podle cíle experimentování jsou v případě potřeby definovány množiny a podmnožiny. Nastavená notace, která se má použít, je také určena podle cíle nebo parametru, který má být studován:
DO: Nechejte sudé číslo = 2, 4, 6
B: Získejte liché číslo = 1, 3, 5
V tomto případě NA Y B Oni jsou Doplňkové akce. Protože obě sady se vzájemně vylučují (sudé číslo, které je zase liché, nemůže vyjít) a sjednocení těchto sad pokrývá celý ukázkový prostor.
Další možné podmnožiny ve výše uvedeném příkladu jsou:
C : Zanechte prvočíslo = 2, 3, 5
D: x / x Ԑ N ᴧ x ˃ 3 = 4, 5, 6
Soupravy A, B a C. jsou psány v notaci Popisný Y Analytics resp. Pro celek D byla použita algebraická notace, poté byly možné výsledky odpovídající experimentu popsány v notaci Analytics.
V prvním příkladu je pozorováno bytí NA Y B doplňkové akce
DO: Nechejte sudé číslo = 2, 4, 6
B: Získejte liché číslo = 1, 3, 5
Následující axiomy platí:
- A U B = S ; Spojení dvou doplňkové akce se rovná vzorovému prostoru
- A ∩B = ∅; Křižovatka dvou doplňkové akce rovná se prázdná množina
- A '= B ᴧ B' = A; Každá podmnožina se rovná doplňku jejího homologu
- A '∩ A = B' ∩ B = ∅ ; Průnik množiny s jejím doplňkem se rovná prázdné
- A 'U A = B' U B = S; Spojení sady s jejím doplňkem se rovná ukázkovému prostoru
Ve statistikách a pravděpodobnostních studiích doplňkové akce jsou součástí teorie celku a jsou velmi časté u operací prováděných v této oblasti.
Chcete-li se dozvědět více o doplňkové akce, je nutné porozumět určitým pojmům, které je pomáhají koncepčně definovat.
Co jsou události?
Jsou to možnosti a události vyplývající z experimentování, schopné nabídnout výsledky v každé ze svých iterací. The Události generovat data, která mají být zaznamenána jako prvky množin a podmnožin, jsou trendy v těchto údajích důvodem ke studiu pravděpodobnosti.
Příklady událostí jsou:
- Mince špičaté hlavy
- Zápas skončil remízou
- Chemická látka reagovala za 1,73 sekundy
- Rychlost v maximálním bodě byla 30 m / s
- Matrice označila číslo 4
Co je to plugin?
Pokud jde o teorii množin. A Doplněk označuje část prostoru vzorku, kterou je třeba přidat do sady, aby obklopovala její vesmír. Je to všechno, co není součástí celku.
Známým způsobem, jak v teorii množin označit doplněk, je:
Doplněk A
Vennův diagram
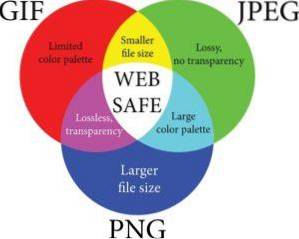
Jedná se o graficky - obsahové analytické schéma, široce používané v matematických operacích zahrnujících množiny, podmnožiny a prvky. Každá sada je reprezentována velkým písmenem a oválnou číslicí (tato vlastnost není v rámci jejího použití povinná), která obsahuje všechny jednotlivé prvky.
The doplňkové akce lze vidět přímo ve Vennových diagramech, protože jeho grafická metoda umožňuje identifikovat doplňky odpovídající každé sadě.
Jednoduše kompletní vizualizace prostředí množiny, vynechání její hraniční a vnitřní struktury, umožňuje definovat doplněk studované množiny..
Příklady doplňkových akcí
Jsou příklady doplňkové akce úspěch a porážka v případě, že rovnost nemůže existovat (baseballový zápas).
Booleovské proměnné jsou doplňkové akce: Pravda nebo nepravda, stejně dobré nebo špatné, uzavřené nebo otevřené, zapnuté nebo vypnuté.
Doplňková cvičení
Cvičení 1
Být S množina vesmíru definovaná všemi přirozenými čísly menšími nebo rovnými deseti.
S: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Následující podskupiny S
H: Přirozená čísla menší než čtyři = 0, 1, 2, 3
J: Násobky po třech = 3, 6, 9
K: Multiples of five = 5
L: 0, 1, 2, 3, 4, 6, 7, 8, 9, 10
M: 0, 1, 2, 4, 5, 7, 8, 10
N: Přirozená čísla větší nebo rovna čtyřem = 4, 5, 6, 7, 8, 9, 10
Rozhodni se:
Kolik doplňkových událostí lze vytvořit spojením dvojic podmnožin S?
Podle definice doplňkové akce Jsou identifikovány páry, které splňují požadavky (vzájemně se vylučují a pokrývají vzorový prostor při připojení). Oni jsou doplňkové akce následující páry podmnožin:
- H a N
- J a M
- L a K.
Cvičení 2
Ukaž to: (M ∩ K) '= L
0, 1, 2, 4, 5, 7, 8, 10 ∩ 5 = 5; Průnik mezi sadami poskytuje společné prvky mezi oběma operantními sadami. Tímto způsobem 5 je jediný společný prvek mezi M Y K..
5 '= 0, 1, 2, 3, 4, 6, 7, 8, 9, 10 = L; Protože L Y K. jsou komplementární, je splněn výše popsaný třetí axiom (Každá podmnožina se rovná doplňku jejího protějšku)
Cvičení 3
Definovat: [(J ∩ H) U N] '
J ∩ H = 3 ; Homologním způsobem k prvnímu kroku předchozího cvičení.
(J ∩ H) U N = 3, 4, 5, 6, 7, 8, 9, 10; Tyto operace jsou známé jako kombinované a obvykle jsou zpracovány Vennovým diagramem.
[(J ∩ H) U N] ' = 0, 1, 2; Je definován doplněk kombinované operace.
Cvičení 4
Ukaž to: [H U N] ∩ [J U M] ∩ [L U K] '= ∅
Složená operace popsaná v složených závorkách se týká průsečíků mezi odbory doplňkových událostí. Tímto způsobem pokračujeme k ověření prvního axiomu (Spojení dvou doplňkové akce rovná se vzorovému prostoru).
[H U N] ∩ [J U M] ∩ [L U K] = S ∩ S ∩ S = S; Spojení a průnik množiny se sebou samým generuje stejnou množinu.
Později; S '= ∅ Podle definice množin.
Cvičení 5
Definujte 4 průniky mezi podmnožinami, jejichž výsledky se liší od prázdné množiny (∅).
- M ∩ N
0, 1, 2, 4, 5, 7, 8, 10 ∩ 4, 5, 6, 7, 8, 9, 10 = 4, 5, 7, 8, 10
- L ∩ H
0, 1, 2, 3, 4, 6, 7, 8, 9, 10 ∩ 0, 1, 2, 3 = 0, 1, 2, 3
- J ∩ N
3, 6, 9 ∩ 4, 5, 6, 7, 8, 9, 10 = 6, 9
Reference
- ÚLOHA STATISTICKÝCH METOD V POČÍTAČOVÉ VĚDĚ A BIOINFORMATICE. Irina Arhipova. Lotyšská zemědělská univerzita, Lotyšsko. [chráněno e-mailem]
- Statistiky a hodnocení důkazů pro forenzní vědce. Druhé vydání. Colin G.G. Aitken. Matematická škola. The University of Edinburgh, UK
- ZÁKLADNÍ TEORIE PRAVDĚPODOBNOSTI, Robert B. Ash. Katedra matematiky. University of Illinois
- Základní STATISTIKA. Desáté vydání. Mario F. Triola. Boston St..
- Matematika a inženýrství v informatice. Christopher J. Van Wyk. Institute for Computer Sciences and Technology. Národní úřad pro standardy. Washington, DC 20234
- Matematika pro informatiku. Eric Lehman. Google Inc..
F Thomson Leighton Katedra matematiky a výpočetní techniky a laboratoře AI, Massachusetts Institute of Technology; Akamai Technologies


Zatím žádné komentáře