
Společný faktor seskupením příkladů termínů, cvičení

The společný faktor seskupením termínů je algebraický postup, který umožňuje psát některé algebraické výrazy ve formě faktorů. K dosažení tohoto cíle je nejprve nutné vhodně seskupit výraz a sledovat, že každá takto vytvořená skupina má ve skutečnosti společný faktor.
Správné použití techniky vyžaduje určitou praxi, ale za krátkou dobu ji zvládnete. Nejprve se podívejme na ilustrativní příklad popsaný krok za krokem. Poté může čtenář aplikovat to, co se naučil, na každé cvičení, které se objeví později.

Předpokládejme například, že musíte zohlednit následující výraz:
2xdva + 2xy - 3zx - 3zy
Tento algebraický výraz se skládá ze 4 monomiálů nebo termínů oddělených znaménky + a -, jmenovitě:
2xdva, 2xy, -3zx, -3zy
Podíváme-li se blíže, x je společné pro první tři, ale ne poslední, zatímco y je společné pro druhé a čtvrté a z je společné pro třetí a čtvrté..
V zásadě tedy neexistuje žádný společný faktor pro čtyři výrazy současně, ale pokud jsou seskupeny tak, jak bude uvedeno v následující části, je možné, že se objeví jeden, který pomůže napsat výraz jako produkt dvou nebo více faktorů.
Rejstřík článků
- 1 Příklady
- 2 Důležité otázky týkající se společného faktoru seskupením
- 3 cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Příklady
Faktorový výraz: 2xdva + 2xy - 3zx - 3zy
Krok 1: Skupina
2xdva + 2xy - 3zx - 3zy = (2xdva + 2xy) + (-3zx - 3zy)
Krok 2: Najděte společný faktor každé skupiny
2xdva + 2xy - 3zx - 3zy =
= (2xdva + 2xy) - (3zx + 3zy) =
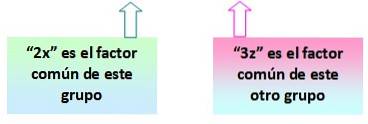
= 2x (x + y) - 3z (x + y)
JáDůležité: záporné znaménko je to také společný faktor, který je třeba vzít v úvahu.
Nyní si všimněte, že závorky (x + y) se opakují ve dvou pojmech získaných seskupením. To je společný činitel, o který se usiluje.
Krok 3: Rozdělte celý výraz
2xdva + 2xy - 3zx - 3zy = (x + y) (2x - 3z)
S předchozím výsledkem bylo dosaženo cíle factoringu, který není ničím jiným než transformací algebraického výrazu založeného na sčítání a odčítání termínů, do součinu dvou nebo více faktorů, v našem příkladu: (x + y) y (2x - 3z).
Důležité otázky týkající se společného faktoru seskupením
Vydání 1: Jak zjistit, že výsledek je správný?
Odpovědět: Distribuční vlastnost se použije na získaný výsledek a po zmenšení a zjednodušení se musí takto dosažený výraz shodovat s originálem, pokud ne, došlo k chybě.
V předchozím příkladu pracujeme obráceně s výsledkem, abychom zkontrolovali, zda je správný:
(x + y) (2x - 3z) = 2xdva -3zx + 2xy - 3zy
Vzhledem k tomu, že pořadí sčítání nemění součet, po použití distribuční vlastnosti jsou vráceny všechny původní výrazy, jsou zahrnuty znaky, proto je faktorizace správná.
Otázka 2: Mohlo to být seskupeno jiným způsobem?
Odpovědět: Existují algebraické výrazy, které umožňují více než jednu formu seskupování, a jiné, které to neumožňují. Ve vybraném příkladu si může čtenář vyzkoušet další možnosti samostatně, například seskupení takto:
2xdva + 2xy - 3zx - 3zy = (2xdva- 3zx) + (2xy - 3zy)
A můžete zkontrolovat, že výsledek je stejný, jako byl získán zde. Nalezení optimálního seskupení je otázkou praxe.
Otázka 3: Proč je nutné vzít z algebraického výrazu společný faktor?
Odpovědět: Protože existují aplikace, ve kterých faktorovaný výraz usnadňuje výpočty. Předpokládejme například, že chcete provést 2xdva + 2xy - 3zx - 3zy rovna 0. Jaké by byly možnosti?
Pro zodpovězení této otázky je faktorizovaná verze mnohem užitečnější než původní vývoj. Uvádí se takto:
(x + y) (2x - 3z) = 0
Jednou z možností, že výraz je 0, je, že x = -y, bez ohledu na hodnotu z. A druhá je, že x = (3/2) z, bez ohledu na hodnotu y.
Výcvik
- Cvičení 1
Vezměte společný faktor následujícího výrazu seskupením termínů:
sekera + ay + bx + podle
Řešení
První dva jsou seskupeny se společným faktorem „a“ a poslední dva se společným faktorem „b“:
ax + ay + bx + podle = a (x + y) + b (x + y)
Jakmile to provedete, odhalí se nový společný faktor, který je (x + y), takže:
ax + ay + bx + podle = a (x + y) + b (x + y) = (x + y) (a + b)
Další způsob seskupení
Tento výraz podporuje jiný způsob seskupování. Podívejme se, co se stane, pokud dojde k přeskupení termínů a vytvoření skupiny s těmi, které obsahují x, a další s těmi, které obsahují y:
ax + ay + bx + by = ax + bx + ay + by = x (a + b) + y (a + b)
Tímto způsobem je nový společný faktor (a + b):
ax + ay + bx + by = ax + bx + ay + by = x (a + b) + y (a + b) = (x + y) (a + b)
Což vede ke stejnému výsledku z první skupiny, která byla testována.
- Cvičení 2
Následující algebraický výraz je třeba psát jako součin dvou faktorů:
3. místo3 - 3. místodvab + 9abdva-nadva+ab-3bdva
Řešení
Tento výraz obsahuje 6 výrazů. Zkusme seskupit první a čtvrtý, druhý a třetí a nakonec pátý a šestý:
3. místo3 - 3. místodvab + 9abdva-nadva+ab-3bdva = (3a3 -nadva) + (- 3advab + 9abdva) + (ab-3b.)dva)
Nyní je započítána každá závorka:
= (3a3 -nadva) + (- 3advab + 9abdva) + (ab -3b.)dva) = adva (3a - 1) + 3ab (3b -a) + b (a-3b)
Na první pohled se zdá, že situace byla komplikovaná, ale čtenáře by to nemělo odradit, protože přepíšeme poslední výraz:
nadva (3a - 1) + 3ab (3b -a) + b (a-3b) = adva (3a - 1) + 3ab (3b-a) - b (3b-a)
Poslední dva termíny mají nyní společný faktor, který je (3b-a), takže je lze zohlednit. Je velmi důležité neztratit ze zřetele první termíndva (3a - 1), který musí vše doprovázet přidáváním, i když s ním nepracujete:
nadva (3a - 1) + 3ab (3b-a) - b (3b-a) = adva (3a - 1) + (3b-a) (3ab-b)
Výraz byl snížen na dva termíny a v posledním je objeven nový společný faktor, kterým je „b“. Nyní zůstává:
nadva (3a - 1) + (3b-a) (3ab-b) = adva (3a - 1) + b (3b-a) (3a-1)
Dalším společným faktorem, který se objeví, je 3a - 1:
nadva (3a - 1) + b (3b-a) (3a-1) = (3a - 1) [adva + b (3b-a)]
Nebo pokud dáváte přednost bez závorek:
(3a - 1) [adva + b (3b-a)] = (3a - 1) (adva -ab + 3bdva)
Může čtenář najít jiný způsob seskupování, který povede ke stejnému výsledku??

Reference
- Baldor, A. 1974. Elementární algebra. Kulturní Venezolana S.A.
- Jiménez, R. 2008. Algebra. Hala Prentice.
- Hlavní případy factoringu. Obnoveno z: julioprofe.net.
- UNAM. Základní matematika: Faktorizace seskupením termínů. Fakulta účetnictví a správy.
- Zill, D. 1984. Algebra a trigonometrie. MacGraw Hill.



Zatím žádné komentáře