
Typy transcendentních funkcí, definice, vlastnosti, příklady
The transcendentní funkce Základní jsou exponenciály, logaritmika, trigonometrické, inverzní trigonometrické funkce, hyperbolické a inverzní hyperbolické. To znamená, že jde o ty, které nelze vyjádřit pomocí polynomu, kvocientu polynomů nebo kořenů polynomů..
Neelementární transcendentní funkce jsou také známé jako speciální funkce a mezi nimi lze pojmenovat chybovou funkci. The algebraické funkce (polynomy, kvocienty polynomů a kořeny polynomů) společně s transcendentní funkce elementály tvoří to, co je v matematice známé jako základní funkce.
Transcendentní funkce jsou také považovány za ty, které jsou výsledkem operací mezi transcendentními funkcemi nebo mezi transcendentními a algebraickými funkcemi. Jedná se o operace: součet a rozdíl funkcí, součin a podíl funkcí, stejně jako složení dvou nebo více funkcí.
Rejstřík článků
- 1 Definice a vlastnosti
- 1.1 Exponenciální funkce
- 1.2 Vlastnosti exponenciální funkce
- 1.3 Logaritmická funkce
- 1.4 Vlastnosti logaritmické funkce
- 1.5 Sinusové, kosinusové a tangenciální funkce
- 2 Deriváty a integrály
- 2.1 Derivace exponenciální funkce
- 2.2 Integrál exponenciální funkce
- 2.3 Tabulka derivací a integrálů transcendentních funkcí
- 3 příklady
- 3.1 Příklad 1
- 3.2 Příklad 2
- 4 Odkazy
Definice a vlastnosti
Exponenciální funkce
Je to skutečná funkce skutečné nezávislé proměnné tvaru:
f (x) = a ^ x = aX
kde na je kladné reálné číslo (a> 0) pevně nazvaný základna. Háček nebo horní index se používají k označení potenciační operace.
Řekněme a = 2 pak funkce vypadá takto:
f (x) = 2 ^ x = 2X
Který bude vyhodnocen pro několik hodnot nezávislé proměnné x:

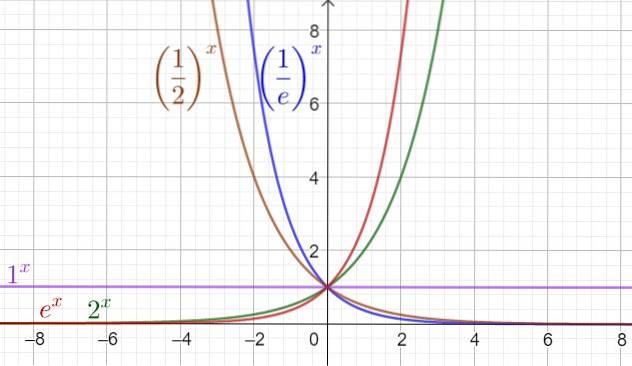
Níže je uveden graf, kde je exponenciální funkce reprezentována pro různé hodnoty základny, včetně základny a (Neperovo číslo a 72 2,72). Základna a je tak důležité, že obecně, když mluvíme o exponenciální funkci, myslíme na ni e ^ x, který je také označen exp (x).

Vlastnosti exponenciální funkce
Z obrázku 1 je vidět, že doménou exponenciálních funkcí jsou reálná čísla (Dom f = R) a rozsah nebo cesta jsou kladné reálné hodnoty (Ran f = R+).
Na druhou stranu bez ohledu na hodnotu základny a procházejí všechny exponenciální funkce bodem (0, 1) a bodem (1, a).
Když základna a> 1, pak se funkce zvyšuje a kdy 0 < a < 1 funkce klesá.
Křivky y = a ^ x a ze dne y = (1 / a) ^ x jsou symetrické kolem osy Y.
Až na případ a = 1, exponenciální funkce je injektivní, to znamená, že každé hodnotě obrazu odpovídá jedna a pouze jedna počáteční hodnota.
Logaritmická funkce
Jde o skutečnou funkci skutečné nezávislé proměnné založené na definici logaritmu čísla. Logaritmus základny na čísla X, Je to číslo Y pro získání argumentu je třeba zvýšit základnu X:
logna(x) = y ⇔ a ^ y = x
Toto je funkce logaritmu v základně na je inverzní funkce exponenciální funkce v bázi na.
Například:
logdva1 = 0, protože 2 ^ 0 = 1
Jiný případ, logdva4 = 2, protože 2 ^ 2 = 4
Logaritmus kořene 2 je logdva√2 = ½, protože 2 ^ ½ = √2
logdva ¼ = -2, protože 2 ^ (- 2) = ¼
Níže je uveden graf funkce logaritmu v různých základnách.
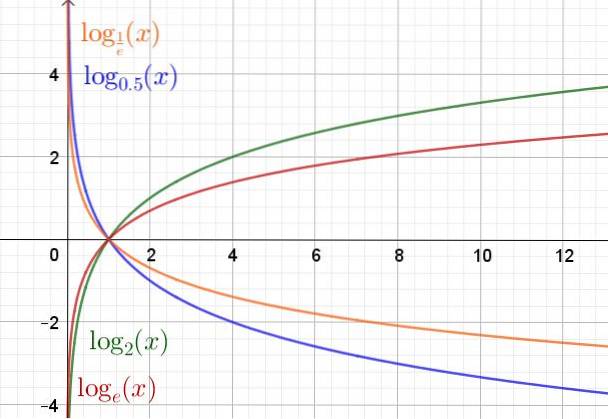
Vlastnosti logaritmické funkce
Doména funkce logaritmu y (x) = logna(X) jsou kladná reálná čísla R+. Rozsah nebo rozsah jsou reálná čísla R.
Bez ohledu na základnu prochází funkce logaritmu vždy bodem (1,0) a bod (a, 1) patří do grafu této funkce.
V případě, že základna a je větší než jednota (a> 1), funkce logaritmu se zvyšuje. Ale pokud (0 < a < 1) entonces es una función decreciente.
Sinusové, kosinusové a tangenciální funkce
Funkce sine přiřadí každé hodnotě x reálné číslo y, kde x představuje míru úhlu v radiánech. Pro získání hodnoty Sen (x) úhlu je úhel znázorněn v jednotkové kružnici a projekce uvedeného úhlu na svislou osu je sinus odpovídající tomuto úhlu.
Následující obrázek ukazuje (na obrázku 3) trigonometrickou kružnici a sinus pro různé úhlové hodnoty X1, X2, X3 a X4.
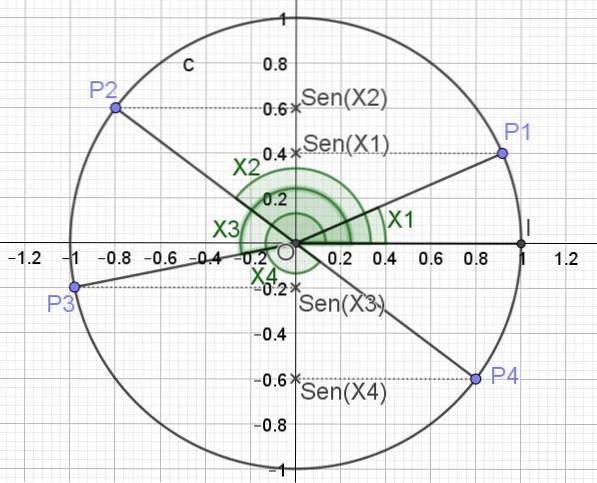
Takto definovaná maximální hodnota, kterou může mít funkce Sen (x), je 1, což nastane, když x = π / 2 + 2π n, kde n je celé číslo (0, ± 1, ± 2,). Minimální hodnota, kterou může funkce Sen (x) nabrat, nastane, když x = 3π / 2 + 2π n.
Kosinová funkce y = Cos (x) je definována podobným způsobem, ale projekce úhlových poloh P1, P2 atd. Se provádí na vodorovné ose trigonometrické kružnice..
Na druhou stranu, funkce y = Tan (x) je podíl mezi sinusovou funkcí a kosinusovou funkcí.
Níže je uveden graf transcendentních funkcí Sen (x), Cos (x) a Tan (x)
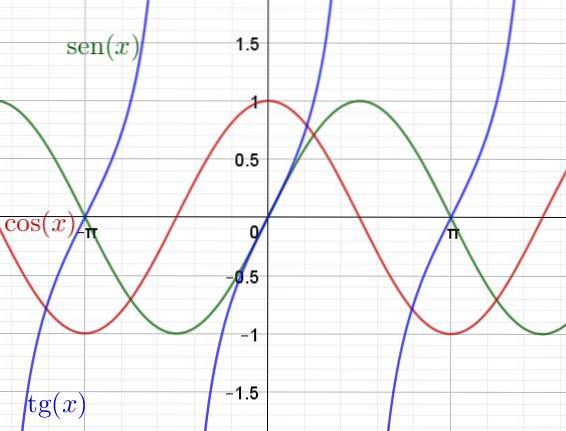
Deriváty a integrály
Derivace exponenciální funkce
Derivát Y ' exponenciální funkce y = a ^ x je funkce a ^ x vynásobeno přirozený logaritmus základny a:
y '= (a ^ x)' = a ^ x ln a
V konkrétním případě základny a, derivát exponenciální funkce je exponenciální funkce sama.
Integrál exponenciální funkce
Neurčitý integrál a ^ x je funkce sama o sobě dělená přirozeným logaritmem báze.
V konkrétním případě základny e je integrál exponenciální funkce samotná exponenciální funkce.
Tabulka derivací a integrálů transcendentních funkcí
Níže je uvedena souhrnná tabulka hlavních transcendentních funkcí, jejich derivátů a neurčitých integrálů (primitivní funkce):

Příklady
Příklad 1
Najděte funkci vyplývající ze složení funkce f (x) = x ^ 3 s funkcí g (x) = cos (x):
(f nebo g) (x) = f (g (x)) = cos3(X)
Jeho derivát a jeho neurčitý integrál jsou:
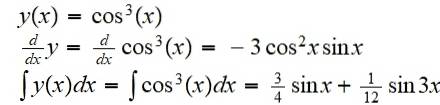
Příklad 2
Najděte složení funkce g s funkcí f, kde g a f jsou funkce definované v předchozím příkladu:
(g nebo f) (x) = g (f (x)) = cos (x3)
Je třeba poznamenat, že složení funkcí není komutativní operací.
Derivát a neurčitý integrál pro tuto funkci jsou:

Integrál byl ponechán označen, protože není možné přesně zapsat výsledek jako kombinaci elementárních funkcí.
Reference
- Počet jedné proměnné. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. listopadu 2008
- Věta o implicitní funkci: historie, teorie a aplikace. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9. listopadu. 2012
- Analýza více proměnných. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. prosince. 2010
- Systémová dynamika: modelování, simulace a řízení mechatronických systémů. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. března 2012
- Matematika a modelování. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. ledna 1999
- wikipedia. Transcendentní funkce. Obnoveno z: es.wikipedia.com



Zatím žádné komentáře