
Vlastnosti heptadekagonu, úhlopříčky, obvod, plocha

The heptadekagon je pravidelný mnohoúhelník se 17 stranami a 17 vrcholy. Jeho konstrukci lze provést v euklidovském stylu, tj. Pouze pomocí pravítka a kompasu. Byl to velký matematický génius Carl Friedrich Gauss (1777-1855), sotva 18 let, který našel postup pro jeho konstrukci v roce 1796.
Zdá se, že Gauss byl vždy velmi nakloněn tomuto geometrickému obrazci, a to do takové míry, že ode dne, kdy objevil jeho konstrukci, se rozhodl být matematikem. Říká se také, že chtěl, aby byl heptadekagon vyryt na jeho náhrobku.

Gauss také našel vzorec pro určení, které pravidelné polygony mají možnost konstruování pomocí pravítka a kompasu, protože některé nemají přesnou euklidovskou konstrukci.
Rejstřík článků
- 1 Charakteristiky heptadekagonu
- 2 Úhlopříčky a obvod
- 2.1 Obvod heptadekagonu
- 3 Oblast
- 3.1 Plocha vzhledem k straně
- 3.2 Plocha s daným poloměrem
- 4 příklady
- 4.1 Příklad 1
- 4.2 Příklad 2
- 5 Reference
Vlastnosti heptadekagonu
Pokud jde o jeho vlastnosti, jako každý polygon, je důležitý součet jeho vnitřních úhlů. V pravidelném mnohoúhelníku n stran je součet dán vztahem:
Sa (n) = (n -2) * 180 °.
U heptadekagonu počet stran n to je 17, což znamená, že součet jeho vnitřních úhlů je:
Sa (17) = (17 - 2) * 180 ° = 15 * 180 ° = 2700 °.
Tento součet, vyjádřený v radiánech, vypadá takto:
Sa (17) = (17 - 2) * π = 15 * π = 15π
Z výše uvedených vzorců lze snadno odvodit, že každý vnitřní úhel heptadekagonu má přesnou míru α danou:
α = 2700 ° / 17 = (15/17) π radiánů
Z toho vyplývá, že vnitřní úhel v přibližné formě je:
α ≈ 158 824 °
Úhlopříčky a obvod
Úhlopříčky a obvod jsou další důležité aspekty. V libovolném polygonu je počet úhlopříček:
D = n (n - 3) / 2 a v případě heptadekagonu, jako n = 17, to je pak to D = 119 úhlopříčky.
Na druhou stranu, pokud je známa délka každé strany heptadekagonu, pak se obvod běžného heptadekagonu zjistí jednoduše přidáním 17násobku této délky nebo ekvivalentu 17násobku délky d Na každé straně:
P = 17 d
Obvod heptadekagonu
Někdy je znám pouze poloměr r heptadekagonu, takže je nutné pro tento případ vytvořit vzorec.
Za tímto účelem je koncept apothem. Apothem je segment, který jde od středu pravidelného mnohoúhelníku do středu jedné strany. Apothem vzhledem k jedné straně je kolmý k této straně (viz obrázek 2).
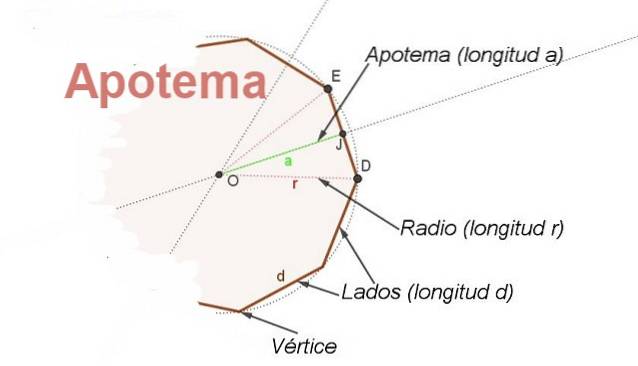
Kromě toho je apothem bisektorem úhlu se středním vrcholem a stranami na dvou po sobě jdoucích vrcholech mnohoúhelníku, což umožňuje najít vztah mezi poloměrem r a strana d.
Pokud se volá β do středového úhlu SRNA a s přihlédnutím k tomu, že apothem Úř. Věst je půlení, které máte EJ = d / 2 = r Sen (β / 2), odkud existuje vztah k nalezení délky d na straně známého mnohoúhelníku jeho poloměr r a jeho středový úhel β:
d = 2 r Sen (β / 2)
V případě heptadekagonu β = 360 ° / 17 takže máš:
d = 2 r Sen (180 ° / 17) ≈ 0,3675 r
Nakonec se získá vzorec pro obvod heptadekagonu, známý jeho poloměr:
P = 34 r Sen (180 ° / 17) ≈ 6,2475 r
Obvod heptadekagonu je blízký obvodu obvodu, který jej obklopuje, ale jeho hodnota je menší, to znamená, že obvod ohraničené kružnice je Pcir = 2π r ≈ 6,2832 r.
Plocha
Pro určení oblasti heptadekagonu budeme odkazovat na obrázek 2, který ukazuje strany a apothem pravidelného mnohoúhelníku n strany. Na tomto obrázku trojúhelník EOD má plochu rovnou základně d (strana mnohoúhelníku) krát výška na (polygon apothem) vydělte dva:
EOD plocha = (d x a) / 2
Tak známý apothem na heptadekagonu a boku d jeho oblast je:
Plocha heptadekagonu = (17/2) (d x a)
Plocha vzhledem k straně
Chcete-li získat vzorec pro plochu heptadekagonu, který zná délku jeho sedmnácti stran, je nutné získat vztah mezi délkou apothemu na a strana d.
S odkazem na obrázek 2 se získá následující trigonometrický vztah:
Tan (β / 2) = EJ / OJ = (d / 2) / a, bytost β do středového úhlu SRNA. Takže apothem na lze vypočítat, pokud je délka známa d ze strany mnohoúhelníku a středového úhlu β:
a = (d / 2) Cotan (β / 2)
Pokud je tento výraz nyní nahrazen apothemem, ve vzorci pro plochu heptadekagonu získaného v předchozí části máme:
Plocha heptadekagonu = (17/4) (ddva) Cotan (β / 2)
Bytost β = 360 ° / 17 pro heptadekagon, takže konečně máme požadovaný vzorec:
Plocha heptadekagonu = (17/4) (ddva) Cotan (180 ° / 17)
Plocha s daným poloměrem
V předchozích částech byl nalezen vztah mezi stranou d pravidelného mnohoúhelníku a jeho poloměrem r, přičemž tento vztah je následující:
d = 2 r Sen (β / 2)
Tento výraz pro d je představen ve výrazu získaném v předchozí části pro danou oblast. Pokud jsou provedeny příslušné substituce a zjednodušení, získá se vzorec, který umožňuje vypočítat plochu heptadekagonu:
Plocha heptadekagonu = (17/2) (rdva) Sen (β) = (17/2) (r.)dva) Sen (360 ° / 17)
Přibližný výraz pro oblast je:
Plocha heptadekagonu = 3,0706 (rdva)
Jak se dalo očekávat, tato oblast je o něco menší než oblast kruhu, který ohraničuje heptadekagon. NAcir = π rdva ≈ 3,1416 rdva. Přesněji řečeno, je to o 2% méně než u jeho popsané kružnice.
Příklady
Příklad 1
Jakou hodnotu musí mít poloměr a průměr ohraničeného obvodu, aby měl heptadekagon strany 2 cm? Najděte také hodnotu obvodu.
K zodpovězení otázky je nutné si pamatovat vztah mezi stranou a poloměrem pravidelného n-stranného mnohoúhelníku:
d = 2 r Sen (180 ° / n)
Pro heptadekagon n = 17, aby d = 0,3675 r, to znamená, že poloměr heptadekagonu je r = 2 cm / 0,3675 = 5,4423 cm nebo
Průměr 10,8844 cm.
Obvod 2 cm bočního heptadekagonu je P = 17 * 2 cm = 34 cm.
Příklad 2
Jaká je plocha běžného heptadekagonu se stranou 2 cm?
Musíme se odvolat na vzorec zobrazený v předchozí části, který nám umožňuje najít oblast heptadekagonu, pokud má délku d na tvé straně:
Plocha heptadekagonu = (17/4) (ddva) / Tan (180 ° / 17)
Při střídání d = 2 cm ve výše uvedeném vzorci získáte:
Plocha = 90,94 cm
Reference
- C. E. A. (2003). Prvky geometrie: s cvičeními a geometrií kompasu. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematika 2. Grupo Redakční Patria.
- Freed, K. (2007). Objevte mnohoúhelníky. Benchmark Education Company.
- Hendrik, V. (2013). Zobecněné polygony. Birkhäuser.
- IGER. (s.f.). Matematika v prvním semestru Tacaná. IGER.
- Jr. geometrie. (2014). Mnohoúhelníky. Lulu Press, Inc..
- Miller, Heeren a Hornsby. (2006). Mathematics: Reasoning And Applications (desáté vydání). Pearson Education.
- Patiño, M. (2006). Matematika 5. Redakční program.
- Sada, M. 17stranný pravidelný mnohoúhelník s pravítkem a kompasem. Obnoveno z: geogebra.org
- Wikipedia. Heptadekagon. Obnoveno z: es.wikipedia.com



Zatím žádné komentáře