The Coulombův zákon je to fyzikální zákon, který řídí interakci mezi elektricky nabitými objekty. Vyslovil to francouzský vědec Charles Augustin de Coulomb (1736-1806), a to díky výsledkům jeho experimentů využívajících torzní rovnováhu.
V roce 1785 Coulomb bezpočetně experimentoval s malými elektricky nabitými koulemi, například pohybem dvou koulí blíže nebo dále od sebe, přičemž se měnila velikost jejich náboje a také jejich znamení. Každou odpověď vždy pečlivě sledujte a zaznamenávejte.
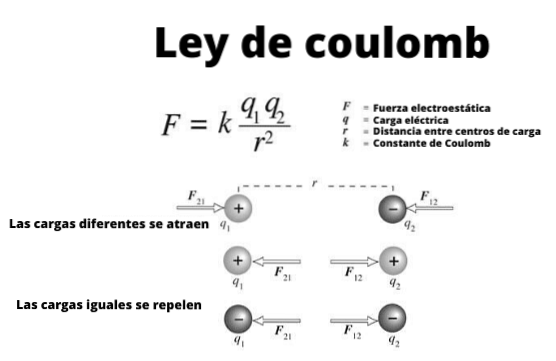
Tyto malé koule lze považovat za bodová zatížení, tj. objekty, jejichž rozměry jsou nevýznamné. A splňují, jak je známo již od dob starověkých Řeků, že poplatky stejného znamení odpuzují a poplatky jiného znamení přitahují..
S ohledem na tuto skutečnost Charles Coulomb zjistil následující:
-Přitažlivá nebo odpudivá síla mezi dvěma bodovými náboji je přímo úměrná součinu velikosti nábojů.
-Tato síla je vždy směrována podél linie, která spojuje nálože.
-Nakonec je velikost síly nepřímo úměrná druhé mocnině vzdálenosti mezi náboji.
Rejstřík článků
Díky těmto pozorováním dospěl Coulomb k závěru, že velikost síly F mezi dvěma bodovými náboji co1 Y codva, oddělil vzdálenost r, je matematicky uveden jako:
Protože síla je vektorová velikost, je zcela definován jednotkový vektor r ve směru přímky spojující náboje (jednotkový vektor má velikost rovnou 1).
Konstanta proporcionality nezbytná k transformaci předchozího výrazu na rovnost se dále nazývá ka nebo jednoduše k: the elektrostatická konstanta nebo Coulombova konstanta.
A konečně, Coulombův zákon je stanoven pro bodové poplatky, dané:
Síla, jako vždy v mezinárodním systému jednotek, přichází v newtonu (N). Co se týče poplatků, jednotka je pojmenována coulomb (C) na počest Charlese Coulomba a nakonec vzdálenost r přichází v metrech (m).
Při bližším pohledu na výše uvedenou rovnici je jasné, že elektrostatická konstanta musí mít jednotky N.mdva / C.dva, výsledkem je získání newtonů. Hodnota konstanty byla stanovena experimentálně jako:
ka = 8,89 x 10 9 N.mdva / C.dva ≈ 9 x 10 9 N.mdva / C.dva
Obrázek 1 ilustruje interakci mezi dvěma elektrickými náboji: pokud mají stejné znaménko, odpuzují je, jinak přitahují.
Všimněte si, že Coulombův zákon je v souladu s třetím Newtonovým zákonem nebo zákonem akce a reakce, proto velikosti F1 Y Fdva jsou stejné, směr je stejný, ale smysly jsou opačné.
Při řešení problémů interakcí mezi elektrickými náboji je třeba vzít v úvahu následující:
- Rovnice platí výlučně v případě bodových nábojů, tj. Elektricky nabitých objektů, ale velmi malých rozměrů. Pokud mají načtené objekty měřitelné rozměry, je nutné je rozdělit na velmi malá zatížení a poté přidat příspěvky každého z těchto zatížení, pro které je vyžadován integrální výpočet..
- Elektrická síla je vektorová veličina. Pokud existují více než dva interagující náboje, čistá síla na náboj qi je dán principem superpozice:
Fsíť = Fi1 + Fi2 + Fi3 + Fi4 +… = ∑ Fij
Kde dolní index j se rovná 1, 2, 3, 4 ... a představuje každý ze zbývajících poplatků.
- Měli byste být vždy v souladu s jednotkami. Nejčastěji se pracuje s elektrostatickou konstantou v jednotkách SI, pak je nutné zajistit, aby náboje byly v coulombech a vzdálenosti v metrech.
- Nakonec platí rovnice, když jsou náboje ve statické rovnováze.
Na následujícím obrázku jsou dva bodové náboje + q a + 2q. Třetí bodový náboj -q je umístěn na P. Je požádán, aby našel elektrickou sílu na tomto náboji kvůli přítomnosti ostatních.
První věcí je vytvořit vhodný referenční systém, kterým je v tomto případě vodorovná osa nebo osa x. Původ takového systému může být kdekoli, ale pro větší pohodlí bude umístěn na P, jak ukazuje obrázek 4a:
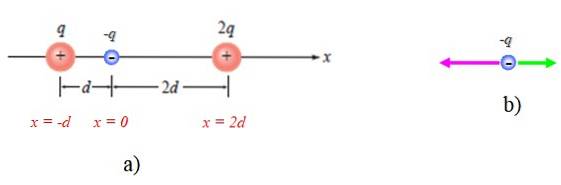
Je také zobrazen diagram sil na -q s přihlédnutím k tomu, že je přitahován dalšími dvěma (obrázek 4b).
Zavolejme F1 síla vyvíjená nábojem q na náboj -q, je směrována podél osy x a směřuje v záporném směru, proto:
Analogicky se to počítá Fdva:
Všimněte si, že velikost Fdva je polovina z toho F1, i když je zatížení dvojnásobné. Abychom našli čistou sílu, nakonec se přidají vektorově F1 Y Fdva:
Fsíť = (-k + k / 2). (qdva / ddva) (X) N = - (k / 2). (Qdva / ddva) (X) N
Dvě polystyrenové koule stejné hmotnosti m = 9,0 x 10-8 kg mají stejný kladný náboj Q a jsou zavěšeny hedvábnou nití o délce L = 0,98 m. Koule jsou odděleny vzdáleností d = 2 cm. Vypočítejte hodnotu Q.
Situace prohlášení je popsána na obrázku 5a.
Vybereme jednu z koulí a nakreslíme na ní diagram izolovaného tělesa, který obsahuje tři síly: váhu Ž, napětí v laně T a elektrostatické odpuzování F, jak je znázorněno na obrázku 5b. A teď kroky:
Hodnota θ / 2 se vypočítá pomocí trojúhelníku na obrázku 5c:
θ / 2 = arcsen (1 x 10-dva/ 0,98) = 0,585 °
Dále musíme použít druhý Newtonův zákon a nastavit jej na 0, protože náboje jsou ve statické rovnováze. Důležité je napětí T je šikmý a má dvě složky:
∑FX = -T.sin θ + F = 0
∑FY = T.cos θ - W = 0
Vyřešíme velikost napětí z poslední rovnice:
T = W / cos θ = mg / cos θ
Tato hodnota je dosazena do první rovnice, aby se zjistila velikost F:
F = T sin θ = mg (sin θ / cos θ) = mg. tg θ
Protože F = k Qdva / ddva, vymaže Q:
Q = 2 × 10-jedenáct C.
Kontrola Coulombova zákona je snadná pomocí torzní váhy podobné té, kterou použil Coulomb ve své laboratoři..
Existují dvě malé kuličky bezinky, z nichž jedna je uprostřed váhy a je zavěšena na niti. Experiment spočívá v dotyku vybitých bezových koulí s další kovovou koulí nabitou nábojem Q..
Náboj je okamžitě rozdělen rovnoměrně mezi dvě koule černého bezu, ale poté, co se jedná o náboje stejného znamení, se navzájem odpuzují. Na zavěšenou kouli působí síla, která způsobí zkroucení niti, ze kterého visí, a okamžitě se vzdaluje od pevné koule.
Pak vidíme, že několikrát osciluje, dokud nedosáhne rovnováhy. Pak je torze tyče nebo nitě, která je drží, vyvážena elektrostatickou odpudivou silou.
Pokud byly původně koule na 0 °, nyní pohybující se koule otočila o úhel θ. Kolem stupnice je páska odstupňovaná ve stupních k měření tohoto úhlu. Dříve stanovením torzní konstanty lze snadno vypočítat odpudivou sílu a hodnotu náboje získaného bezolovými koulemi.
Zatím žádné komentáře