The Faradayův zákon v elektromagnetismu říká, že měnící se tok magnetického pole je schopen indukovat elektrický proud v uzavřeném obvodu.
V roce 1831 experimentoval anglický fyzik Michael Faraday s pohybujícími se vodiči v magnetickém poli a také s měnícími se magnetickými poli, která procházela pevnými vodiči..
Faraday si uvědomil, že pokud v průběhu času mění tok magnetického pole, dokáže vytvořit napětí úměrné této změně. Pokud ε je napětí nebo indukovaná elektromotorická síla (indukovaná emf) a Φ je tok magnetického pole, v matematické formě to lze vyjádřit:
| ε | = ΔΦ / Δt
Kde symbol Δ označuje změnu množství a sloupce v emf udávají absolutní hodnotu. Jelikož se jedná o uzavřený obvod, může proud proudit jedním nebo druhým směrem.
Magnetický tok produkovaný magnetickým polem přes povrch se může lišit mnoha způsoby, například:
-Pohyb tyčového magnetu kruhovou smyčkou.
-Zvýšení nebo snížení intenzity magnetického pole, které prochází smyčkou.
-Ponechání pole pevné, ale pomocí nějakého mechanismu změnit oblast smyčky.
-Kombinace výše uvedených metod.
Rejstřík článků
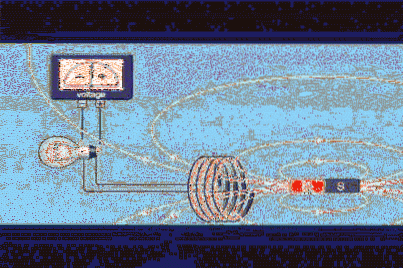
Předpokládejme, že máte uzavřený obvod oblasti A, jako je kruhová smyčka nebo vinutí stejné jako na obrázku 1, a že máte magnet, který vytváří magnetické pole B.
Tok magnetického pole Φ je skalární veličina, která se vztahuje k počtu siločar, které procházejí oblastí A. Na obrázku 1 jsou bílé čáry, které opouštějí severní pól magnetu a vracejí se přes jižní.
Intenzita pole bude úměrná počtu řádků na jednotku plochy, takže vidíme, že na pólech je velmi intenzivní. Ale můžeme mít velmi intenzivní pole, které neprodukuje tok ve smyčce, čehož můžeme dosáhnout změnou orientace tohoto (nebo magnetu).
Pro zohlednění faktoru orientace je tok magnetického pole definován jako skalární součin mezi B Y n, bytost n jednotkový normální vektor k povrchu smyčky, který označuje jeho orientaci:
Φ = B•n A = BA.cosθ
Kde θ je úhel mezi B Y n. Pokud například B Y n jsou kolmé, tok magnetického pole je nulový, protože v takovém případě je pole tečné k rovině smyčky a nemůže projít jejím povrchem.
Místo toho ano B Y n jsou rovnoběžné, znamená to, že pole je kolmé na rovinu smyčky a čáry jím procházejí, pokud je to možné.
Jednotkou v mezinárodním systému pro F je weber (W), kde 1 W = 1 T.mdva (čtěte „tesla na metr čtvereční“).
Na obrázku 1 vidíme, že polarita napětí se mění s pohybem magnetu. Polarita je stanovena Lenzovým zákonem, který říká, že indukované napětí musí být proti variaci, která jej vytváří.
Pokud se například magnetický tok produkovaný magnetem zvýší, vytvoří se ve vodiči, který cirkuluje, proud, který vytváří vlastní tok, který je proti tomuto nárůstu..
Pokud naopak tok vytvářený magnetem klesá, indukovaný proud cirkuluje takovým způsobem, že jeho vlastní tok působí proti uvedenému poklesu..
Abychom tento jev zohlednili, před Faradayův zákon se umístí záporné znaménko a již není nutné umisťovat pruhy absolutní hodnoty:
ε = -ΔΦ / Δt
Toto je zákon Faraday-Lenz. Pokud je variace toku nekonečně malá, jsou delty nahrazeny diferenciály:
ε = -dΦ / dt
Výše uvedená rovnice platí pro smyčku. Ale pokud máme cívku N závitů, výsledek je mnohem lepší, protože emf se znásobí N krát:
ε = - N (dΦ / dt)
Aby proud zapnul produkovanou žárovku, musí existovat relativní pohyb mezi magnetem a smyčkou. Toto je jeden ze způsobů, jak se tok může měnit, protože tímto způsobem se mění intenzita pole procházejícího smyčkou..
Jakmile pohyb magnetu ustane, žárovka zhasne, i když je magnet ponechán stále uprostřed smyčky. K cirkulaci proudu, který zapíná žárovku, je potřeba to, že tok pole se mění.
Když se magnetické pole mění s časem, můžeme to vyjádřit jako:
B = B (t).
Udržováním konstantní oblasti A smyčky a jejím fixováním v konstantním úhlu, který je v případě obrázku 0 °, pak:
Pokud je možné změnit oblast smyčky, ponechat její orientaci pevnou a umístit ji do středu konstantního pole, indukovaný emf je dán vztahem:
Jedním ze způsobů, jak toho dosáhnout, je umístit tyč, která klouže po vodivé kolejnici určitou rychlostí, jak je znázorněno na následujícím obrázku.
Tyč a kolejnice, plus žárovka nebo odpor spojený s vodivými dráty, tvoří uzavřený obvod ve tvaru obdélníkové smyčky..
Při posouvání lišty, délka X zvětšuje nebo zmenšuje, a tím se mění plocha smyčky, což je dostatečné pro vytvoření proměnného toku.
Jak jsme již řekli, pokud je úhel mezi B a normála smyčky se mění, tok pole se mění podle:
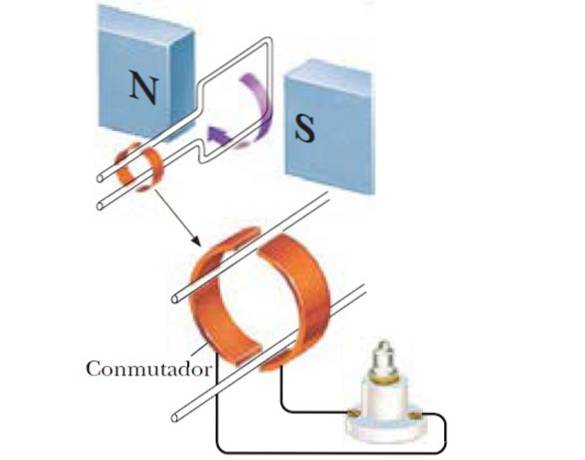
Získá se tak sinusový generátor, a pokud se místo jediné cívky použije více N cívek, indukovaný emf je větší:
Kruhová cívka N závitů a poloměru R se otáčí s úhlovou frekvencí ω uprostřed magnetického pole o velikosti B. Najděte výraz pro maximální emf indukovaný v cívce.
Výraz pro emf vyvolaný rotací se použije, když má cívka N závitů, s vědomím, že:
-Plocha cívky je A = πRdva
-Úhel θ se mění v závislosti na čase jako θ = ωt
Je důležité si uvědomit, že první θ = ωt je nahrazeno Faradayovým zákonem a již brzy je odvozeno s ohledem na čas:
ε = -NBA (cos θ) '= -NB (πRdva). [cos (ωt)] '= NBω (πRdva) sin (ωt)
Jelikož je požadováno maximální emf, dochází k němu vždy, když sin ωt = 1, takže nakonec:
εmax = NBω (πRdva)
Zatím žádné komentáře