The zákon z Hardy-Weinberg, Také se nazývá Hardy-Weinbergův princip nebo rovnováha, sestává z matematické věty, která popisuje hypotetickou diploidní populaci se sexuální reprodukcí, která se nevyvíjí - frekvence alel se nemění z generace na generaci.
Tento princip předpokládá pět podmínek nezbytných k tomu, aby populace zůstala konstantní: absence toku genů, absence mutací, náhodné páření, absence přirozeného výběru a nekonečně velká velikost populace. Tímto způsobem, při absenci těchto sil, populace zůstane v rovnováze.
Pokud některý z výše uvedených předpokladů není splněn, dojde ke změně. Z tohoto důvodu jsou přirozený výběr, mutace, migrace a genetický drift čtyři evoluční mechanismy..
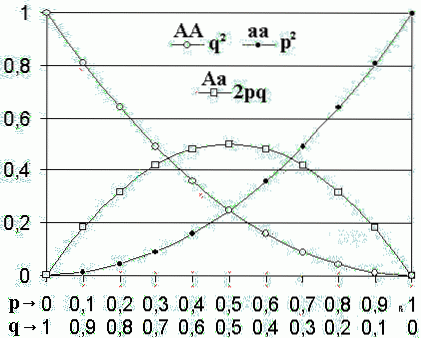
Podle tohoto modelu, když jsou alelové frekvence populace p Y co, frekvence genotypu budou pdva, dvapq Y codva.
Hardyho-Weinbergovu rovnováhu můžeme použít při výpočtu frekvencí určitých sledovaných alel, například k odhadu podílu heterozygotů v lidské populaci. Můžeme také ověřit, zda je populace v rovnováze nebo ne, a navrhnout hypotézy, že síly na tuto populaci působí..
Rejstřík článků
Hardy-Weinbergův princip se narodil v roce 1908 a za své jméno vděčí svým vědcům G.H. Hardy a W. Weinberg, kteří nezávisle dospěli ke stejným závěrům.
Před tím se problémem v roce 1902 zabýval další biolog jménem Udny Yule. Yule začala se sadou genů, ve kterých byly frekvence obou alel 0,5 a 0,5. Biolog ukázal, že frekvence byly udržovány během následujících generací.
Přestože Yule dospěl k závěru, že frekvence alel lze udržet stabilní, jeho interpretace byla příliš doslovná. Věřil, že jediný stav rovnováhy byl nalezen, když frekvence odpovídaly hodnotě 0,5.
Yule vášnivě diskutovala o svých nových poznatcích s R.C. Punnett - široce známý v oblasti genetiky pro vynález slavného „Punnettova náměstí“. Ačkoli Punnett věděl, že se Yule mýlí, nenašel matematický způsob, jak to dokázat..
Punnett proto kontaktoval svého matematického přítele Hardyho, kterému se to podařilo okamžitě vyřešit, opakováním výpočtů s použitím obecných proměnných, a nikoli pevné hodnoty 0,5, jak to udělal Yule..
Populační genetika si klade za cíl studovat síly, které vedou ke změnám alelických frekvencí v populacích, integrovat evoluční teorii Charlese Darwina přirozeným výběrem a mendelovskou genetikou. Dnes jeho principy poskytují teoretický základ pro pochopení mnoha aspektů evoluční biologie..
Jednou z klíčových myšlenek populační genetiky je vztah mezi změnami relativního množství znaků a změnami relativního množství alel, které jej regulují, vysvětleno Hardy-Weinbergovým principem. Tato věta ve skutečnosti poskytuje koncepční rámec pro populační genetiku..
Ve světle populační genetiky je koncept evoluce následující: změna frekvencí alel v průběhu generací. Když nedojde ke změně, nedojde k žádné evoluci.
Hardy-Weinbergova rovnováha je nulový model, který nám umožňuje specifikovat chování genových a alelických frekvencí napříč generacemi. Jinými slovy, je to model, který popisuje chování genů v populacích za řady konkrétních podmínek..
V Hardy-Weinbergmově větě je alelická frekvence NA (dominantní alela) je reprezentována písmenem p, zatímco alelická frekvence na (recesivní alela) je reprezentována písmenem co.
Očekávané frekvence genotypu jsou pdva, dvapq Y codva, pro homozygotní dominantní (AA), heterozygotní (Aa) a homozygotní recesivní (aa), v uvedeném pořadí.
Pokud jsou na tomto místě pouze dvě alely, musí se součet frekvencí těchto dvou alel nutně rovnat 1 (p + q = 1). Binomická expanze (p + q)dva představují frekvence genotypu pdva + dvapq + qdva = 1.
V populaci se jednotlivci, kteří ji skládají, křížili, aby dali vzniknout potomkům. Obecně můžeme poukázat na nejdůležitější aspekty tohoto reprodukčního cyklu: produkci gamet, jejich fúzi za vzniku zygoty a vývoj embrya za vzniku nové generace..
Představte si, že můžeme ve zmíněných událostech vystopovat Mendelianův genový proces. Děláme to proto, že chceme vědět, zda a proč alela nebo genotyp zvýší nebo sníží frekvenci..
Abychom pochopili, jak se frekvence genů a alel liší v populaci, budeme sledovat produkci gamet sady myší. V našem hypotetickém příkladu dochází k páření náhodně, kde jsou všechny spermie a vajíčka náhodně smíchány..
V případě myší tento předpoklad není pravdivý a jedná se pouze o zjednodušení pro usnadnění výpočtů. U některých skupin zvířat, jako jsou některé ostnokožce a jiné vodní organismy, jsou však gamety vyloučeny a náhodně se srazí..
Nyní zaměřme naši pozornost na konkrétní místo se dvěma alelami: NA Y na. Podle zákona vyhlášeného Gregorem Mendelem dostává každá gameta alelu z lokusu A. Předpokládejme, že 60% vajíček a spermií dostane alelu NA, zatímco zbývajících 40% dostalo alelu na.
Proto je frekvence alely NA je 0,6 a alela na je 0,4. Tato skupina gamet bude náhodně nalezena k vzniku zygoty. Jaká je pravděpodobnost, že vytvoří každý ze tří možných genotypů? K tomu musíme znásobit pravděpodobnosti následujícím způsobem:
Genotyp AA: 0,6 x 0,6 = 0,36.
Genotyp Aa: 0,6 x 0,4 = 0,24. V případě heterozygotu existují dvě formy, ve kterých může vzniknout. První, že spermie nese alelu NA a vajíčko alela na, nebo obrácený případ, sperma na a vajíčko NA. Proto přidáme 0,24 + 0,24 = 0,48.
Genotyp aa: 0,4 x 0,4 = 0,16.
Nyní si představme, že se tyto zygoty vyvinou a stanou se dospělými myšmi, které budou opět produkovat gamety, očekávali bychom, že frekvence alel budou stejné nebo odlišné od předchozí generace?
Genotyp AA bude produkovat 36% gamet, zatímco heterozygoti budou produkovat 48% gamet a genotyp aa 16%.
Pro výpočet nové alelové frekvence přidáme frekvenci homozygotů plus polovinu heterozygotů, a to následovně:
Frekvence alely NA: 0,36 + ½ (0,48) = 0,6.
Frekvence alely na: 0,16 + ½ (0,48) = 0,4.
Pokud je porovnáme s počátečními frekvencemi, uvědomíme si, že jsou identické. Proto podle koncepce evoluce, protože nedochází ke změnám ve frekvencích alel po generace, je populace v rovnováze - nevyvíjí se..
Jaké podmínky musí předchozí populace splňovat, aby její frekvence alel zůstaly po generace konstantní? V modelu Hardy-Weinbergovy rovnováhy splňuje populace, která se nevyvíjí, následující předpoklady:
Populace musí mít extrémně velkou velikost, aby se zabránilo stochastickým nebo náhodným účinkům driftu genů.
Když jsou populace malé, účinek driftu genu (náhodné změny ve frekvencích alel, z jedné generace na druhou) v důsledku chyby vzorkování je mnohem větší a může vést k fixaci nebo ztrátě určitých alel..
Migrace v populaci neexistují, takže alely, které mohou změnit genové frekvence, nemohou přijít ani odejít.
Mutace jsou změny v sekvenci DNA a mohou mít různé příčiny. Tyto náhodné změny modifikují genofond v populaci zavedením nebo eliminací genů v chromozomech.
Míchání gamet musí být provedeno náhodně - jako předpoklad, který jsme použili v příkladu myši. Proto by mezi jednotlivci v populaci neměl existovat výběr partnera, včetně příbuzenské plemenitby (reprodukce příbuzných jedinců).
Pokud páření není náhodné, nezpůsobí to změnu frekvencí alel z jedné generace na druhou, ale může generovat odchylky od očekávaných frekvencí genotypu..
Neexistuje žádný rozdílný reprodukční úspěch jedinců s různými genotypy, které by mohly změnit alelové frekvence v populaci..
Jinými slovy, v hypotetické populaci mají všechny genotypy stejnou pravděpodobnost reprodukce a přežití..
Pokud populace nesplňuje těchto pět podmínek, výsledkem je vývoj. Logicky přirozené populace tyto předpoklady nesplňují. Proto se Hardy-Weinbergův model používá jako nulová hypotéza, která nám umožňuje provést přibližné odhady genových a alelických frekvencí..
Kromě nedostatku těchto pěti podmínek existují další možné příčiny, proč populace není v rovnováze.
Jeden z nich nastane, když loci jsou spojeny s pohlavím nebo jevy zkreslení v segregaci nebo meiotický pohon (když se každá kopie genu nebo chromozomu nepřenáší se stejnou pravděpodobností do další generace).
Ve Spojených státech má přibližně jeden z 10 000 novorozenců stav nazývaný fenylketonurie..
Tato porucha je vyjádřena pouze u recesivních homozygotů u metabolické poruchy. Na základě těchto údajů, jaká je frekvence nositelů nemoci v populaci??
Abychom mohli použít Hardyho-Weinbergovu rovnici, musíme předpokládat, že volba partnera nesouvisí s genem souvisejícím s patologií a neexistuje žádná příbuzenská plemenitba..
Dále předpokládáme, že ve Spojených státech neexistují žádné migrační jevy, neexistují žádné nové mutace fenylketonurie a pravděpodobnost reprodukce a přežití je mezi genotypy stejná..
Pokud jsou podmínky uvedené výše pravdivé, můžeme použít Hardy-Weinbergovu rovnici k provedení výpočtů souvisejících s daným problémem..
Víme, že existuje jeden případ onemocnění každých 10 000 porodů, takže codva = 0,0001 a frekvence recesivní alely bude druhou odmocninou této hodnoty: 0,01.
Co p = 1 - co, musíme p je 0,99. Nyní máme frekvenci obou alel: 0,01 a 0,99. Nosná frekvence označuje frekvenci heterozygotů, která se počítá jako 2pq. Tedy 2pq = 2 x 0,99 x 0,01 = 0,0198.
To odpovídá přibližně 2% populace. Pamatujte, že toto je pouze přibližný výsledek.
Pokud známe počet jednotlivých genotypů v populaci, můžeme usoudit, zda je v Hardy-Weinbergově rovnováze. Kroky k vyřešení těchto typů problémů jsou následující:
p = D + ½ H
q = R + ½ H
Například chceme ověřit, zda je následující populace motýlů v Hardy-Weinbergově rovnováze: existuje 79 jedinců homozygotního dominantního genotypu (AA), 138 heterozygota (Aa) a 61 homozygotních recesivních (aa).
Prvním krokem je výpočet pozorovaných frekvencí. Děláme to vydělením počtu jedinců na genotyp celkovým počtem jedinců:
D = 79/278 = 0,28
H = 138/278 = 0,50
R = 61/278 = 0,22
Prvním krokem k ověření, zda jsem udělal dobře, je přidání všech frekvencí a mělo by dát 1.
Druhým krokem je výpočet frekvencí alel.
p = 0,28 + ½ (0,50) = 0,53
co = 0,22 + ½ (0,50) = 0,47
S těmito údaji mohu vypočítat očekávané frekvence genotypu (pdva, dvaproč a codva)
pdva = 0,28
dvapq = 0,50
codva = 0,22
Počítám očekávaná čísla a vynásobím očekávané frekvence počtem jednotlivců. V tomto případě je počet pozorovaných a očekávaných jedinců stejný, takže mohu dojít k závěru, že populace je v rovnováze.
Pokud získaná čísla nejsou totožná, musím provést zmíněný statistický test (Xdva od Pearsona).
Zatím žádné komentáře