
Ohmovy zákonné jednotky a vzorec, výpočet, příklady, cvičení
The Ohmův zákon, ve své makroskopické formě znamená, že napětí a intenzita proudu v obvodu jsou přímo úměrné, odpor je konstanta úměrnosti. Označením těchto tří veličin jako V, I a R, Ohmův zákon říká, že: V = I.R..
Podobně je Ohmův zákon zobecněn tak, aby zahrnoval prvky obvodu, které nejsou čistě odporové v obvodech střídavého proudu, tímto způsobem má následující podobu: V = I.Z.

Kde Z je impedance, která také představuje opozici vůči průchodu střídavého proudu prvkem obvodu, například kondenzátorem nebo indukčností.
Je třeba poznamenat, že ne všechny materiály a prvky obvodů splňují Ohmův zákon. Ty, ve kterých je platný, se nazývají prvky ohmický, a ve kterém není splněna, jsou neohmický nebo nelineární.
Běžné elektrické rezistory jsou ohmického typu, ale diody a tranzistory nejsou, protože vztah mezi napětím a proudem v nich není lineární..
Ohmův zákon vděčí za své jméno německému fyzikovi a matematikovi narozenému v Bavorsku Georgovi Simonovi Ohmovi (1789-1854), který svou kariéru strávil studiem chování elektrických obvodů. Jednotka elektrického odporu v mezinárodním systému SI byla pojmenována na jeho počest: ohm, což je také vyjádřeno řeckým písmenem Ω.
Rejstřík článků
- 1 Jak se počítá?
- 1.1 Odpor vodiče
- 2 Příklady
- 2.1 Pokus o kontrolu Ohmova zákona
- 2.2 Hydraulická analogie Ohmova zákona
- 3 cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Jak se to počítá?
Ačkoli je nejznámější makroskopická forma Ohmova zákona, protože spojuje veličiny, které jsou v laboratoři snadno měřitelné, mikroskopický tvar souvisí dvě důležité vektorové veličiny: elektrické pole A a hustota proudu J:
J = σ.A
Kde σ je elektrická vodivost materiálu, vlastnost, která udává, jak snadné je vést proud. Pro jeho část J je vektor, jehož velikost je kvocient mezi aktuální intenzitou I a plochou průřezu A, kterou cirkuluje.
Je logické předpokládat, že existuje přirozené spojení mezi elektrickým polem uvnitř materiálu a elektrickým proudem, který ním cirkuluje, takže čím větší je proud, tím více proudu.
Proud ale není vektor, protože nemá směr v prostoru. Místo toho vektor J je kolmá - nebo kolmá - k ploše průřezu vodiče a jeho směr je směr proudu.
Z této formy Ohmova zákona se dostáváme k první rovnici za předpokladu vodiče délky ℓ a průřezu A a dosazením velikostí J Y A pro:
J = I / A
E = V / ℓ
J = σ.E → I / A = σ. (V / ℓ)
V = (ℓ / σ.A). I.
Inverzní vodivost se nazývá odpor a je označeno řeckým písmenem ρ:
1 / σ = ρ
Proto:
V = (ρℓ / A) .I = R.I
Odpor vodiče
V rovnici V = (ρℓ / A). I., konstanta (ρℓ / A) je odpor, proto:
R = ρℓ / A
Odpor vodiče závisí na třech faktorech:
-Jeho měrný odpor ρ, typický pro materiál, ze kterého je vyroben.
-Délka ℓ.
-Oblast A jejího průřezu.
Čím vyšší je ℓ, tím větší je odpor, protože nosiče proudu mají více příležitostí ke srážce s jinými částicemi uvnitř vodiče a ztrátě energie. A naopak, čím vyšší A, tím snazší je pro současné nosiče uspořádaný pohyb materiálem..
Konečně v molekulární struktuře každého materiálu spočívá snadnost, s jakou látka umožňuje průchod elektrického proudu. Například kovy, jako je měď, zlato, stříbro a platina, s nízkým měrným odporem, jsou dobrými vodiči, zatímco dřevo, guma a olej nejsou, což je důvod, proč mají vyšší měrný odpor..
Příklady
Zde jsou dva ilustrativní příklady Ohmova zákona.
Pokuste se zkontrolovat Ohmův zákon
Jednoduchý zážitek ilustruje Ohmův zákon, k tomu potřebujete kousek vodivého materiálu, zdroj proměnného napětí a multimetr.
Mezi konci vodivého materiálu je vytvořeno napětí V, které se musí postupně měnit. S proměnným zdrojem energie lze nastavit hodnoty uvedeného napětí, které se měří multimetrem, a také proud I, který cirkuluje vodičem..
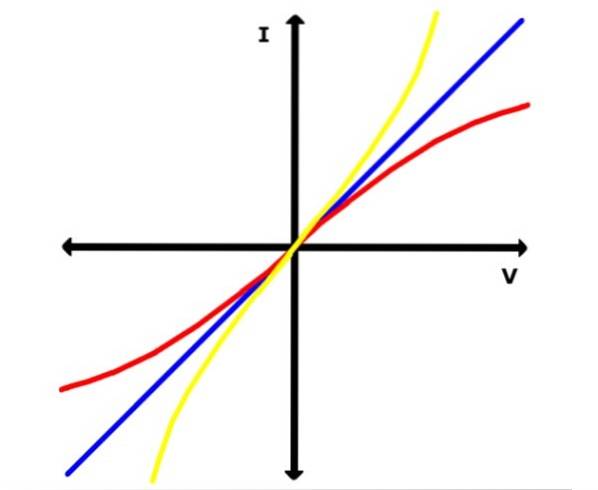
Dvojice hodnot V a I jsou zaznamenány v tabulce a je s nimi sestaven graf na milimetrovém papíru. Pokud je výsledná křivka přímka, materiál je ohmický, ale pokud se jedná o jakoukoli jinou křivku, materiál je neohmický.
V prvním případě lze určit sklon vedení, který je ekvivalentní odporu R vodiče nebo jeho inverzi, vodivosti.
Na obrázku níže představuje modrá čára jeden z těchto grafů pro ohmický materiál. Mezitím jsou žluté a červené křivky vyrobeny z neohmických materiálů, jako je například polovodič..
Hydraulická analogie Ohmova zákona
Je zajímavé vědět, že elektrický proud v Ohmově zákoně se chová podobně jako voda protékající trubkou. Anglický fyzik Oliver Lodge jako první navrhl simulaci chování proudu pomocí prvků hydrauliky.
Například potrubí představují vodiče, protože voda cirkuluje skrz ně a nosiče proudu skrz druhé. Pokud je v potrubí zúžení, je průchod vody obtížný, takže by to odpovídalo elektrickému odporu.
Rozdíl v tlaku na dvou koncích trubice umožňuje průtok vody, což poskytuje rozdíl ve výšce nebo vodní čerpadlo, a podobně rozdíl v potenciálu (baterie) je to, co udržuje náboj v pohybu., Což odpovídá průtoku nebo objem vody za jednotku času.
Pístové čerpadlo by hrálo roli zdroje střídavého napětí, ale výhodou nasazení vodního čerpadla je, že hydraulický okruh by byl tak uzavřen, stejně jako elektrický obvod musí být, aby mohl proud protékat.

Rezistory a spínače
Ekvivalent spínače v obvodu, byl by to kohout. Interpretuje se to takto: pokud je obvod otevřený (kohout uzavřen), proud, stejně jako voda, nemůže protékat.
Na druhou stranu, při sepnutém spínači (uzavírací kohout zcela otevřený) může proud i voda bez problémů protékat vodičem nebo potrubím.
Uzavírací kohout nebo ventil mohou také představovat odpor: když je kohoutek zcela otevřený, odpovídá to nulovému odporu nebo zkratu. Pokud se úplně zavře, je to jako mít obvod otevřený, zatímco částečně uzavřený, je to jako mít odpor určité hodnoty (viz obrázek 3).
Výcvik
- Cvičení 1
Je známo, že elektrická žehlička vyžaduje 2A při 120V, aby správně fungovala. Jaký je váš odpor??
Řešení
Vyřešit odpor z Ohmova zákona:
R = V / I = 120 V / 2 A = 60 Ω
- Cvičení 2
Drát o průměru 3 mm a délce 150 m má elektrický odpor 3,00 Ω při 20 ° C. Najděte odpor materiálu.
Řešení
Rovnice R = ρℓ / A je vhodné, proto je třeba nejprve najít průřezovou plochu:
A = π(D / 2)dva = π (3 x 10-3 m / 2)dva = 4,5π x 10 -6 mdva
Nakonec při střídání získáte:
ρ = A.R / ℓ = 4,5π x 10 -6 mdva x 3 Ω / 150 m = 2,83 x 10 -7 Ω.m
Reference
- Resnick, R. 1992. Fyzika. Třetí rozšířené vydání ve španělštině. Volume 2. Compañía Editorial Continental S.A. autor: C.V.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14th. Ed. Volume 2. 817-820.
- Serway, R., Jewett, J. 2009. Fyzika pro vědu a inženýrství s moderní fyzikou. 7. vydání. Svazek 2. Cengage Learning. 752-775.
- Tippens, P. 2011. Fyzika: koncepty a aplikace. 7. vydání. Mcgraw kopec.
- Sevillská univerzita. Katedra aplikované fyziky III. Hustota a intenzita proudu. Obnoveno z: us.es.
- Walker, J. 2008. Fyzika. 4. vyd. Pearson. 725-728



Zatím žádné komentáře