Zákony exponentů (s příklady a vyřešenými cvičeními)

The zákony exponentů jsou ty, které se vztahují na toto číslo, které udává, kolikrát musí být základní číslo vynásobeno samo. Exponenty jsou také známé jako mocniny. Posílení je matematická operace tvořená základnou (a), exponentem (m) a silou (b), která je výsledkem operace.

Exponenty se obecně používají, když se používají velmi velká množství, protože to nejsou nic jiného než zkratky, které představují násobení stejného počtu v určitém počtu opakování. Exponenti mohou být pozitivní i negativní.

Rejstřík článků

• 1 Vysvětlení zákonů exponentů
  • 1.1 První zákon: síla exponenta rovna 1
  • 1.2 Druhý zákon: síla exponentu rovna 0
  • 1.3 Třetí zákon: záporný exponent
  • 1.4 Čtvrtý zákon: znásobení pravomocí se stejnou základnou
  • 1.5 Pátý zákon: rozdělení pravomocí se stejnou základnou
  • 1.6 Šestý zákon: znásobení pravomocí na různých základnách
  • 1.7 Sedmý zákon: rozdělení pravomocí na různých základnách
  • 1.8 Osmý zákon: síla moci
  • 1.9 Devátý zákon: zlomkový exponent
• 2 Vyřešená cvičení
  • 2.1 Cvičení 1
  • 2.2 Cvičení 2
• 3 Odkazy

Vysvětlení zákonů exponentů

Jak je uvedeno výše, exponenty jsou zkratkovou formou, která představuje několikanásobné násobení čísel, přičemž exponent se vztahuje pouze k číslu vlevo. Například:

dva³ = 2 * 2 * 2 = 8

V takovém případě je číslo 2 základem síly, která se třikrát znásobí, jak ukazuje exponent, umístěný v pravém horním rohu základny. Existují různé způsoby, jak číst výraz: 2 zvýšeno na 3 nebo také 2 zvýšeno na krychli.

Exponenty také označují počet případů, kdy je lze rozdělit, a pro odlišení této operace od násobení má exponent před sebou znaménko minus (-) (je záporné), což znamená, že exponent je ve jmenovateli zlomek. Například:

dva^{- 4} = 1/2 * 2 * 2 * 2 = 1/16

To by nemělo být zaměňováno s případem, kdy je základna záporná, protože to bude záviset na tom, zda je exponent lichý nebo sudý, aby určil, zda bude síla kladná nebo záporná. Musíte tedy:

- Je-li exponent sudý, bude síla kladná. Například:

(-7)^dva = -7 _* -7 = 49.

- Pokud je exponent lichý, bude síla záporná. Například:

(-dva)⁵ = (-2) * (- 2) * (- 2) * (- 2) * (- 2) = - 32.

Existuje speciální případ, kdy je-li exponent roven 0, síla je rovna 1. Existuje také možnost, že základna je 0; v takovém případě bude síla v závislosti na exponentovi neurčitá nebo ne.

K provádění matematických operací s exponenty je nutné dodržovat několik pravidel nebo norem, které usnadňují hledání řešení těchto operací.

První zákon: síla exponenta rovna 1

Když je exponent 1, výsledkem bude stejná hodnota základny: a¹ = a.

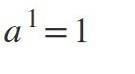
Příklady

9¹ = 9.

22¹ = 22.

895¹ = 895.

Druhý zákon: mocnost exponentů rovna 0

Je-li exponent 0, je-li základna nenulová, bude výsledek: a⁰ = 1.

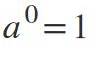
Příklady

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Třetí zákon: záporný exponent

Vzhledem k tomu, že exponát je záporný, výsledkem bude zlomek, kde síla bude jmenovatelem. Pokud je například m kladné, pak a^-m = 1 / rok^m.

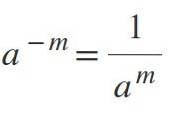
Příklady

- 3^-1 = 1/3.

- 6^-dva = 1/6^dva = 1/36.

- 8^-3 = 1/8³ = 1/512.

Čtvrtý zákon: znásobení pravomocí se stejnou základnou

Chcete-li znásobit mocniny, kde jsou báze stejné a odlišné od 0, zůstává základna a jsou přidány exponenty: a^m _* naⁿ = a^{m + n}.    

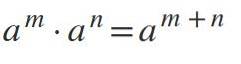
Příklady

- 4⁴ _* 4³ = 4^{4 + 3} = 4⁷

- 8¹ _* 8⁴ = 8^{1 + 4} = 8⁵

- dva^dva _* dva⁹ = 2^{2 + 9} = 2^jedenáct

Pátý zákon: dělba moci se stejným základem

Chcete-li rozdělit mocniny, ve kterých jsou základny stejné a odlišné od 0, je základna zachována a exponenty jsou odečteny následujícím způsobem: a^m / doⁿ = a^m-n.    

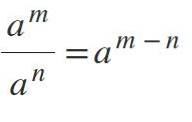
Příklady

- 9^dva / 9¹ = 9 ^{(dvacet jedna)} = 9¹.

- 6^patnáct / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Šestý zákon: znásobení pravomocí na různých základnách

V tomto zákoně je opak toho, co je vyjádřeno ve čtvrtém; to znamená, že pokud máte různé báze, ale se stejnými exponenty, základy se znásobí a exponent se zachová: a^m _* b^m = (a_*b) ^m.

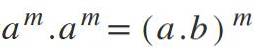
Příklady

- 10^dva _* dvacet^dva = (10 _* dvacet)^dva = 200^dva.

- Čtyři pět^jedenáct _* 9^jedenáct = (45 * 9)^{11 =} 405^jedenáct.

Dalším způsobem, jak reprezentovat tento zákon, je situace, kdy je násobení povýšeno na mocninu. Exponent tedy bude patřit ke každému z termínů: (a_*b)^m= a^m_* b^m.

Příklady

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Sedmý zákon: rozdělení pravomocí na odlišném základě

Pokud máte různé základny, ale se stejnými exponenty, rozdělte základny a exponent ponechejte: a^m / b^m = (a / b)^m.

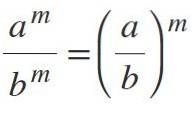
Příklady

- 30³ / dva³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5,5⁴.

Podobně, když se dělení zvýší na mocninu, bude exponent patřit do každého z termínů: (a / b) ^m = a^m / b^m.

Příklady

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)^dva = 25^dva / 5^dva = 5^dva.

Existuje případ, kdy je exponent záporný. Poté, aby byla kladná, je hodnota čitatele obrácena s hodnotou jmenovatele, a to následovně:

- (a / b)^-n = (b / a)ⁿ = bⁿ / doⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Osmý zákon: moc moci

Máte-li mocninu, která je pozvednuta na jinou mocninu - tedy dva exponenty současně -, základ se zachová a exponenty se násobí: (a^m)ⁿ= a^{m *n}.

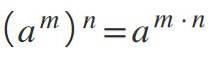
Příklady

- (8³)^dva = 8 ^{(3 * 2)} = 8⁶.

- (13⁹)³ = 13 ^{(9 * 3)} = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Devátý zákon: zlomkový exponent

Pokud má mocnina zlomek jako exponent, vyřeší se to transformací na n-tý kořen, kde čitatel zůstane jako exponent a jmenovatel představuje index kořene:

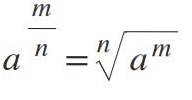
Příklad

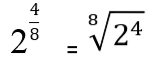
Vyřešená cvičení

Cvičení 1

Vypočítejte operace mezi mocnostmi, které mají různé základny:

dva⁴ _* 4⁴ / 8^dva.

Řešení

Při použití pravidel exponentů se základy v čitateli znásobí a exponent se zachová, například takto:

dva⁴ _* 4⁴ / 8^dva= (2_*4)⁴ / 8^dva  = 8⁴ / 8^dva

Nyní, protože máme stejné báze, ale s různými exponenty, je základ zachován a exponenty jsou odečteny:

 8⁴ / 8^dva = 8^{(4 - 2)} = 8^dva

Cvičení 2

Vypočítejte operace mezi mocnostmi získanými na jinou mocninu:

(3^dva)³ _* (dva _* 6⁵)^-dva _* (dva^dva)³

Řešení

Při uplatňování zákonů musíte:

(3^dva)³ _* (dva _* 6⁵)^-dva _* (dva^dva)³

= 3⁶ _* dva^-dva _* dva^-10 _* dva⁶

= 3⁶ _* dva^{(-2) + (- 10)} _* dva⁶

= 3⁶ _*  dva^-12 _* dva⁶

= 3⁶ _* dva^{(-12) + (6)}

= 3⁶ _* dva⁶

= (3_*dva)⁶

= 6⁶

= 46 656

Reference

1. Aponte, G. (1998). Základní základy matematiky. Pearson Education.
2. Corbalán, F. (1997). Matematika aplikovaná na každodenní život.
3. Jiménez, J. R. (2009). Matematika 1 SEP.
4. Max Peters, W. L. (1972). Algebra a trigonometrie.
5. Rees, P. K. (1986). Reverte.