
Metoda nejmenších čtverců, cvičení a k čemu slouží
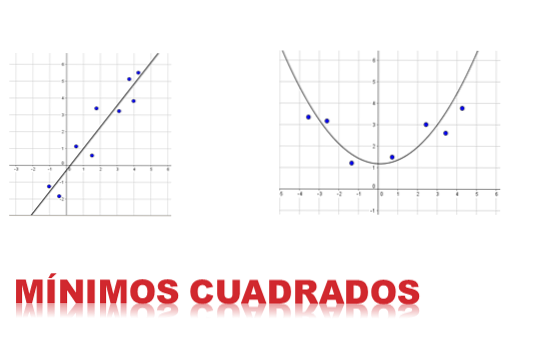
Metoda Nejmenší čtverce je to jedna z nejdůležitějších aplikací při aproximaci funkcí. Cílem je najít křivku tak, aby vzhledem k sadě uspořádaných párů tato funkce nejlépe aproximovala data. Funkce může být přímka, kvadratická křivka, kubický atd..
Myšlenka metody spočívá v minimalizaci součtu čtverců rozdílů v souřadnici (složka Y) mezi body generovanými zvolenou funkcí a body patřícími do datové sady.
Rejstřík článků
- 1 Metoda nejmenších čtverců
- 2 Vyřešená cvičení
- 2.1 Cvičení 1
- 2.2 Cvičení 2
- 3 K čemu slouží?
- 4 Odkazy
Metoda nejmenších čtverců
Před uvedením metody si musíme nejprve ujasnit, co znamená „lepší přístup“. Předpokládejme, že hledáme přímku y = b + mx, která nejlépe představuje množinu n bodů, jmenovitě (x1, y1), (x2, y2)…, (xn, yn).
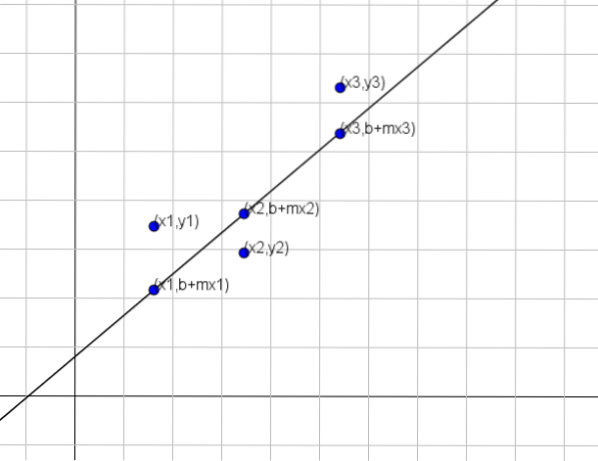
Jak je znázorněno na předchozím obrázku, pokud by proměnné xay byly vztaženy k přímce y = b + mx, pak pro x = x1 by odpovídající hodnota y byla b + mx1. Tato hodnota se však liší od skutečné hodnoty y, což je y = y1.
Pamatujte, že v rovině je vzdálenost mezi dvěma body dána následujícím vzorcem:
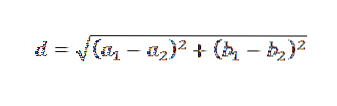
S ohledem na tuto skutečnost se zdá logické použít k výběru způsobu přímky y = b + mx, která nejlépe odpovídá daným údajům, jako kritérium výběr přímky, která minimalizuje součet čtverců vzdáleností mezi body a přímka.
Protože vzdálenost mezi body (x1, y1) a (x1, b + mx1) je y1- (b + mx1), náš problém se redukuje na hledání čísel m a b tak, aby následující součet byl minimální:
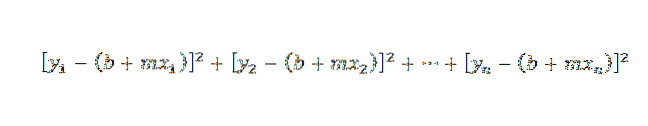
Přímka, která splňuje tuto podmínku, se označuje jako „aproximace čáry nejmenších čtverců k bodům (x1, y1), (x2, y2), ..., (xn, yn)“.
Jakmile je problém získán, zbývá už jen zvolit metodu k nalezení aproximace nejmenších čtverců. Pokud jsou body (x1, y1), (x2, y2),…, (xn, yn) všechny na přímce y = mx + b, měli bychom mít, že jsou kolineární y:
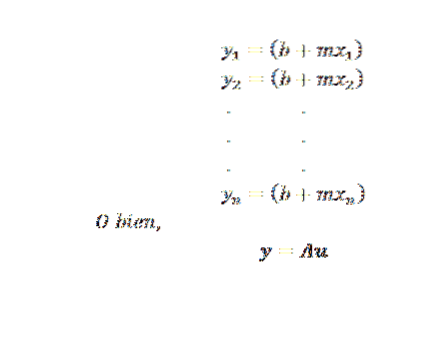
V tomto výrazu:
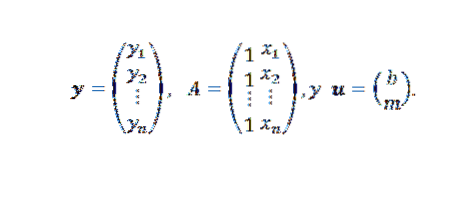
A konečně, pokud body nejsou kolineární, pak y-Au = 0 a problém lze přeložit do nalezení vektoru u takového, že euklidovská norma je minimální.
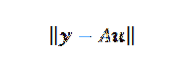
Nalezení minimalizačního vektoru u není tak obtížné, jak si možná myslíte. Protože A je matice nx2 a u je matice 2 × 1, máme, že vektor Au je vektor v Rn y patří k obrazu A, což je podprostor Rn s rozměrem ne větším než dva.
Budeme předpokládat, že n = 3, abychom ukázali, jak postupovat. Pokud n = 3, bude obraz A rovinou nebo přímkou, která prochází počátkem.
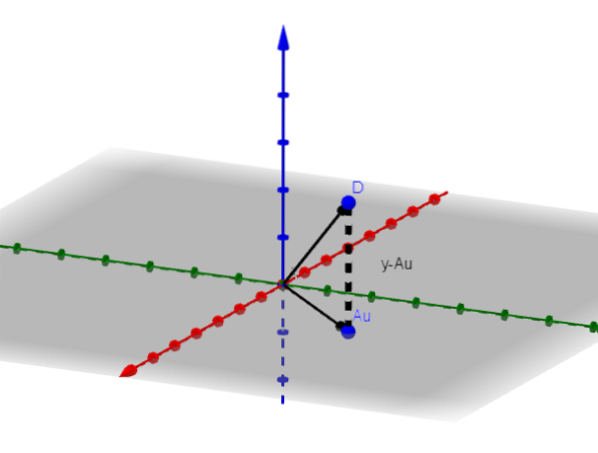
Nechť v je minimalizující vektor. Na obrázku pozorujeme, že y-Au je minimalizován, když je kolmý k obrazu A. To znamená, že pokud v je minimalizující vektor, pak se stane, že:
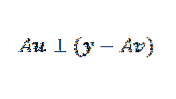
Poté můžeme výše uvedené vyjádřit tímto způsobem:
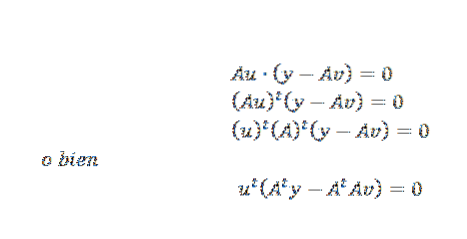
K tomu může dojít, pouze pokud:
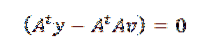
Nakonec řešení pro v máme:
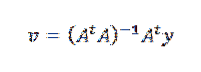
Je možné to udělat od AtA je invertibilní, pokud n bodů zadaných jako data nejsou kolineární.
Nyní, pokud bychom místo hledání řádku chtěli najít parabolu (jejíž výraz by byl ve tvaru y = a + bx + cxdva), což by bylo lepší přiblížení k n datovým bodům, postup by byl popsán níže.
Pokud by n datových bodů bylo v uvedené parabole, měli bychom:
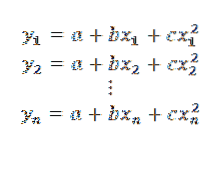
Později:
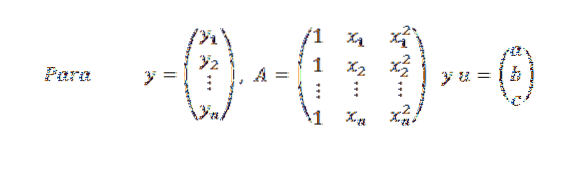
Podobně můžeme napsat y = Au. Pokud všechny body nejsou v parabole, máme, že y-Au se liší od nuly pro libovolný vektor u a náš problém je znovu: najděte vektor u v R3 tak, aby jeho norma || y-Au || být co nejmenší.
Opakováním předchozího postupu můžeme dojít k tomu, že hledaný vektor je:
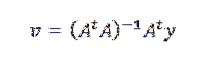
Vyřešená cvičení
Cvičení 1
Najděte přímku, která nejlépe odpovídá bodům (1,4), (-2,5), (3, -1) a (4,1).
Řešení
Musíme:
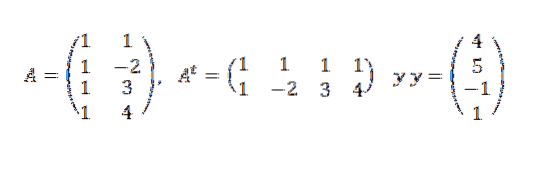
Později:
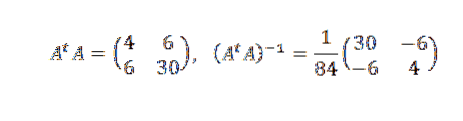
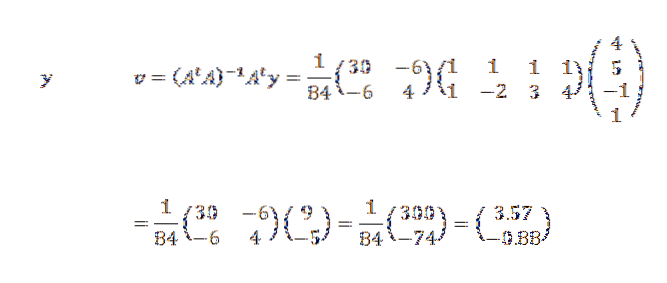
Proto jsme dospěli k závěru, že přímka, která nejlépe vyhovuje bodům, je dána vztahem:
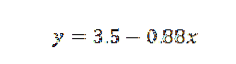
Cvičení 2
Předpokládejme, že předmět spadl z výšky 200 m. Jak klesá, jsou podniknuty následující kroky:
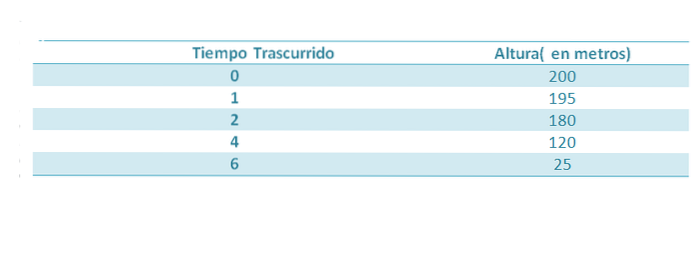
Víme, že výška zmíněného objektu je po uplynutí času t dána vztahem:
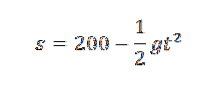
Pokud bychom chtěli získat hodnotu g, můžeme hledat parabolu, která je lepší aproximací pěti bodům uvedeným v tabulce, a tak bychom měli koeficient, který doprovází tdva bude přiměřená aproximace na (-1/2) g, pokud jsou měření přesná.
Musíme:
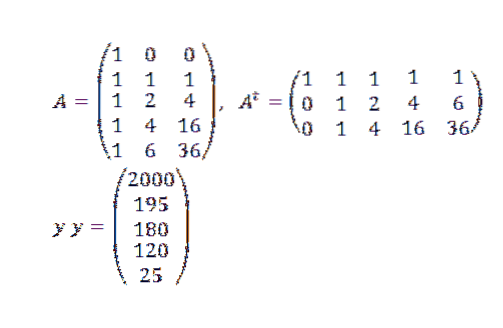
A později:
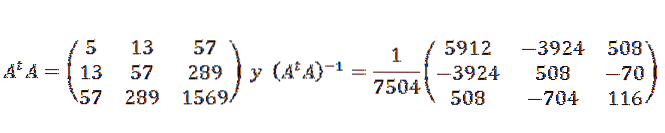

Datové body tedy zapadají do následujícího kvadratického výrazu:
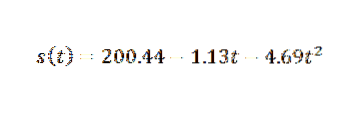
Musíte tedy:
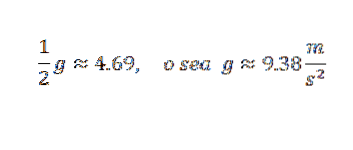
Jedná se o hodnotu, která je přiměřeně blízká korekci, což je g = 9,81 m / sdva. Abychom získali přesnější aproximaci g, bylo by nutné vycházet z přesnějších pozorování.
K čemu to je?
V problémech, které se vyskytují v přírodních nebo společenských vědách, je vhodné psát vztahy, které existují mezi různými proměnnými, pomocí nějakého matematického výrazu.
Například v ekonomii můžeme spojit náklady (C), příjem (I) a zisky (U) pomocí jednoduchého vzorce:
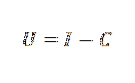
Ve fyzice můžeme spojit zrychlení způsobené gravitací, čas, kdy předmět padal, a výšku objektu podle zákona:
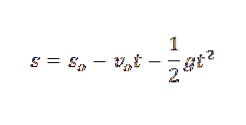
V předchozím výrazu snebo je počáteční výška uvedeného objektu a vnebo je jeho počáteční rychlost.
Nalezení takových vzorců však není snadný úkol; obvykle je na profesionálovi ve službě, aby pracoval s velkým množstvím dat a opakovaně provedl několik experimentů (aby ověřil, že získané výsledky jsou konstantní), aby našel vztahy mezi různými daty.
Běžným způsobem, jak toho dosáhnout, je reprezentovat data získaná v rovině jako body a hledat spojitou funkci, která tyto body optimálně aproximuje..
Jedním ze způsobů, jak najít funkci, která „nejlépe aproximuje“ daná data, je metoda nejmenších čtverců..
Kromě toho, jak jsme také viděli na cvičení, můžeme díky této metodě získat poměrně blízké aproximace fyzikálních konstant.
Reference
- Charles W Curtis Lineární algebra. Springer-Velarg
- Kai Lai Chung. Teorie základní stability se stochastickými procesy. Springer-Verlag New York Inc.
- Richar L Burden a J. Douglas Faires. Numerická analýza (7ed). Thompson učení.
- Stanley I. Grossman. Aplikace lineární algebry. MCGRAW-HILL / INTERAMERICANA DE MEXICO
- Stanley I. Grossman. Lineární algebra. MCGRAW-HILL / INTERAMERICANA DE MEXICO



Zatím žádné komentáře