The Bohrův atomový model je koncepce dánského fyzika Nielse Bohra (1885-1962) o struktuře atomu, publikovaná v roce 1913. V Bohrově atomu zaujímají elektrony kolem jádra pouze určité povolené oběžné dráhy, a to díky omezení tzv. kvantování.
Pro Bohra obraz atomu jako miniaturní sluneční soustavy s elektrony obíhajícími kolem jádra nebyl zcela v souladu se skutečností, že při zrychlení elektrické náboje vyzařují energii..
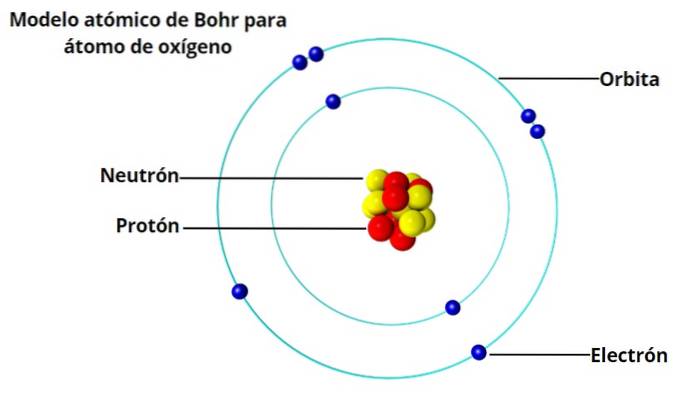
Takový atom by nebyl stabilní, protože by se dříve nebo později zhroutil, protože elektrony by spirálovitě směřovaly k jádru. A do té doby byly charakteristické světelné vzorce, které vodík a další plyny emitují při zahřátí, známé už 50 let..
Vzor nebo spektrum se skládá z řady jasných čar určitých velmi specifických vlnových délek. A atom vodíku se nezhroutí vyzařováním světla.
Aby vysvětlil, proč je atom stabilní, přestože je schopen vyzařovat elektromagnetickou energii, Bohr navrhl, aby moment hybnosti mohl přijímat pouze určité hodnoty, a tedy i energii. To je míněno kvantizací.
Přijme-li, že energie byla kvantována, elektron bude mít potřebnou stabilitu, aby se nehnal směrem k jádru ničícímu atom..
A atom vyzařuje světelnou energii pouze tehdy, když elektron přechází z jedné dráhy na druhou, vždy v diskrétních množstvích. Tímto způsobem je vysvětlena přítomnost emisních vzorců ve vodíku..
Bohr tedy složil vizi atomu integrací známých konceptů z klasické mechaniky s nově objevenými, jako je Planckova konstanta, foton, elektron, atomové jádro (Rutherford byl Bohrův mentor) a výše uvedená spektra emise.
Rejstřík článků
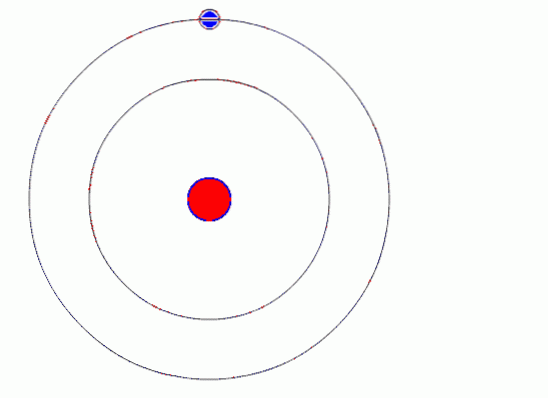
Bohrův atomový model předpokládá, že se elektron pohybuje na kruhové dráze kolem jádra působením Coulombovy elektrostatické přitažlivé síly a navrhuje, aby se kvantovala moment hybnosti elektronu.
Podívejme se, jak integrovat oba pojmy v matematické formě:
Nechť L je velikost momentu hybnosti, m hmotnost elektronu, v rychlost elektronu, ar poloměr oběžné dráhy. Pro výpočet L máme:
L = m⋅r⋅v
Bohr navrhl, že L se rovná celočíselným násobkům konstanty h / 2π, kde h je Planckova konstanta, představil před krátkou dobou fyzik Max Planck (1858-1947) při řešení problému energie emitované černým tělesem, teoretický objekt, který absorbuje veškeré dopadající světlo.
Jeho hodnota je h = 6,626 × 10-34 J ・ s, zatímco h / 2π je označeno jako ħ, co se čte "H bar".
Moment hybnosti L tedy zůstává:
m⋅r⋅v = nħ, s n = 1,2, 3 ...
A z této podmínky se odvodí poloměry oběžných drah povolených pro elektron, jak uvidíme níže.
V následujícím budeme předpokládat nejjednodušší z atomů: vodík, který se skládá z jediného protonu a elektronu, oba s nábojem o velikosti e.
Dostředivá síla, která udržuje elektron na jeho kruhové dráze, je poskytována elektrostatickou přitažlivostí, jejíž velikost F je:
F = kedva/ rdva
Kde k je elektrostatická konstanta Coulombova zákona ar vzdálenost elektron-proton. S vědomím, že v kruhovém pohybu dostředivé zrychlení přiC je dáno poměrem mezi druhou mocninou rychlosti a vzdáleností r:
naC = vdva / r
Podle druhého Newtonova zákona je čistá síla součinem hmotnosti m a zrychlení:
mvdva/ r = kedva/ rdva
Zjednodušením poloměru r získáme:
m⋅vdvar = kedva
Kombinací tohoto výrazu s výrazem momentu hybnosti máme systém rovnic, daný:
1) mvdvar = kedva
2) r = n ħ/ mv
Cílem je vyřešit systém a určit r, poloměr povolené oběžné dráhy. K odpovědi vede malá elementární algebra:
r = (nħ)dva / k⋅m⋅edva
S n = 1, 2, 3, 4, 5 ...
Pro n = 1 máme nejmenší z poloměrů, tzv Bohrův poloměr donebo s hodnotou 0,529 × 10-10 m. Poloměry ostatních oběžných drah jsou vyjádřeny jako nanebo.
Tímto způsobem Bohr zavádí hlavní kvantové číslo n, konstatuje, že povolené poloměry jsou funkcí Planckovy konstanty, elektrostatické konstanty a hmotnosti a náboje elektronu.
Bohr dovedně kombinuje newtonovskou mechaniku s novými objevy, které se neustále vyskytovaly během druhé poloviny devatenáctého a počátku dvacátého století. Mezi nimi revoluční koncept „kvanta“, o kterém sám Planck tvrdil, že není příliš přesvědčen.
Díky své teorii dokázal Bohr uspokojivě vysvětlit řadu ve vodíkovém spektru a předpovědět emise energie v ultrafialovém a infračerveném rozsahu, které dosud nebyly pozorovány..
Můžeme shrnout jeho postuláty následovně:
Elektron se točí kolem jádra na stabilní kruhové dráze s rovnoměrným kruhovým pohybem. Pohyb je způsoben elektrostatickou přitažlivostí, kterou na něj jádro působí.
Moment hybnosti elektronu je kvantován podle výrazu:
L = mvr = nħ
Kde n je celé číslo: n = 1, 2, 3, 4 ..., což vede k tomu, že elektron může být pouze na určitých definovaných drahách, jejichž poloměry jsou:
r = (n ħ)dva / k m edva
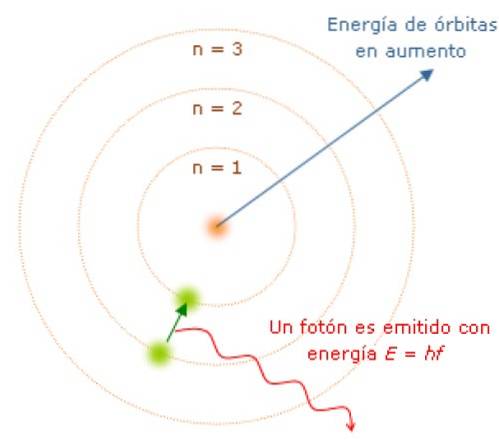
Jelikož je moment hybnosti kvantován, je tomu tak i u energie E. Je možné ukázat, že E je dáno vztahem:
Elektronový volt, nebo eV, je další jednotka energie, široce používaná v atomové fyzice. Záporné znaménko v energii zajišťuje stabilitu oběžné dráhy, což naznačuje, že k oddělení elektronu od této polohy bude třeba provést práci..
Když je elektron na své oběžné dráze, neabsorbuje ani nevyzařuje světlo. Ale když skočí z oběžné dráhy s vyšší energií na nižší, udělá to..
Frekvence f vyzařovaného světla závisí na rozdílu mezi energetickými hladinami oběžných drah:
E = hf = Epočáteční - Efinále
Bohrův model má určitá omezení:
-Úspěšně se aplikuje pouze na atom vodíku. Pokusy o jeho aplikaci na složitější atomy byly neúspěšné.
-Neodpovídá, proč jsou některé dráhy stabilní a jiné ne. Skutečnost, že energie v atomu byla kvantována, fungovala velmi dobře, ale model neposkytl důvod, a to bylo něco, co vědcům způsobovalo nepohodlí..
-Dalším důležitým omezením je to, že nevysvětlilo další čáry vyzařované atomy v přítomnosti elektromagnetických polí (Zeemanův efekt a Starkův efekt). Nebo proč byly některé linie spektra intenzivnější než jiné.
-Bohrův model také nezohledňuje relativistické efekty, které je nutné vzít v úvahu, protože bylo experimentálně zjištěno, že elektrony jsou schopné dosáhnout rychlostí docela blízkých rychlosti světla ve vakuu..
-Předpokládá, že je možné přesně znát polohu a rychlost elektronu, ale ve skutečnosti se vypočítá pravděpodobnost, že elektron zaujme určitou polohu.
Navzdory svým omezením byl model v té době velmi úspěšný, a to nejen pro integraci nových objevů s již známými prvky, ale také proto, že vyvolal nové otázky, které jasně ukazují, že cesta k uspokojivému vysvětlení atomu spočívala v kvantové mechanice..
Schrödingerův atomový model.
Atomový model de Broglie.
Chadwickův atomový model.
Heisenbergův atomový model.
Perrinův atomový model.
Thomsonův atomový model.
Daltonův atomový model.
Atomový model Dirac Jordan.
Atomový model Demokrita.
Atomový model Leucippus.
Sommerfeldův atomový model.
Aktuální atomový model.
Zatím žádné komentáře