Částice má kruhový pohyb jednotný (M.C.U.), když jeho trajektorie je obvod a také po ní cestuje konstantní rychlostí. Mnoho druhů, například součásti strojů a motorů, má tento druh pohybu, mezi nimiž vynikají pevné disky počítačů, lopatky ventilátorů, hřídele a mnoho dalších věcí..
Rovnoměrný kruhový pohyb je také dobrou aproximací pro pohyb některých nebeských těles, jako je Země. Ve skutečnosti je oběžná dráha Země eliptická, jak naznačují Keplerovy zákony. Excentricita oběžné dráhy je však malá a jako první aproximaci ji lze považovat za kruhovou, což zjednodušuje některé výpočty, například zjištění rychlosti Země, když se pohybuje kolem Slunce..
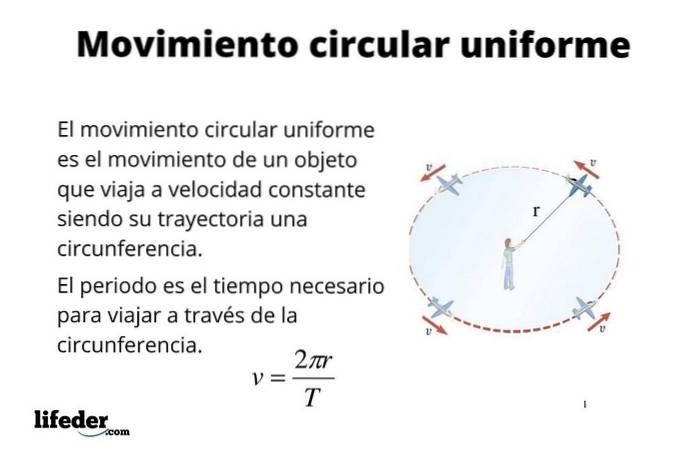
Při popisu rovnoměrného kruhového pohybu se používají stejné parametry jako v přímém pohybu, a to: poloha, posunutí, čas, rychlost a zrychlení..
Akcelerace? Ano, rovnoměrný kruhový pohyb je zrychlen, i když jeho rychlost proti být konstantní. Je to proto, že rychlost proti, což je vektor, a proto je tučně a neustále mění svůj směr při otáčení objektu nebo částice. Jakákoli změna v proti je produkováno zrychlením, které, jak bude vidět, je směrováno do středu kruhové dráhy.
Jednotný kruhový pohyb je pohyb v rovině xy, jedná se tedy o pohyb ve dvou dimenzích. Je však možné to pohodlněji vyjádřit pomocí úhlu θ, který zametá částice, měřeno vzhledem k vodorovné ose nebo jiné vhodné referenční ose..
I když se jedná o rozšířený objekt, jeho částice vždy zametají stejný úhel, i když mají různé souřadnice. (x, y).
Rejstřík článků
Vlastnosti rovnoměrného kruhového pohybu lze shrnout následovně:
-Dráha je obvod, jedná se tedy o pohyb v rovině.
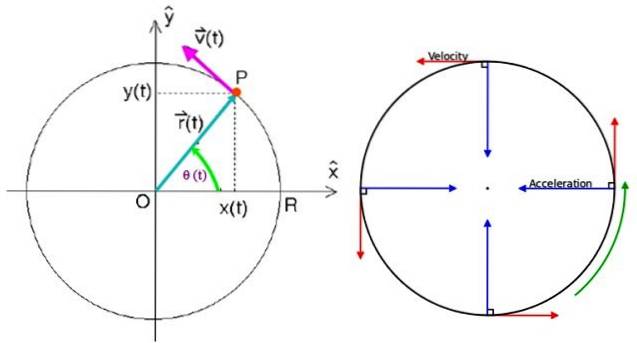
-Rychlost proti je konstantní, ale rychlost proti ne, protože neustále mění směr a směr, aby vyhověl otočení mobilu.
-Vektor rychlosti proti je vždy tangenciální k obvodu a kolmé k radiálnímu směru.
-Úhlová rychlost ω je konstantní.
-Navzdory jednotnosti existuje zrychlení, které vysvětluje tyto změny ve směru rychlosti. Toto zrychlení je dostředivé zrychlení.
-Dostředivé zrychlení a rychlost jsou navzájem kolmé.
-Jedná se o periodický nebo opakující se pohyb, proto jsou pro něj definovány periodické a frekvenční veličiny.
V tomto schématu je částice P rotující proti směru hodinových ručiček s MCU, podle směru a smyslu vektoru rychlosti proti tažené.
Pro určení vektoru polohy je nutné mít referenční bod a ideálním bodem je střed obvodu O, který se shoduje se středem kartézského souřadného systému v rovině xy.
Označuje se jako r (t) a je směrována od počátku do bodu P, kde se nachází částice. V daném okamžiku t se v kartézských souřadnicích píše jako:
r (t) = x (t) i + a (t) j
Kde i Y j jsou jednotkové vektory kolmé ve směrech X a Y resp. Z grafu je vidět, že vektorový modul r (t) vždy stojí za to R, poloměr obvodu. Pokud je θ utvořený úhel r s vodorovnou osou je poloha rovna také:
r (t) = [Rcos θ(t)] i +[Rsen θ(t)] j
Úhel, který tvoří r (t) s vodorovnou osou je středový úhel a jeho hodnota je:
θ = s / R
Kde s je uražený oblouk obvodu a R poloměr. Uvedený úhel θ je funkce času, takže se dá psát θ = θ (t), volání úhlová poloha.
Protože rychlost je konstantní, částice popisuje stejné úhly ve stejných časech a analogicky s rovnoměrným přímočarým pohybem se píše:
θ = θ (t) = θnebo + ωt
Tady θnebo je počáteční úhel měřený v radiánech vzhledem k referenční ose, může to být 0 nebo jakákoli hodnota a ω je úhlová rychlost.
Úhlová rychlost je první derivací úhlové polohy a označuje se jako ω. Jeho hodnota je konstantní pro rovnoměrný kruhový pohyb, protože stejné úhly jsou zameteny ve stejných časech. Jinými slovy:
Jednotky lineární rychlosti v rovnoměrném kruhovém pohybu jsou stejné jako u lineárního pohybu: m / s (v mezinárodním systému SI), km / h, cm / s a další..
Na obrázku níže je částice pohybující se po obvodu ve směru hodinových ručiček konstantní rychlostí. To znamená, že vektor rychlosti má vždy stejný modul, ale mění směr tak, aby vyhovoval obvodu.
Jakákoli změna rychlosti má za následek zrychlení, které je podle definice:
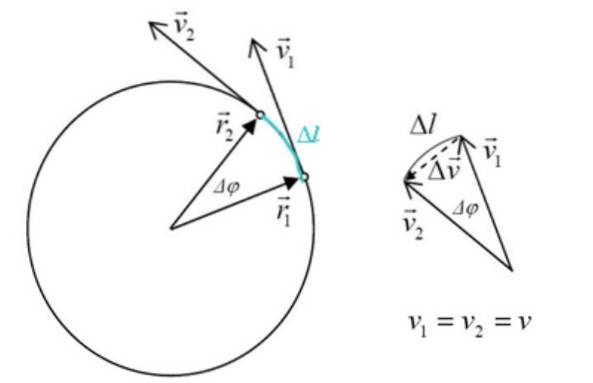
Trojúhelník tvořený protidva, proti1 a Δproti je podobný trojúhelníku po stranách rdva, r1 a Δl, kde Δφ je středový úhel. Veličiny rdva Y r1 jsou stejné, takže:
rdva = r1 = r
Pak z obou trojúhelníků máme tyto vztahy pro úhel:
Δφ = Δr / r; Δφ = Δv / v
Tučný typ není nutný, protože míra úhlu závisí na velikostech těchto vektorů. Odpovídající předchozím výrazům vyplývá, že:
Jelikož se kruhový pohyb opakuje, je definována perioda T stejně jako čas potřebný k úplnému otočení mobilu. Vzhledem k tomu, že délka obvodu poloměru R je 2πR, úhel zametaný v radiánech při plném otočení je 2π radiány a vyžaduje čas T, úhlová rychlost je:
ω = 2π / T
T = 2π / ω
Perioda rovnoměrného kruhového pohybu se v mezinárodním systému měří v sekundách.
Frekvence F je počet otáček za jednotku času a je převrácený nebo inverzní k období:
f = n / t = 1 / T.
Jednotkou frekvence v mezinárodním systému je s-1.
Mnoho objektů se otáčí a vytváří různé efekty: kola, disky a turbíny. Jakmile je dosaženo provozní rychlosti, otáčení se obvykle provádí konstantní rychlostí. Kruhový pohyb je v každodenním životě tak běžný, že na něj téměř nikdy nemyslíte, takže zde uvádíme několik příkladů, které to velmi dobře ilustrují:
Země a další planety sluneční soustavy se pohybují eliptickými trajektoriemi malé výstřednosti, s výjimkou Merkuru, což znamená, že při první aproximaci lze předpokládat, že jejich pohyb je rovnoměrný kruhový.
Díky tomu máte dobrou představu o rychlosti překladu kolem Slunce, protože v případě Země je známá doba pohybu: jeden rok nebo 365 dní..
Částice, které rotují na okraji starého gramofonu nebo lopatky ventilátoru, sledují rovnoměrný kruhový pohyb, jakmile zařízení dosáhne rychlosti přehrávání.
Hubblův kosmický dalekohled obíhá Zemi rychlostí přibližně 7550 m / s.
Pračky provádějí odstřeďování, při kterém se prádlo stlačí, což spočívá v otáčení bubnu nádoby vysokou rychlostí. Sušičky se také po určitou dobu otáčejí rovnoměrným kruhovým pohybem..
Centrifugace se také používá v laboratořích k oddělení sloučenin, a tím k oddělení jejich složek rozdílem v hustotách. Kdykoli mluvíme o odstřeďování, dochází k kruhovému pohybu, který je alespoň na čas rovnoměrný.
Mnoho zahradních postřikovačů se otáčí konstantní rychlostí, takže je půda zavlažována rovnoměrně..
Například při hodu kladivem, což je olympijská disciplína, sportovec točí kovovou kouli silou pomocí ocelového lana připevněného k rukojeti. Cílem je poslat míč co nejdále, ale bez opuštění určité oblasti.
Částice se pohybuje v obvodu o poloměru 2 m konstantní rychlostí v = 8 m / s, proti směru hodinových ručiček. Zpočátku byla částice uvnitř r = +2 j m. Vypočítat:
a) Úhlová rychlost ω
b) Jeho úhlová poloha θ (t)
c) Období pohybu
d) Dostředivé zrychlení.
e) Poloha částice po průchodu t = π / 4 s
Ze vzorce v = Rω vyplývá, že:
ω = v / R = (8 m / s) / 2m = 4rad ∙ s-1
Vezmeme-li kladnou osu x jako referenční osu, je částice zpočátku v 90 ° = π / 2 radiánech vzhledem k uvedené ose, protože tvrzení říká, že počáteční poloha je +2 j m, to znamená, že částice je na y = 2 m, když začne pohyb následovat.
θ = θ (t) = θnebo + ωt = π / 2 + 4t
T = 2π / ω = 2π / 4 s = 0,5 π s
a = vdva / R = (8 m / s)dva / 2 m = 32 m / sdva
θ (t) = π / 2 + 4t → θ (π / 4) = π / 2 + 4 ∙ (π / 4) = 3π / 2 radiány
To znamená, že po této době je částice v poloze y = -2m j. Dává to smysl, protože t = π / 4 s je polovina periody, proto částice prošla 180 ° úhlem proti směru hodinových ručiček od své počáteční polohy a musí být právě v opačné poloze.
Zatím žádné komentáře