
Konjugujte příklady vnitřních a vnějších úhlů, cvičení
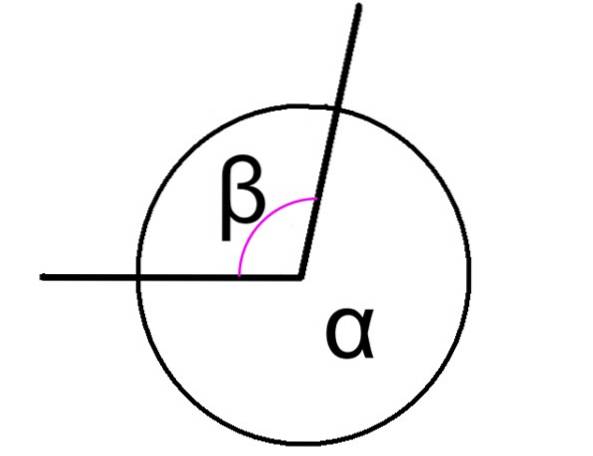
The konjugované úhly Jsou to ty, které po přidání dávají ve výsledku 360 °, bez ohledu na to, zda tyto úhly sousedí nebo ne. Na obrázku 1 jsou znázorněny dva úhly konjugátu, označené jako α a β.
V tomto případě mají úhly α a β na obrázku společný vrchol a jejich strany jsou společné, proto sousedí. Vztah mezi nimi je vyjádřen takto:
α + β = 360 °
Na druhou stranu uvažujme nyní o dvou rovnoběžných liniích proříznutých sekánem, jejichž uspořádání je uvedeno níže:
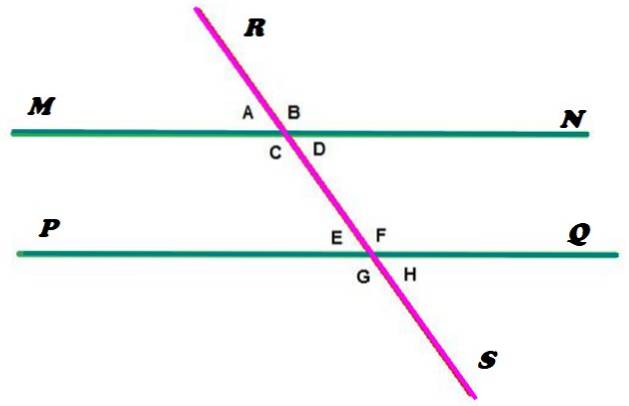
Řádky MN a PQ jsou rovnoběžné, zatímco přímka RS je sečna, protínající rovnoběžky ve dvou bodech. Jak je vidět, tato konfigurace určuje vznik 8 úhlů, které byly označeny malými písmeny.
Podle definice uvedené na začátku jsou úhly a, b, c a d konjugovány. A stejně jsou e, f, g a h, protože oba případy jsou pravdivé:
a + b + c + d = 360 °
Y
e + f + g + h = 360 °
U této konfigurace jsou dva úhly konjugovány, pokud jsou na stejné straně vzhledem k sekanční linii RS a oba jsou vnitřní nebo vnější. V prvním případě mluvíme o úhlech vnitřní konjugáty, zatímco ve druhém jsou úhly externí konjugáty.
Rejstřík článků
- 1 Příklady
- 2 Vnitřní úhly čtyřúhelníku
- 2.1 Příklady
- 3 cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Příklady
Na obrázku 2 jsou vnějšími úhly ty, které jsou mimo oblast ohraničenou přímkami MN a PQ, jsou to úhly A, B, G a H. Zatímco úhly, které leží mezi těmito dvěma čarami, jsou C, D, E a F.
Nyní je nutné analyzovat, které úhly jsou nalevo a které napravo od secantu.
Nalevo od RS jsou úhly A, C, E a G. A napravo jsou úhly B, D, F a H.
Okamžitě pokračujeme v určování dvojic úhlových konjugátů podle definice uvedené v předchozí části:
-A a G, vnější a nalevo od RS.
-D a F, vnitřní a napravo od RS.
-B a H, vnější a napravo od RS.
-C a E, vnitřní a nalevo od RS.
Vlastnost konjugovaných úhlů mezi rovnoběžnými čarami
Konjugované úhly mezi rovnoběžnými čarami jsou doplňkové, to znamená, že jejich součet se rovná 180 °. Tímto způsobem platí pro obrázek 2 následující:
A + G = 180 °
D + F = 180 °
B + H = 180 °
C + E = 180 °
Dvojice odpovídajících úhlů pro rovnoběžky
Jsou to ty, které jsou na stejné straně sekanční linie, nesousedí a jeden z nich je vnitřní a druhý je vnější. Je důležité si je vizualizovat, protože jejich míra je stejná, protože jsou vrcholem v opačném úhlu.
Vrátíme-li se k obrázku 2, odpovídající dvojice úhlů jsou označeny jako:
-A a E.
-C a G
-B a F
-D a H
Vnitřní úhly čtyřúhelníku
Čtyřstěny jsou čtyřstranné mnohoúhelníky, mezi nimi například čtverec, obdélník, lichoběžník, rovnoběžník a kosočtverec. Bez ohledu na jejich tvar, v kterémkoli z nich platí, že součet jejich vnitřních úhlů je 360 °, proto splňují definici uvedenou na začátku..
Podívejme se na několik příkladů čtyřúhelníků a na to, jak vypočítat hodnotu jejich vnitřních úhlů podle informací v předchozích částech:
Příklady
a) Tři z úhlů čtyřúhelníku měří 75 °, 110 ° a 70 °. Kolik by měl změřit zbývající úhel?
b) Najděte hodnotu úhlu ∠Q na obrázku 3 i.
c) Vypočítejte míru úhlu ∠A na obrázku 3 ii.
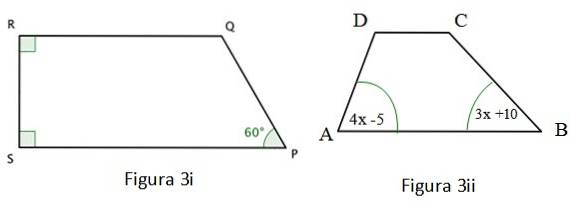
Řešení
Nechť α je chybějící úhel, je přesvědčeno, že:
α + 75 ° + 110 ° + 70 ° = 360 ° → α = 105 °
Řešení b
Obrázek 3i je zobrazen a lichoběžník a dva z jejích vnitřních úhlů jsou pravé, které byly v rozích označeny barevným čtvercem. U tohoto čtyřúhelníku se ověřuje toto:
∠R + ∠S + ∠P + ∠Q = 360 °; ∠S = ∠R = 90 °; ∠P = 60 °
Proto:
∠ Q = 2 x 90 ° + 60 ° = 240 °
Řešení c
Čtyřúhelník na obrázku 3 ii je také lichoběžník, pro který platí toto:
∠A + ∠B + ∠C + ∠D = 360 °
Proto:
4x -5 + 3x + 10 +180 = 360
7x + 5 = 180
x = (180 - 5) / 7
x = 25
K určení požadovaného úhlu ve výroku použijeme, že ∠A = 4x - 5. Z nahrazení dříve vypočítané hodnoty x vyplývá, že ∠A = (4 × 25) -5 = 95º
Výcvik
- Cvičení 1
S vědomím, že jeden ze zobrazených úhlů je 125 °, najděte míry 7 zbývajících úhlů na následujícím obrázku a zdůvodněte odpovědi.
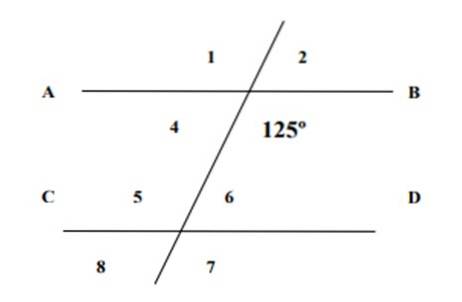
Řešení
Úhel 6 a úhel 125 ° jsou vnitřní konjugáty, jejichž součet je 180 °, podle vlastnosti konjugovaných úhlů, proto:
∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º
Na druhou stranu ∠6 a ∠8 jsou protilehlé úhly vrcholem, jehož míra je stejná. Proto 8 měří 55 °.
Úhel ∠1 je také opačný o vrchol na 125 °, pak můžeme potvrdit, že ∠1 = 125 °. Můžeme se také odvolat ke skutečnosti, že odpovídající dvojice úhlů mají stejnou míru. Na obrázku jsou to tyto úhly:
∠7 = 125 º
∠2 = ∠6 = 55 °
∠1 = ∠5 = 125º
∠4 = ∠8 = 55 °
- Cvičení 2
Hodnotu x najdete na následujícím obrázku a hodnoty všech úhlů:
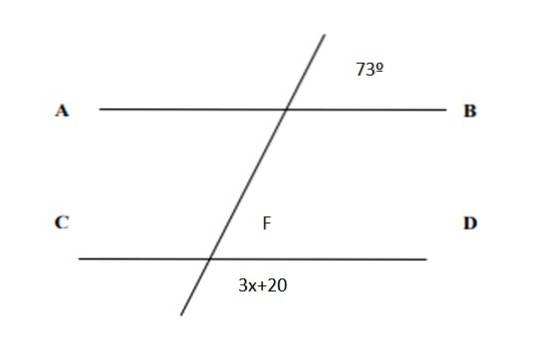
Řešení
Jelikož se jedná o odpovídající páry, vyplývá z toho, že F = 73 °. A na druhé straně je součet konjugovaných párů 180 °, proto:
3x + 20 ° + 73 ° = 180 °
3x = 180 ° - 73 ° -20 ° = 87
Nakonec je hodnota x:
x = 87/3 = 29
Pokud jde o všechny úhly, jsou uvedeny na následujícím obrázku:
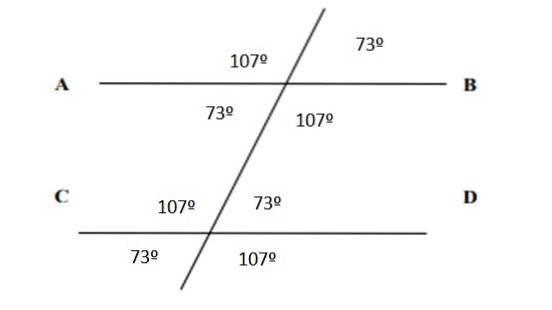
Reference
- Skupiny úhlů. Vysvětlení doplňkových, doplňkových a doplňkových úhlů. Obnoveno z: thisiget.com/
- Baldor, A. 1983. Geometrie letadla a kosmonautiky a trigonometrie. Kulturní skupina Patria.
- Corral, M. Matematika LibreTexts: Úhly. Obnoveno z: math.libretexts.org.
- Mathmania. Klasifikace a konstrukce úhlů jejich měřením. Obnoveno z: mathemania.com/
- Wentworth, G. Rovinná geometrie. Obnoveno z: gutenberg.org.
- Wikipedia. Konjugované úhly. Obnoveno z: es.wikipedia.org.


Zatím žádné komentáře