Doplňkové úhly, co to jsou, výpočet, příklady, cvičení

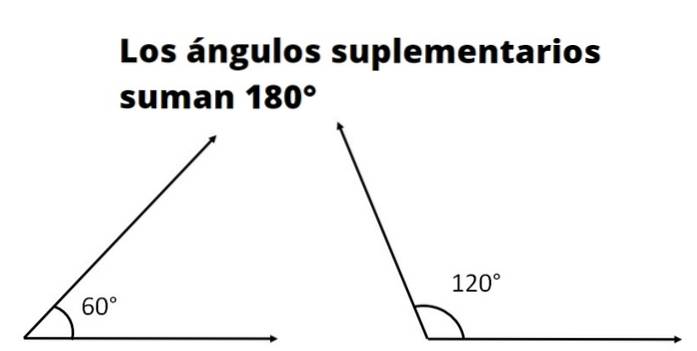
Dva nebo více jsou doplňkové úhly jestliže součet jeho měr odpovídá míře přímého úhlu. Míra přímého úhlu, nazývaného také rovinný úhel, je ve stupních 180 ° a v radiánech π.

Například zjistíme, že tři vnitřní úhly trojúhelníku jsou doplňkové, protože součet jejich měr je 180 °. Na obrázku 1 jsou znázorněny tři úhly. Z výše uvedeného vyplývá, že α a β jsou doplňkové, protože sousedí a jejich součet dotváří přímý úhel.

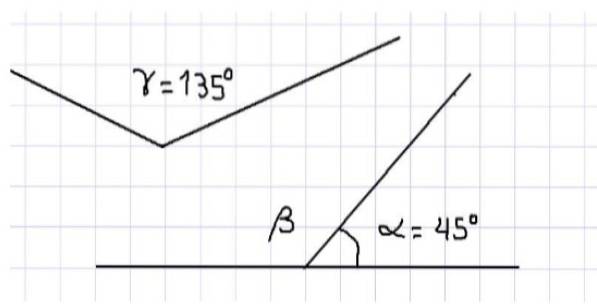
Na stejném obrázku máme také úhly α a γ, které jsou také doplňkové, protože součet jejich měr se rovná míře rovinného úhlu, tj. 180 °. Nelze říci, že úhly β a γ jsou doplňkové, protože jelikož jsou oba úhly tupé, jejich míry jsou větší než 90 °, a proto jejich součet přesahuje 180 °.

Na druhou stranu lze konstatovat, že míra úhlu β se rovná míře úhlu γ, protože pokud je β doplňkové k α a γ je doplňkové k α, pak β = γ = 135 °.

Rejstřík článků

• 1 Příklady
  • 1.1 Příklad A
  • 1.2 Příklad B
  • 1.3 Příklad C
  • 1.4 Příklad D
  • 1.5 Příklad E
  • 1.6 Příklad F
• 2 Cvičení
  • 2.1 - Cvičení I
  • 2.2 - Cvičení II
  • 2.3 - Cvičení III
• 3 Doplňkové úhly ve dvou rovnoběžkách vyříznutých sečnantem
  • 3.1 - Cvičení IV
• 4 Odkazy

Příklady

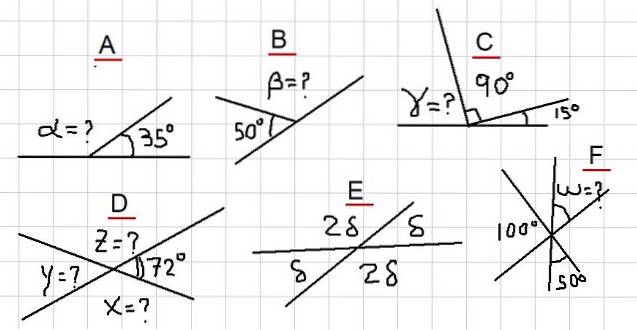
V následujících příkladech je žádáno najít neznámé úhly, které jsou na obrázku 2 označeny otazníky. Od nejjednodušších příkladů po některé jsou trochu komplikovanější, aby čtenář měl být opatrnější.

Příklad A

Na obrázku máme, že sousední úhly α a 35 ° se sčítají s rovinným úhlem. To znamená, že α + 35º = 180º, a proto platí, že: α = 180º- 35º = 145º.

Příklad B

Protože β je doplňkový s úhlem 50 °, vyplývá z toho, že β = 180 ° - 50 ° = 130 °.

Příklad C.

Z obrázku 2C je pozorován následující součet: γ + 90 ° + 15 ° = 180 °. To znamená, že γ je doplňkové s úhlem 105 ° = 90 ° + 15 °. Dospívá se k závěru, že: 

γ = 180 ° - 105 ° = 75 °

Příklad D

Protože X je doplňkový k 72 °, vyplývá z toho, že X = 180 ° - 72 ° = 108 °. Navíc Y je doplňkové s X, takže Y = 180 ° - 108 ° = 72 °.

A nakonec je Z doplňkové s 72 °, proto Z = 180 ° - 72 ° = 108 °.

Příklad E

Úhly δ a 2δ jsou doplňkové, proto δ + 2δ = 180 °. Což znamená, že 3δ = 180º, a to nám zase umožňuje psát: δ = 180º / 3 = 60º.

Příklad F

Pokud nazýváme úhel mezi 100 ° a 50 ° U, pak je U k nim doplňkový, protože je pozorováno, že jejich součet dokončuje rovinný úhel.

Z toho okamžitě vyplývá, že U = 150 °. Vzhledem k tomu, že U je opačným vrcholem k W, pak W = U = 150 °.

Výcvik

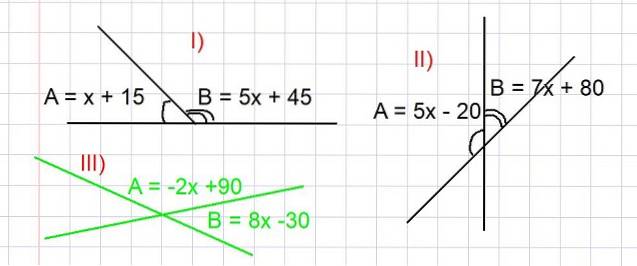
Níže jsou navržena tři cvičení, u všech musí být nalezena hodnota úhlů A a B ve stupních, aby byly splněny vztahy zobrazené na obrázku 3. Při řešení všech je použit koncept doplňkových úhlů..

- Cvičení I

Určete hodnoty úhlů A a B z části I) na obrázku 3.

Řešení

A a B jsou doplňkové, z čehož máme, že A + B = 180 stupňů, pak je výraz A a B nahrazen jako funkce x, jak se zobrazuje na obrázku:

(x + 15) + (5x + 45) = 180

Získá se lineární rovnice prvního řádu. Abychom to vyřešili, jsou termíny seskupeny okamžitě:

6 x + 60 = 180

Vydělením obou členů 6 máme:

x + 10 = 30

A nakonec z toho vyplývá, že x má hodnotu 20º.

Nyní musíme připojit hodnotu x, abychom našli požadované úhly. Úhel A je tedy: A = 20 +15 = 35º.

A pokud jde o jeho část, úhel B je B = 5 * 20 + 45 = 145 °.

- Cvičení II

Najděte hodnoty úhlů A a B z části II) na obrázku 3.

Řešení

Protože A a B jsou doplňkové úhly, máme A + B = 180 stupňů. Dosazením výrazu pro A a B jako funkce x uvedené v části II) na obrázku 3 máme:

(-2x + 90) + (8x - 30) = 180

Opět se získá rovnice prvního stupně, pro kterou je nutné termíny pohodlně seskupit:

6 x + 60 = 180

Vydělením obou členů 6 máme:

x + 10 = 30

Z toho vyplývá, že x má hodnotu 20º.

Jinými slovy, úhel A = -2 * 20 + 90 = 50º. Zatímco úhel B = 8 * 20 - 30 = 130 °.

- Cvičení III

Určete hodnoty úhlů A a B z části III) na obrázku 3 (zeleně).

Řešení

Protože A a B jsou doplňkové úhly, máme A + B = 180 stupňů. Musíme nahradit výraz pro A a B jako funkci x dané na obrázku 3, ze kterého máme:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Vydělením obou členů 12 k řešení hodnoty x máme:

x + 5 = 15

Nakonec se zjistí, že x má hodnotu 10 stupňů.

Nyní přistoupíme k nalezení úhlu A: A = 5 * 10 -20 = 30º. A pro úhel B: B = 7 * 10 + 80 = 150 °

Doplňkové úhly ve dvou rovnoběžkách rozřezaných sečenkou

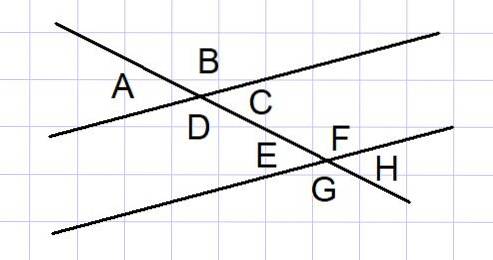
Dvě rovnoběžné čáry řezané sečnantem jsou v některých problémech běžnou geometrickou konstrukcí. Mezi těmito čarami je vytvořeno 8 úhlů, jak je znázorněno na obrázku 4.

Z těchto 8 úhlů jsou některé páry úhlů doplňkové, které uvádíme níže:

1. Vnější úhly A a B a vnější úhly G a H
2. Vnitřní úhly D a C a vnitřní úhly E a F
3. Vnější úhly A a G a vnější úhly B a H
4. Vnitřní úhly D a E a interiéry C a F

Pro úplnost jsou úhly navzájem rovné také pojmenovány:

1. Vnitřní střídání: D = F a C = E
2. Externí střídání: A = H a B = G
3. Odpovídající: A = E a C = H
4. Protiklady vrcholem A = C a E = H
5. Odpovídající: B = F a D = G
6. Protiklady vrcholem B = D a F = G

- Cvičení IV

S odkazem na obrázek 4, který ukazuje úhly mezi dvěma rovnoběžnými přímkami proříznutými sečenkou, určete hodnotu všech úhlů v radiánech s vědomím, že úhel A = π / 6 radiánů.

Řešení

A a B jsou doplňkové vnější úhly, takže B = π - A = π - π / 6 = 5π / 6

A = E = C = H = π / 6

B = F = D = G = 5π / 6

Reference

1. Baldor, J. A. 1973. Geometrie roviny a prostoru. Středoamerický kulturní. 
2. Matematické zákony a vzorce. Systémy pro měření úhlů. Obnoveno z: ingemecanica.com.
3. Wentworth, G. Rovinná geometrie. Obnoveno z: gutenberg.org.
4. Wikipedia. Doplňkové úhly. Obnoveno z: es.wikipedia.com
5. Wikipedia. Dopravník. Obnoveno z: es.wikipedia.com
6. Zapata F. Goniómetro: historie, díly, provoz. Obnoveno z: lifeder.com