Vlastnosti imaginárních čísel, aplikace, příklady

The imaginární čísla jsou ti, kteří dávají řešení rovnice, ve které se neznámé, na druhou, rovná zápornému reálnému číslu. Imaginární jednotka je i = √ (-1).

V rovnici: z^dva= - a, z je imaginární číslo, které je vyjádřeno takto:

 z = √ (-a) = i√ (a)

Bytost na kladné reálné číslo. Ano a = 1, pak z = i, kde i je imaginární jednotka.

Čisté imaginární číslo z je obecně vždy vyjádřeno ve formě: 

z = y⋅i

Kde Y je skutečné číslo e i je imaginární jednotka.

Stejně jako reálná čísla jsou znázorněna na řádku, který se nazývá opravdu rovně, analogickým způsobem jsou imaginární čísla znázorněna na imaginární čára.

The imaginární čára je vždy ortogonální (tvar 90 °) k opravdu rovně a dvě čáry definují kartézskou rovinu zvanou složité letadlo.

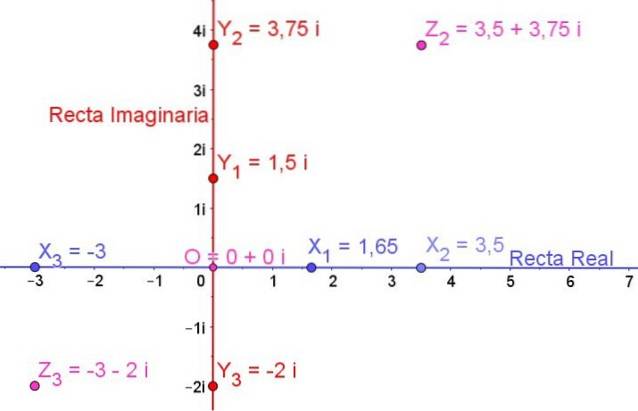
Na obrázku 1 je zobrazena komplexní rovina a na ní jsou znázorněna některá reálná čísla, některá imaginární čísla a také některá komplexní čísla:

X₁, X_dva, X₃ jsou to skutečná čísla

Y₁, Y_dva, Y₃ jsou to imaginární čísla

Z_dva a Z.₃ jsou to komplexní čísla

Číslo O je skutečná nula a je to také imaginární nula, takže počátek O je komplexní nula vyjádřená:

0 + 0i 

Rejstřík článků

• 1 Vlastnosti
  • 1.1 Sčítání a odčítání imaginárního
  • 1.2 Produkt imaginářů
  • 1.3 Produkt reálného čísla jiným imaginárním
  • 1.4 Posílení imaginárního
  • 1.5 Součet reálného čísla a imaginárního čísla
• 2 Aplikace
• 3 Cvičení s imaginárními čísly
  • 3.1 - Cvičení 1
  • 3.2 - Cvičení 2
  • 3.3 - Cvičení 3
  • 3.4 - Cvičení 4
  • 3.5 - Cvičení 5
  • 3.6 - Cvičení 6
• 4 Odkazy

Vlastnosti

Množina imaginárních čísel je označena:

I = …, -3i,…, -2i,…., - i,…., 0i,…., I,…., 2i,…., 3i,…

Na této numerické sadě můžete definovat některé operace. Ne vždy se z těchto operací získá imaginární číslo, pojďme se na ně podívat trochu podrobněji:

Sčítání a odčítání imaginárního

Imaginární čísla lze sčítat a odečítat od sebe, což vede k novému imaginárnímu číslu. Například:

 3i + 2i = 5i

4i - 7i = -3i

Produkt imaginárního

Když vznikne součin jednoho imaginárního čísla s jiným, výsledkem je reálné číslo. Pojďme to zkontrolovat pomocí následující operace:

2i x 3i = 6 x i^dva = 6 x (√ (-1))^dva = 6 x (-1) = -6.

A jak vidíme, -6 je reálné číslo, i když bylo získáno vynásobením dvou čistých imaginárních čísel.

Produkt reálného čísla jiným imaginárním

Pokud je reálné číslo vynásobeno i, výsledkem bude imaginární číslo, které odpovídá otočení o 90 stupňů proti směru hodinových ručiček..

A je to tak, že i^dva odpovídá dvěma po sobě jdoucím rotacím o 90 stupňů, což odpovídá vynásobení -1, tj. i^dva = -1. Je to vidět na následujícím diagramu:

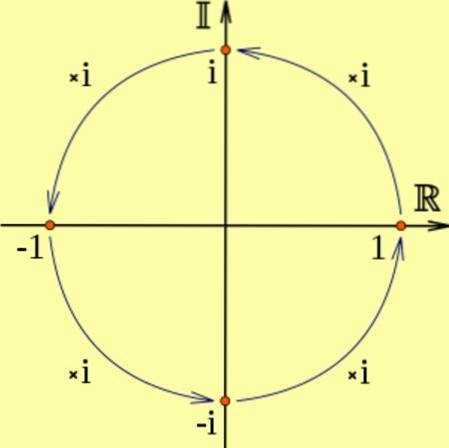
Například:

-3 x 5i = -15i

-3 x i = -3i.

Posílení imaginárního

Můžete definovat potenciaci imaginárního čísla na celočíselný exponent:

i¹ = i

i^dva = i x i = √ (-1) x √ (-1) = -1

i³ = i x i^dva = -i

i⁴ = i^dva x i^dva = -1 x -1 = 1

i⁵ = i x i⁴ = i

Obecně musíte iⁿ = i ^ (n mod 4), kde mod je zbytek rozdělení mezi n Y 4.

Negativní celočíselné potenciace lze také provést:

i^-1 = 1 / i¹ = i / (i x i¹) = i / (i^dva) = i / (-1) = -i

i-^dva = 1 / i^dva = 1 / (-1) = -1

i-³= 1 / i³ = 1 / (- i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Obecně platí, že imaginární číslo b⋅i zvýšené na mocninu n je:

(b⋅i) iⁿ = bⁿ iⁿ = bⁿ i ^ (n mod 4)

Některé příklady jsou následující:

(5 i)¹² = 5¹² i¹² = 5¹² i⁰ = 5¹² x 1 = 244140625

(5 i)^jedenáct = 5^jedenáct i^jedenáct = 5^jedenáct i³ = 5^jedenáct x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ i¹⁰ = 2¹⁰ i^dva = 1024 x (-1) = -1024

Součet reálného čísla a imaginárního čísla

Když přidáte skutečné číslo s imaginárním, výsledek není ani reálný, ani imaginární, jedná se o nový typ čísla s názvem komplexní číslo.

Například pokud X = 3,5 a Y = 3,75i, pak výsledkem je komplexní číslo:

Z = X + Y = 3,5 + 3,75 i

Všimněte si, že v součtu nelze skutečnou a imaginární část seskupit, takže komplexní číslo bude mít vždy skutečnou část a imaginární část..

Tato operace rozšiřuje množinu reálných čísel na nejširší z komplexních čísel.

Aplikace

Název imaginárních čísel navrhl francouzský matematik René Descartes (1596-1650) jako výsměch nebo nesouhlas s návrhem stejného, ​​který podal italský matematik století Raffaelle Bombelli.

Jiní velcí matematici, jako Euler a Leibniz, podporovali Descartese v této neshodě a nazývali imaginární čísla čísla obojživelníků, které byly rozpolceny mezi bytím a ničím.

Název imaginárních čísel zůstává dodnes, ale jejich existence a důležitost je velmi reálná a hmatatelná, protože se přirozeně objevují v mnoha oblastech fyziky, například:

-Teorie relativity.

-V elektromagnetismu.

-Kvantová mechanika.

Cvičení s imaginárními čísly

- Cvičení 1

Najděte řešení následující rovnice:

z^dva + 16 = 0

Řešení

z^dva = -16

Když vezmeme druhou odmocninu u obou členů, máme:

√ (z^dva ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Jinými slovy, řešení původní rovnice jsou:

z = + 4i nebo z = -4i.

- Cvičení 2

Najděte výsledek zvýšení imaginární jednotky na sílu 5 minus odečtení imaginární jednotky zvýšené na sílu -5.

Řešení

i⁵ - i-⁵ = i⁵ - 1 / i⁵ = i - 1 / i = i - (i) / (i x i) = i - i / (- 1) = i + i = 2i

- Cvičení 3

Najděte výsledek následující operace:

(3i)³ + 9i 

Řešení

3³ i³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Cvičení 4

Najděte řešení následující kvadratické rovnice:

(-2x)^dva + 2 = 0

Řešení

Rovnice je uspořádána takto:

(-2x)^dva = -2

Pak se vezme druhá odmocnina obou členů

√ ((- 2x)^dva) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Pak vyřešíme pro x, abychom konečně získali:

x = ± √2 / 2 i

To znamená, že existují dvě možná řešení:

x = (√2 / 2) i

Nebo tento jiný:

x = - (√2 / 2) i

- Cvičení 5

Najděte hodnotu Z definovanou:

Z = √ (-9) √ (-4) + 7

Řešení

Víme, že druhá odmocnina záporného reálného čísla je imaginární číslo, například √ (-9) se rovná √ (9) x √ (-1) = 3i.

Na druhou stranu, √ (-4) se rovná √ (4) x √ (-1) = 2i.

Takže původní rovnici lze nahradit:

3i x 2i - 7 = 6 i^dva - 7 = 6 (-1) - 7 = -6 - 7 = -13

- Cvičení 6

Najděte hodnotu Z vyplývající z následujícího dělení dvou komplexních čísel:

Z = (9 - tj^dva) / (3 + i)

Řešení

Čitatel výrazu lze faktorovat pomocí následující vlastnosti:

Rozdíl čtverců je součinem součtu a rozdílu binomiků bez čtverců.

Pak:

Z = [(3 - i) (3 + i)] / (3 + i)

Výsledný výraz se poté zjednoduší a odejde

Z = (3 - i)

Reference

1. Earl, R. Složitá čísla. Obnoveno z: maths.ox.ac.uk.
2. Figuera, J. 2000. Matematika 1.. Diverzifikovaný. Vydání CO-BO.
3. Hoffmann, J. 2005. Výběr témat matematiky. Publikace Monfort.
4. Jiménez, R. 2008. Algebra. Hala Prentice.
5. Wikipedia. Imaginární číslo. Obnoveno z: en.wikipedia.org