The iracionální čísla jsou ti, jejichž desítkový výraz má nekonečné číslice bez opakujícího se vzoru, proto je nelze získat vytvořením kvocientu mezi libovolnými dvěma celými čísly.
Mezi nejznámější iracionální čísla patří:
Mezi nimi je bezpochyby nejznámější π (pi), ale je jich mnohem více. Všichni patří do množiny reálných čísel, což je číselná množina, která seskupuje racionální a iracionální čísla..
Elipsa na obrázku 1 naznačuje, že desetinná místa pokračují neurčitě, co se stane, je, že prostor běžných kalkulaček umožňuje zobrazit pouze několik.
Podíváme-li se pečlivě, kdykoli uděláme kvocient mezi dvěma celými čísly, získáme desetinnou čárku s omezenými čísly, nebo pokud ne, s nekonečnými čísly, ve kterých se opakuje jedna nebo více. To se u iracionálních čísel neděje..
Rejstřík článků
Velký starověký matematik Pythagoras, narozený v roce 582 př. N.l. v Samosu v Řecku, založil Pythagorovu myšlenkovou školu a objevil slavnou větu, která nese jeho jméno. Máme to tady dole vlevo (možná to Babylóňané věděli už dávno předtím).
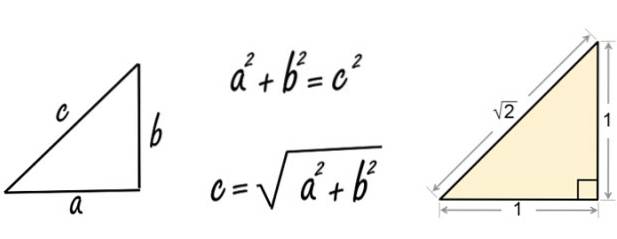
Když tedy Pythagoras (nebo pravděpodobně jeho žák) použil teorém na pravý trojúhelník se stranami rovnými 1, našel iracionální číslo √2.
Udělal to takto:
c = √1dva + 1dva = √1 + 1 = √2
A okamžitě si uvědomil, že toto nové číslo nepochází z kvocientu mezi dvěma dalšími přirozenými čísly, která byla v té době známá.
Proto to nazval iracionální, a objev způsobil mezi Pythagorovci velkou úzkost a zmatek.
-Sada všech iracionálních čísel je označena písmenem I a někdy jako Q * nebo QC. Spojení mezi iracionálními čísly I nebo Q * a racionálními čísly Q vede k množině reálných čísel R.
-S iracionálními čísly lze provádět známé aritmetické operace: sčítání, odčítání, násobení, dělení, zmocnění a další.
-Dělení 0 také není definováno mezi iracionálními čísly.
-Součet a součin mezi iracionálními čísly nemusí nutně znamenat další iracionální číslo. Například:
√2 x √8 = √16 = 4
A 4 není iracionální číslo.
-Součet racionálního čísla plus iracionálního čísla však vede k iracionálnímu. Takto:
1 + √2 = 2,41421356237…
-Součin racionálního čísla jiného než 0 iracionálním číslem je také iracionální. Podívejme se na tento příklad:
2 x √2 = 2,828427125…
-Inverze iracionální má za následek další iracionální číslo. Zkusme některé:
1 / √2 = 0,707106781…
1 / √3 = 0,577350269…
Tato čísla jsou zajímavá, protože jsou také hodnotami některých trigonometrických poměrů známých úhlů. Většina trigonometrických poměrů jsou iracionální čísla, ale existují výjimky, například sin 30º = 0,5 = ½, což je racionální.
-Kromě toho jsou splněny komutativní a asociativní vlastnosti. Pokud jsou a a b dvě iracionální čísla, znamená to, že:
a + b = b + a.
A pokud c je jiné iracionální číslo, pak:
(a + b) + c = a + (b + c).
-Distribuční vlastnost násobení s ohledem na sčítání je další známá vlastnost, která platí i pro iracionální čísla. V tomto případě:
a. (b + c) = a.b + a.c.
-Iracionální a má svůj opak: -a. Když se sečtou, výsledkem je 0:
a + (- a) = 0
-Mezi dvěma různými racionálními je alespoň jedno iracionální číslo.
Skutečná čára je vodorovná čára, kde jsou umístěna reálná čísla, jejichž iracionály jsou důležitou součástí.
K nalezení iracionálního čísla na reálné linii v geometrické podobě můžeme použít Pythagorovu větu, pravítko a kompas.
Jako příklad najdeme √5 na reálné přímce, pro kterou nakreslíme pravý trojúhelník se stranami x = 2 Y y = 1, jak ukazuje obrázek:
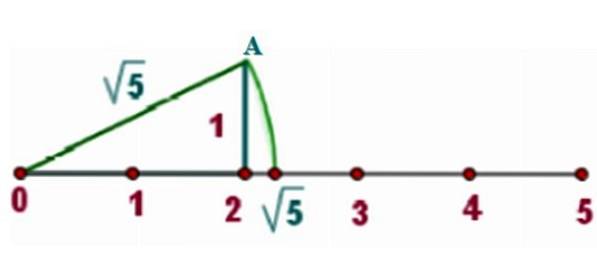
Podle Pythagorovy věty je přepona takového trojúhelníku:
c = √2dva + 1dva = √4 + 1 = √5
Nyní je kompas umístěn s bodem na 0, kde je také jeden z vrcholů pravého trojúhelníku. Bod tužky kompasu by měl být na vrcholu A.
Je nakreslen oblouk obvodu, který se prořízne ke skutečné linii. Protože vzdálenost mezi středem obvodu a jakýmkoli bodem na něm je poloměr, který se rovná √5, je průsečík také daleko √ 5 od středu.
Z grafu je vidět, že √5 je mezi 2 a 2,5. Kalkulačka nám dává přibližnou hodnotu:
√5 = 2,236068
A tak vytvořením trojúhelníku s příslušnými stranami lze lokalizovat další iracionální, například √7 a další.
Iracionální čísla jsou rozdělena do dvou skupin:
-Algebraický
-Transcendentní nebo transcendentální
Algebraická čísla, která mohou nebo nemusí být iracionální, jsou řešením polynomiálních rovnic, jejichž obecná forma je:
nan Xn + nan-1Xn-1 + nan-2Xn-2 +…. + a1x + anebo = 0
Příkladem polynomiální rovnice je kvadratická rovnice, jako je tato:
X3 - 2x = 0
Je snadné ukázat, že iracionální číslo √2 je jedním z řešení této rovnice.
Na druhou stranu, transcendentní čísla, i když jsou iracionální, nikdy nevzniknou jako řešení polynomiální rovnice.
Transcendentní čísla, která se v aplikované matematice vyskytují nejčastěji, jsou π, kvůli jeho vztahu s obvodem a číslem e, neboli Eulerovo číslo, které je základem přirozených logaritmů..
Šedý čtverec se umístí na černý čtverec v poloze uvedené na obrázku. Je známo, že povrch černého čtverce je 64 cmdva. Kolik jsou délky obou čtverců?
Plocha čtverce se stranou L je:
A = Ldva
Protože černý čtverec je 64 cmdva plochy, její strana by měla být 8 cm.
Toto měření je stejné jako úhlopříčka šedého čtverce. Použitím Pythagorovy věty na tuto úhlopříčku a zapamatováním, že strany čtverce měří stejně, budeme mít:
8dva = LGdva + LGdva
Kde LG je strana šedého čtverce.
Proto: 2LGdva = 8dva
Použití druhé odmocniny na obě strany rovnosti:
LG = (8 / √2) cm
Zatím žádné komentáře