
Historie reálných čísel, příklady, vlastnosti, operace

The reálná čísla tvoří číselnou množinu, která zahrnuje přirozená čísla, celá čísla, racionální a iracionální. Jsou označeny symbolem ℝ nebo jednoduše R a rozsah, který mají ve vědě, strojírenství a ekonomii, je takový, že když se mluví o „čísle“, je téměř považováno za samozřejmé, že jde o skutečné číslo.
Skutečná čísla se používají od starověku, i když jim toto jméno nebylo dáno. Již od doby, kdy Pythagoras vyvinul svou slavnou větu, vznikla čísla, která nebylo možné získat jako kvocienty přirozených čísel nebo celých čísel.
Příklady čísel jsou √2, √3 a π. Tato čísla se nazývají iracionální, na rozdíl od racionálních čísel, která pocházejí z celočíselných poměrů. Proto byla nutná numerická množina, která by zahrnovala obě třídy čísel..
Termín „skutečné číslo“ vytvořil skvělý matematik René Descartes (1596-1650), aby rozlišoval mezi dvěma druhy kořenů, které mohou vzniknout při řešení polynomické rovnice.
Některé z těchto kořenů mohou být dokonce kořeny záporných čísel, Descartes tyto „imaginární čísla“ nazval a ty, které nebyly, byly skutečnými čísly.
Označení přetrvávalo v průběhu času a vedlo ke vzniku dvou velkých číselných sad: reálných čísel a komplexních čísel, větší množiny, která zahrnuje reálná čísla, imaginárních čísel a těch, které jsou částečně reálné a částečně imaginární..
Vývoj reálných čísel pokračoval ve svém průběhu, dokud v roce 1872 matematik Richard Dedekind (1831-1936) formálně definoval množinu reálných čísel prostřednictvím tzv. řezy podle Dedekind. Syntéza jeho práce byla publikována v článku, který viděl světlo téhož roku.
Rejstřík článků
- 1 Příklady reálných čísel
- 1.1 Reprezentace reálných čísel na reálné linii
- 2 Vlastnosti reálných čísel
- 3 Operace se skutečnými čísly
- 4 Aplikace
- 5 Cvičení vyřešeno
- 5.1 Cvičení 1
- 6 Reference
Příklady reálných čísel
Tabulka níže ukazuje příklady reálných čísel. Tato sada má jako podmnožiny přirozená čísla, celá čísla, racionální a iracionální. Libovolný počet těchto sad je sám o sobě reálným číslem.
Proto 0, negativy, pozitivy, zlomky a desetinná místa jsou reálná čísla.

Reprezentace reálných čísel na reálné linii
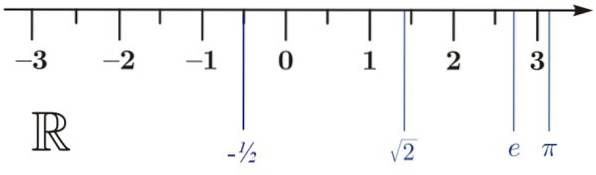
Reálná čísla lze vyjádřit na reálné linii R, jak ukazuje obrázek. Není nutné, aby 0 byla vždy přítomna, nicméně je vhodné vědět, že nalevo jsou záporné reálné a napravo kladné. Proto je vynikajícím referenčním bodem.
Na reálné linii se vezme stupnice, ve které se nacházejí celá čísla:… 3, -2, -1, 1, 2, 3…. Šipka označuje, že čára sahá do nekonečna. Ale to není vše, v každém uvažovaném intervalu také vždy najdeme nekonečná reálná čísla.
Skutečná čísla jsou uvedena v pořadí. Pro začátek je zde pořadí celých čísel, ve kterých jsou pozitivy vždy větší než 0, zatímco negativy jsou menší..
Toto pořadí je udržováno v reálných číslech. Jako příklad jsou uvedeny následující nerovnosti:
a) -1/2 < √2
b) e < π
c) π> -1/2
Vlastnosti reálných čísel
-Skutečná čísla zahrnují přirozená čísla, celá čísla, racionální čísla a iracionální čísla..
-Komutativní vlastnost sčítání je splněna: pořadí sčítání nemění součet. Pokud a a b jsou dvě reálná čísla, vždy platí, že:
a + b = b + a
-0 je neutrální prvek součtu: a + 0 = a
-Pro součet je asociativní vlastnost splněna. Pokud a, bac jsou reálná čísla: (a + b) + c = a + (b + c).
-Opakem reálného čísla je -a.
-Odečtení je definováno jako součet opaku: a - b = a + (-b).
-Komutativní vlastnost produktu je splněna: pořadí faktorů produkt nemění: a.b = b.a
-V produktu se také použije asociativní vlastnost: (a.b) .c = a. (B.c)
-1 je neutrální prvek násobení: a.1 = a
-Distribuční vlastnost násobení s ohledem na sčítání je platná: a. (b + c) = a.b + a.c
-Dělení 0 není definováno.
-Jakékoli reálné číslo a, s výjimkou 0, má multiplikativní inverzní hodnotu-1 takové, že a.a.-1 = 1.
-Pokud a je reálné číslo: a0 = 1 a1 = a.
-Absolutní hodnota nebo modul reálného čísla je vzdálenost mezi uvedeným číslem a 0.
Operace se skutečnými čísly
Se skutečnými čísly můžete provádět operace, které se provádějí s jinými numerickými množinami, včetně sčítání, odčítání, násobení, dělení, zmocnění, radikace, logaritmy a další.
Jako vždy není definováno dělení 0, nejde ani o záporné logaritmy čísel, ani o 0, i když je pravda, že log 1 = 0 a že logaritmy čísel mezi 0 a 1 jsou záporné.
Aplikace
Aplikace reálných čísel na všechny druhy situací jsou velmi rozmanité. Reálná čísla se objevují jako odpovědi na mnoho problémů v exaktní vědě, počítačové vědě, strojírenství, ekonomii a společenských vědách..
Všechny druhy veličin a veličin, jako jsou vzdálenosti, časy, síly, intenzita zvuku, peníze a mnoho dalších, mají svůj výraz v reálných číslech.
Přenos telefonních signálů, obrazu a zvuku videa, teploty klimatizace, topení nebo ledničky lze ovládat digitálně, což znamená přeměnu fyzických veličin na číselné sekvence.
Totéž se děje při provádění bankovních transakcí přes internet nebo při konzultaci okamžitých zpráv. Skutečná čísla jsou všude.
Cvičení vyřešeno
Uvidíme pomocí cvičení, jak tato čísla fungují v běžných situacích, s nimiž se denně setkáváme..
Cvičení 1
Pošta přijímá pouze balíčky, u nichž délka plus měření obvodu nepřesahuje 108 palců. Aby byl zobrazený balíček přijat, musí být splněno, že:
L + 2 (x + y) ≤ 108
a) Provede balíček, který měří 6 palců široký, 8 palců vysoký a 5 stop dlouhý??
b) A co ten, který měří 2 x 2 x 4 stopy3?
c) Jaká je nejvyšší přijatelná výška pro balíček, jehož základna je čtvercová a měří 9 x 9 palcůdva?
Odpovědět
L = 5 stop = 60 palců
x = 6 palců
y = 8 palců
Operace k řešení je:
L + 2 (x + y) = 60 + 2 (6 + 8) palců = 60 + 2 x 14 palců = 60 + 28 palců = 88 palců
Balíček je přijat.
Odpověď b
Rozměry tohoto paketu jsou menší než paketu a), takže se oběma podaří projít.
Odpověď c
V tomto balíčku:
x = L = 9 palců
Musí být splněno, že:
9+ 2 (9 + y) ≤ 108
27 + 2r ≤ 108
2 roky ≤ 81
a ≤ 40,5 palce
Reference
- Carena, M. 2019. Pre-University Matematická příručka. Národní univerzita v Litoralu.
- Diego, A. Reálná čísla a jejich vlastnosti. Obnoveno z: matematica.uns.edu.ar.
- Figuera, J. 2000. Matematika 9.. Školní známka. Vydání CO-BO.
- Jiménez, R. 2008. Algebra. Hala Prentice.
- Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Edice. Cengage Learning.


Zatím žádné komentáře