
Papomudas Jak je řešit a cvičit
The papomudas je postup pro řešení algebraických výrazů. Jeho akronymy označují pořadí priorit operací: závorky, mocniny, násobení, dělení, sčítání a odčítání. Pomocí tohoto slova si snadno zapamatujete pořadí, ve kterém musíte vyřešit výraz složený z několika operací.
Obecně lze v numerických výrazech najít několik aritmetických operací najednou, například sčítání, odčítání, násobení a dělení, což mohou být také zlomky, mocniny a kořeny. K jejich vyřešení je nutné dodržet postup, který zaručuje správnost výsledků..

Aritmetický výraz, který je tvořen kombinací těchto operací, musí být vyřešen podle priority pořadí, známé také jako hierarchie operací, zavedené dávno v univerzálních konvencích. Všichni lidé tak mohou postupovat stejným způsobem a dosáhnout stejného výsledku.
Rejstřík článků
- 1 Funkce
- 2 Jak je vyřešit?
- 3 Aplikace
- 3.1 Výrazy obsahující sčítání a odčítání
- 3.2 Výrazy obsahující sčítání, odčítání a násobení
- 3.3 Výrazy obsahující sčítání, odčítání, násobení a dělení
- 3.4 Výrazy obsahující sčítání, odčítání, násobení, dělení a mocniny
- 3.5 Výrazy, které používají seskupovací symboly
- 4 cvičení
- 4.1 První cvičení
- 4.2 Druhé cvičení
- 4.3 Třetí cvičení
- 5 Reference
Vlastnosti
Papomudas je standardní postup, který stanoví pořadí, které je třeba dodržet při řešení výrazu, který se skládá z kombinace operací, jako je sčítání, odčítání, násobení a dělení..
Tímto postupem se stanoví pořadí priority operace ve vztahu k ostatním v okamžiku, kdy budou výsledkem; to znamená, že každá operace má posun nebo hierarchickou úroveň, kterou je třeba vyřešit.
Pořadí, ve kterém musí být vyřešeny různé operace výrazu, je dáno každou zkratkou slova papomudas. Musíte tedy:
1- Pa: závorky, závorky nebo závorky.
2 - Po: pravomoci a kořeny.
3 - Mu: množení.
4- D: divize.
5- A: doplňky nebo doplňky.
6- S: odčítání nebo odčítání.
Tento postup se také v angličtině nazývá PEMDAS; toto slovo si snadno zapamatujete, je spojeno s frází: „Pčíst Axcuse MY Ducho NAne Sspojenec”, Kde každé počáteční písmeno odpovídá aritmetické operaci, stejně jako papomudy.
Jak je vyřešit?
Na základě hierarchie vytvořené papomudami k řešení operací výrazu je nutné splnit následující pořadí:
- Všechny operace v rámci seskupovacích symbolů, jako jsou závorky, složené závorky, hranaté závorky a zlomkové čáry, musí být nejprve vyřešeny. Pokud jsou v ostatních symboly seskupování, musíte začít počítat zevnitř ven.
Tyto symboly se používají ke změně pořadí, ve kterém jsou operace řešeny, protože to, co je v nich, musí být vždy vyřešeno jako první..
- Poté jsou vyřešeny pravomoci a kořeny.
- Na třetím místě jsou řešeny násobení a dělení. Mají stejné pořadí priorit; proto, když jsou tyto dvě operace nalezeny ve výrazu, musí být vyřešena ta, která se objeví jako první, čtení výrazu zleva doprava.
- Na posledním místě jsou vyřešeny sčítání a odčítání, která mají také stejné pořadí priority, a proto je vyřešen ten, který se ve výrazu zobrazí jako první, čtení zleva doprava.
- Při čtení zleva doprava by operace nikdy neměly být smíšené, mělo by se vždy dodržovat pořadí priority nebo hierarchie stanovené papomudami..
Je důležité si uvědomit, že výsledek každé operace musí být umístěn ve stejném pořadí ve vztahu k ostatním a všechny mezikroky musí být odděleny znaménkem, dokud není dosaženo konečného výsledku..
Aplikace
Procedura papomudas se používá, když máte kombinaci různých operací. S ohledem na to, jak jsou vyřešeny, to lze použít v:
Výrazy obsahující sčítání a odčítání
Je to jedna z nejjednodušších operací, protože obě mají stejné pořadí priorit, a to takovým způsobem, že musí být vyřešeno ve výrazu zleva doprava; například:
22-15 + 8 +6 = 21.
Výrazy obsahující sčítání, odčítání a násobení
V tomto případě je operací s nejvyšší prioritou násobení, poté se vyřeší sčítání a odčítání (podle toho, co je ve výrazu první). Například:
6 * 4 - 10 + 8 * 6 - 16 + 10 * 6
= 24-10 + 48-16 + 60
= 106.
Výrazy obsahující sčítání, odčítání, násobení a dělení
V tomto případě máte kombinaci všech operací. Začnete tím, že vyřešíte násobení a dělení, které mají vyšší prioritu, pak sčítání a odčítání. Při čtení výrazu zleva doprava je řešen podle jeho hierarchie a polohy ve výrazu; například:
7 + 10 * 13 - 8 + 40 ÷ 2
= 7 + 130 - 8 + 20
= 149.
Výrazy obsahující sčítání, odčítání, násobení, dělení a mocniny
V tomto případě je jedno z čísel povýšeno na mocninu, kterou je třeba nejprve vyřešit v rámci úrovně priority, poté vyřešit násobení a dělení a nakonec sčítání a odčítání:
4 + 4dva * 12 - 5 + 90 ÷ 3
= 4 + 16 * 12 - 5 + 90 ÷ 3
= 4 + 192 - 5 + 30
= 221.
Stejně jako mocnosti mají kořeny také druhý stupeň priority; Proto ve výrazech, které je obsahují, je třeba nejprve vyřešit násobení, dělení, sčítání a odčítání:
5 * 8 + 20 ÷ √16
= 5 * 8 + 20 ÷ 4
= 40 + 5
= 45.
Výrazy, které používají seskupovací symboly
Když se použijí znaky jako závorky, závorky, závorky a zlomky, vyřeší se nejdříve to, co je uvnitř, bez ohledu na pořadí priorit operací, které obsahuje, ve vztahu k těm vně, jako by to bude samostatný výraz :
14 ÷ 2 - (8 - 5)
= 14 ÷ 2 - 3
= 7 - 3
= 4.
Pokud v něm existuje několik operací, musí být vyřešeny v hierarchickém pořadí. Pak jsou vyřešeny další operace, které tvoří výraz; například:
2 + 9 * (5 + 23 - 24 ÷ 6) - 1
= 2 + 9 * (5 + 8 - 4) - 1
= 2 + 9 * 9 - 1
= 2 + 81 - 1
= 82.
Některé výrazy používají seskupovací symboly v jiných, například když je nutné změnit znaménko operace. V těchto případech musíte začít řešením zevnitř ven; to znamená zjednodušení seskupovacích symbolů, které jsou ve středu výrazu.
Obecně platí, že pořadí řešení operací obsažených v těchto symbolech je: nejprve vyřešte to, co je uvnitř závorek (), potom závorky [] a poslední závorky .
90 - 3*[12 + (5*4) - (4*dva)]
= 90 - 3* [12 + 20 - 8]
= 90 - 3 * 24
= 90 - 72
= 18.
Výcvik
První cvičení
Najděte hodnotu následujícího výrazu:
dvacetdva + √225 - 155 + 130.
Řešení
Při použití papomud je třeba nejprve vyřešit pravomoci a kořeny a poté sčítání a odčítání. V tomto případě patří první dvě operace do stejného pořadí, takže je vyřešena ta, která je první, počínaje zleva doprava:
dvacetdva + √225 - 155 + 130
= 400 + 15 - 155 + 130.
Pak přidáte a odečtete, počínaje také zleva:
400 + 15 - 155 + 130
= 390.
Druhé cvičení
Najděte hodnotu následujícího výrazu:
[- (63 - 36) ÷ (8 * 6 ÷ 16)].
Řešení
Začíná to řešením operací, které jsou uvnitř závorek, podle hierarchického pořadí, které mají podle papomud.
Nejprve jsou vyřešeny pravomoci první závorky, poté jsou vyřešeny operace druhé závorky. Protože patří do stejného řádu, je vyřešena první operace výrazu:
[- (63 - 36) ÷ (8 * 6 ÷ 16)]
= [- (216 - 729) ÷ (8 * 6 ÷ 16)]
= [- (216 - 729) ÷ (48 ÷ 16)]
= [- (-513) ÷ (3)].
Protože operace v závorkách již byly vyřešeny, nyní pokračujeme s rozdělením, které má vyšší hierarchii než odčítání:
[- (-513) ÷ (3)] = [- (-171)].
Nakonec závorka, která odděluje znaménko mínus (-) od výsledku, který je v tomto případě záporný, naznačuje, že tyto znaménka musí být vynásobena. Výsledek výrazu je tedy:
[- (-171)] = 171.
Třetí cvičení
Najděte hodnotu následujícího výrazu:

Řešení
Začnete řešením zlomků, které jsou uvnitř závorek:
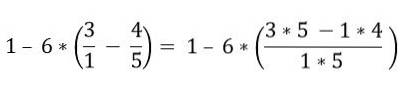
Uvnitř závorek je několik operací. Nejprve se vyřeší násobení a poté odčítání; V tomto případě je zlomková lišta považována za symbol seskupení a nikoli za rozdělení, z tohoto důvodu musí být vyřešeny operace horní a dolní části:
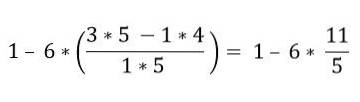
V hierarchickém pořadí musí být násobení vyřešeno:
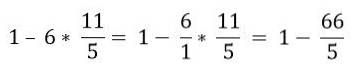
Nakonec je vyřešeno odčítání:
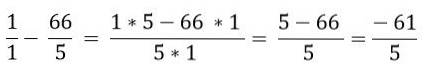
Reference
- Aguirre, H. M. (2012). Finanční matematika. Cengage Learning.
- Aponte, G. (1998). Základy základní matematiky. Pearson Education.
- Cabanne, N. (2007). Didaktika matematiky.
- Carolina Espinosa, C. C. (2012). Zdroje v učebních operacích.
- Huffstetler, K. (2016). Příběh řádu operací: Pemdas. Vytvořit prostor nezávislý .
- Madore, B. (2009). GRE Matematický sešit. Barronova vzdělávací série,.
- Molina, F. A. (s.f.). Azarquiel Project, Mathematics: First cycle. Skupina Azarquiel.



Zatím žádné komentáře