
Vzorec hydrostatického tlaku, výpočet, příklady, cvičení

The hydrostatický tlak je ten, který vyvíjí tekutinu ve statické rovnováze v kterémkoli bodě svého vnitřku, ať už je to povrch v ní ponořený, stěny nádoby nebo část tekutiny, která tvoří část celkové hmotnosti.
Způsob, jakým tekutiny vyvíjejí tlak, se liší od pevných látek. Vyvíjejí tlak směrem dolů, ale kapalina nebo plyn tak činí ve všech směrech.

Pokud jde o kapalinu, tlak se zvyšuje s hloubkou, jak je známo ze zkušeností při ponoření do vody, ve které je zvýšení tlaku pociťováno v uších. Tento tlak pochází z hmotnosti tekutiny a neustálého pohybu částic, které ji tvoří, které nepřetržitě narážejí na povrch těla ponořeného do tekutiny..
Pokud předpokládáme nestlačitelnou kapalinu - což je pravda ve velké většině aplikací - její hustota zůstává konstantní a v tomto případě tlak lineárně závisí na hloubce..
Rejstřík článků
- 1 vzorec
- 2 Příklady hydrostatického tlaku
- 2.1 Konstrukce, kde je relevantní hydrostatický tlak
- 3 cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Vzorec
Hydrostatický tlak se vypočítá pomocí následujícího výrazu:
P = Pbankomat + ρ · g · h
Kde:
-P tlak vyvíjený v bodě
-Pbankomat je tlak atmosféry na volném povrchu
-ρ je hustota kapaliny
-g je gravitační zrychlení
-h je hloubka, ve které chcete vypočítat hydrostatický tlak
Vzorec zahrnuje účinky atmosféry, ale mnoho tlakoměrů nebo manometrů umisťuje 0 na atmosférický tlak, z tohoto důvodu měří diferenciální tlak nebo relativní tlak, nazývaný také měřicí tlak:
Pm = ρ · g · h
Pokud jde o plyny, velmi snadno se stlačují nebo expandují. Proto je jeho hustota, což je poměr mezi hmotností a objemem, v případě atmosférických plynů obvykle funkcí jiných parametrů, jako je nadmořská výška a teplota..
Tlak vyvíjený plyny se často nazývá aerostatický tlak, termín hydrostatický tlak je vyhrazen pro kapaliny.
Příklady hydrostatického tlaku
Hydrostatický tlak závisí pouze na hloubce, takže tvar nebo plocha dna nádoby nejsou relevantní.
Protože tlak P je definován jako kolmá složka síly F na jednotku plochy A:
P = F / A
Pak může být síla vyvíjená kapalinou na dno nádoby odlišná, ale protože je rozložena na různé nástavce, je tlak, kterým je poměr síla / plocha, stejný pro body ve stejné hloubce..
Zvažte nádoby na obrázku. Tlak je stejný pro všechny červené tečky, které jsou na stejné úrovni, i když nad touto hladinou je ve střední nádobě větší množství tekutiny - širší - než je válcová a tenká trubice zcela vlevo..
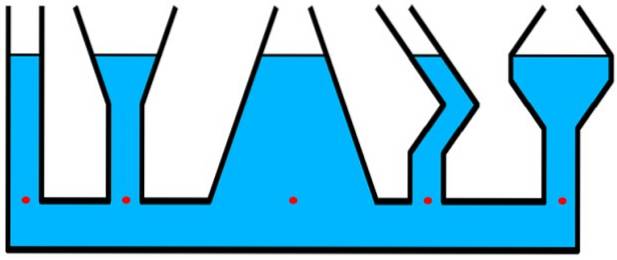
Konstrukce, kde je relevantní hydrostatický tlak
-Stěny přehrady: ačkoli síla je stejná pro všechny body plochého dna, na svislé stěně roste s rostoucí hloubkou, proto jsou opěrné zdi u základny širší než nahoře.
-Na stěnách a na dně bazénu.
-Ve hvězdách, jako je naše Slunce, kde hydrostatický tlak vyvažuje gravitační sílu a udržuje hvězdu v chodu. Když je tato rovnováha narušena, hvězda se zhroutí a podstoupí extrémní změny ve své struktuře..
-Akumulační nádrže na kapaliny, které jsou odolné proti hydrostatickému tlaku. Nejen stěny, ale brány, které usnadňují plnění a odsávání. Pro jeho konstrukci se bere v úvahu, zda je kapalina korozivní, a také tlak a síla, kterou vyvíjí, podle její hustoty.
-Pneumatiky a balónky, které jsou nahuštěny tak, aby odolávaly tlaku kapaliny (plynu nebo kapaliny) bez roztržení.
-Každé ponořené těleso, které zažívá svislý tah směrem vzhůru nebo „odlehčuje“ svou hmotnost díky hydrostatickému tlaku vyvíjenému kapalinou. Toto je známé jako Archimédův princip.
Výcvik
Archimédův princip uvádí, že když je tělo ponořeno, zcela nebo částečně, zažije vzestupnou vertikální sílu, známou jako tah. Velikost tahu se číselně rovná hmotnosti objemu vody vytlačeného objektem..

Nechť ρtekutina hustota kapaliny, Vs ponořený objem, g gravitační zrychlení a B velikost tahu, kterou můžeme vypočítat pomocí následujícího výrazu:
B = ρtekutina .PROTIs .G
- Cvičení 1
Obdélníkový blok o rozměrech 2,0 cm x 2,0 cm x 6,0 cm se vznáší ve sladké vodě s nejdelší svislou osou. Délka bloku, který vyčnívá nad vodu, je 2,0 cm. Vypočítejte hustotu bloku.
Řešení
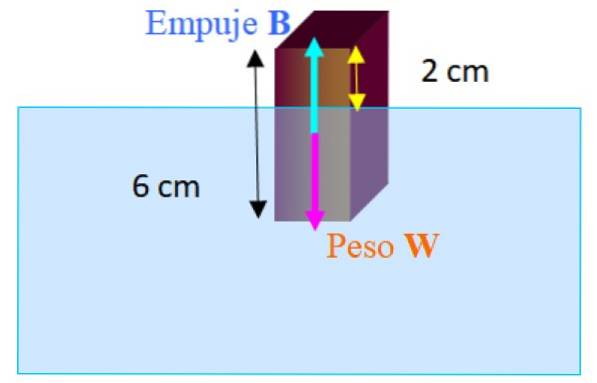
Síly působící na blok jsou váha Ž dolů a vrazit B nahoru. Když se blok vznáší v rovnováze, máme:
∑ FY = B - W = 0
B = W
Velikost hmotnosti W je součinem hmotnosti m bloku a gravitačního zrychlení. Použijeme definici hustoty ρnebo jako podíl mezi hmotou m a objem PROTI bloku:
ρnebo = m / V → m = ρnebo . PROTI
Jeho část je tah:
B = ρtekutina .PROTIs .G
Rovnácí se velikost tahu a velikost hmotnosti:
ρtekutina .PROTIs .g = ρnebo . Např
Gravitace se ruší tím, že je faktorem na obou stranách a hustotu bloku lze vyřešit jako:
ρnebo = ρtekutina . (PROTIs / V)
Hustota vody v jednotkách mezinárodního systému je 1000 kg / m3. Objemy celkem V a ponořené Vs, se počítají pomocí V = šířka x výška x hloubka:
V = 2,0 cm x 2,0 cm x 6,0 cm = 24,0 cm3
PROTIs = 2,0 cm x 2,0 cm x 4,0 cm = 16,0 cm3
Nahrazení hodnot:
ρnebo = ρtekutina . (PROTIs / V) = 1000 kg / m3 . (16/24) = 667 kg / m3
- Cvičení 2
Vypočítejte procento ponořeného objemu kusu ledu plovoucího v mořské vodě při 0 ° C.
Řešení
Led plave na vodě, protože jeho hustota je nižší: 916,8 kg / m3, což znamená, že se při ochlazení rozpíná, na rozdíl od většiny látek, které při zahřívání zvětšují svůj objem.

Je to velmi šťastná okolnost pro život, protože od té doby masy vody zmrznou pouze na povrchu a zůstávají kapalné v hloubce.
Hustota mořské vody je o něco vyšší než hustota sladké vody: 1027 kg / m3. Vypočítáme objemový zlomek Vs / V:
PROTIs / V = ρnebo / ρtekutina = 916,8 kg / m3 / 1027 kg / m3 = 0,8927
To znamená, že přibližně 89% ledu zůstává ponořeno pod vodou. Pouze 11% je viditelné plovoucí na moři.
Reference
- Giambattista, A. 2010. Fyzika. 2. místo Ed. McGraw Hill.
- Knight, R. 2017. Fyzika pro vědce a inženýrství: strategický přístup. Pearson.
- Cimbala, C. 2006. Mechanika tekutin, základy a aplikace. Mc. Graw Hill.
- Hibbeler, R. 2015. Fluid Mechanics. 1. místo Ed. Pearson.
- Mott, R. 2006. Fluid Mechanics. 4. místo. Edice. Pearson Education.
- Streeter, V. 1999. Fluid Mechanics. Mcgraw kopec.



Zatím žádné komentáře