The lisrelativní na je ten, který se měří s ohledem na určitou hodnotu nebo datum, což je obvykle atmosférický tlak na hladině moře (standardní atmosférický tlak). To je vhodné, protože velká část měření tlaku se provádí pod plynnými vrstvami, které tvoří atmosféru a které vyvíjejí vlastní tlak..
Místo toho se absolutní tlak měří s ohledem na celkové vakuum, ve kterém nejsou žádné interagující molekuly. V nádobě, ve které bylo vytvořeno vakuum, nejsou žádné částice působící zevnitř na stěny nebo na předměty uvnitř..
Měřené tlaky mohou být vyšší nebo nižší než atmosférický tlak. V prvním případě mluvíme o měřicí tlak a ve druhém z vakuový tlak.
Normálně jsou tlaky měřené denně v pneumatikách a krevní tlak relativními tlaky, zatímco při měření atmosférického tlaku pomocí barometru se jedná o absolutní tlak.
Rejstřík článků
Jako relativní tlak je rozdíl mezi absolutním tlakem Pbřišní svaly a atmosférický tlak Pbankomat, je to rozdílový tlak nebo tlakový rozdíl. Při relativním tlaku Prel V angličtině je známý jako měřicí tlak PG a je dán vztahem:
Pbřišní svaly = Pbankomat + PG
Prel = Pbřišní svaly - Pbankomat
U tlaku se pascal používá jako jednotka měření mezinárodního systému jednotek, bez ohledu na to, zda se jedná o absolutní tlak nebo relativní tlak..
Pascal se rovná síle vyvíjené 1 newtonem na plochu 1 mdva, ale často se používají jiné jednotky, jako jsou milimetry rtuti, vody, anglosaské jednotky jako psi a další.
Jsou-li známy absolutní tlak v bodě a standardní atmosférický tlak, je relativní tlak odečtením mezi těmito dvěma hodnotami.
Předpokládejme například, že absolutní tlak v určitém systému je 305 kPa. S vědomím, že standardní atmosférický tlak je 101,3 kPa, je relativní tlak:
PG = Pbřišní svaly - Pbankomat = 305 - 101,3 kPa = 203,7 kPa
KPa nebo kilopascal je tisíckrát větší než jeden pascal. Používá se častěji, protože hodnoty tlaku jsou v řádu tisíců pascalů. Váha jablka je přibližně 1 newton a jeden pascal se rovná této síle rozložené na čtverec se stranou 1 metr. Používají se také další násobky, jako např megapascal (1 MPa = 1 x 106 Pa) nebo gigapascal (1 GPa = 1x 109 Pa).
Tlak v příkladu je přetlak, protože je nad atmosférickým tlakem, ale pod ním jsou absolutní tlaky. Například pokud má plyn v nádobě absolutní tlak 50 kPa, jeho relativní tlak je vakuový tlak, který vytváří sání:
PG = Pbřišní svaly - Pbankomat = 50 - 101,3 kPa = -51,3 kPa
V těchto příkladech byl použit standardní atmosférický tlak, kterým je tlak na hladině moře. Pokud je však při výpočtu požadována větší přesnost, lze použít místní atmosférický tlak, který se může lišit od 101,3 kPa, protože závisí na nadmořské výšce a dalších geografických podmínkách..
V textech jsou uvedené tlaky obvykle relativní, a pokud je nutné pracovat s absolutními tlaky, rozlišují se pomocí indexů, aby nedošlo k záměně..
V každém bodě uvnitř tekutiny, jako je voda, je tlak. Za předpokladu, že je voda nestlačitelná, zůstává její hustota konstantní a tlak se mění svisle.
To lze zkontrolovat odebráním malé části tekutiny ve formě silného disku dy který je v klidu uprostřed kapalné hmoty.
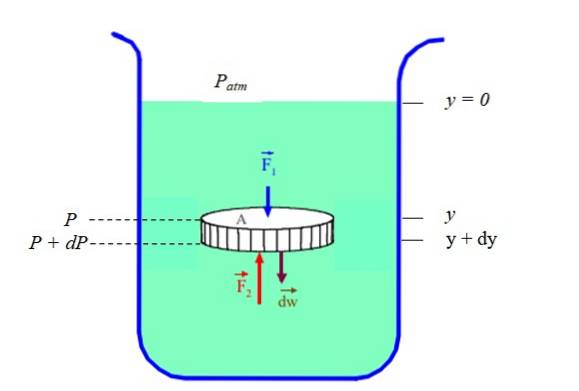
Síly na kruhových okrajích disku se ruší ve dvojicích, ale ne síly vyvíjené hmotou tekutiny nad a pod diskem: F1 Y Fdva. Kromě toho je nutné vzít v úvahu hmotnost kotouče s kapalinou dŽ v Newtonově druhém zákoně:
∑FY = Fdva - F1 - W = 0
Tyto síly lze vyjádřit pomocí tlaku, což je kolmá síla na jednotku plochy. Tímto způsobem máme tlak P, produkovaný silou F1:
F1 = P. A
Kde A je kruhová oblast disku. Podobně:
Fdva = (P + dP). NA
S P + dP tlak v hloubce y + dy. Hmotnost je dW = dm. G:
(P + dP). A - P. A - dm. g = 0
Hustota kapaliny je ρ = dm / dV, přičemž dV je objem disku kapaliny, daný A.dy. Takto:
(P + dP). A - P. A - ρA.dy .g = 0
Získaná rovnice je zjednodušena na:
dP - ρgdy = 0 → dP = ρgdy
Integrace obou stran z a1 do adva:
= Pdva - P1 = ρg (adva - Y1)
Termín Pdva - P1 je to tlakový rozdíl nebo rozdílový tlak. Pokud chceme znát tlak ve svislém souřadnicovém bodě y, uděláme to Y1 = 0, Ydva = a Y Pnebo = Pbankomat. S tímto budeme mít tlak vzhledem k uvedené hloubce, který závisí pouze na hloubce a:
Pdva - Pbankomat = ρgy ⇒ Prel = ρgy
Všichni jsme zažili tlak potápění do bazénu nebo k moři. Jaký je relativní tlak po ponoření do sladkovodního bazénu v hloubce 5 metrů? Použitím předchozího výrazu a vědomím, že hustota sladké vody je 1000 kg / m3, s g = 9,81 m / sdva relativní tlak je:
Prel = ρgy = 1000 x 9,81 x 5 Pa = 49050 Pa.
Pneumatiky vozidel jsou obvykle pod tlakem 32 psi. Jedná se o měřidlo nebo relativní tlak v librách na čtvereční palec, jednotka používaná v anglicky mluvících zemích. Mnoho měřidel je kalibrováno v těchto jednotkách. 32 psi se rovná 220632 Pa nebo 220 kPa.
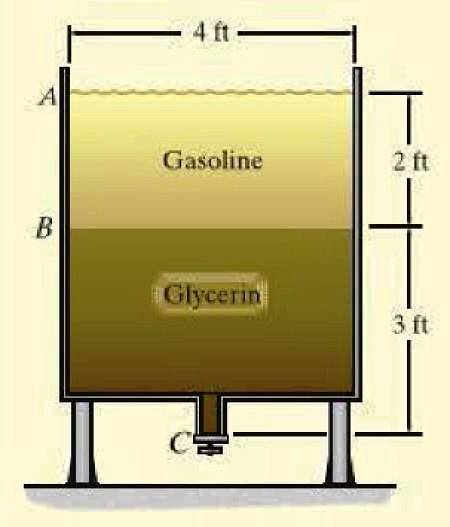
Nádrž obsahuje benzín a glycerin, dvě nemísitelné kapaliny (nemísí se) v uvedených výškách. Jaký je přetlak na dně nádrže? Specifické hmotnosti každé tekutiny označené řeckým písmenem γ jsou připojeny:
yplyn = 45,3 lb / ft3
ygly = 78,7 lb / ft3
Specifická hmotnost γ kapaliny je součinem její hustoty a gravitačního zrychlení, proto lze rovnici relativního tlaku vyjádřit takto:
Prel = γ.y.
Relativní tlak na dně nádrže je způsoben jak hmotností glycerinové kolony, tak hmotností benzinu a je nezávislý na tvaru nádrže:
Prel = γplyn . YAB + ygly . Ypřed naším letopočtem = (45,3 x 2 + 78,7 x 3) lb / ftdva = 326,7 lb / ftdva
Zatím žádné komentáře