
Vysvětlení první rovnovážné podmínky, příklady, cvičení
The první rovnovážný stav vyžaduje, aby vektorový součet všech sil působících na těleso byl nulový, aby byl v klidu (statická rovnováha) nebo s rovnoměrným přímočarým pohybem (dynamická rovnováha).
Tento součet sil není nic jiného než čistá síla, která působí na tělo, vyjádřená matematicky tímto způsobem:
Fsíť = 0
∑ F = 0

Ve vesmíru vede první rovnovážná podmínka ke třem rovnicím, jedné pro každou dimenzi:
∑ FX = 0; ∑ FY = 0 a ∑ Fz = 0
Když jsou tyto rovnice splněny, objekt se nepřekládá, nebo pokud ano, bude s konstantní rychlostí.
Když se díváme kolem sebe, uvědomujeme si, že se neustále snažíme uspokojit první podmínku rovnováhy, aby věci neklesly.
Proto se snaží kompenzovat gravitační přitažlivost Země pomocí podpěr, lan nebo podpěr některých, aby tak zůstaly věci na svém místě a neskončily na zemi..
Jindy je třeba zabránit tomu, aby vnější elektromagnetická pole zasahovala do činnosti elektrických obvodů a komunikačních zařízení. V tomto případě musí být v rovnováze elektrické náboje..
Rejstřík článků
- 1 Příklady
- 1.1 Budovy
- 1.2 Semafory a závěsné značky
- 1.3 Vodiče v elektrostatické rovnováze
- 1.4 Stropní svítidla
- 1.5 Knihy a předměty na stolech
- 1.6 Měření viskozity kapaliny
- 2 kroky k uplatnění první rovnovážné podmínky
- 3 Vyřešená cvičení
- 3.1 - Cvičení vyřešeno 1
- 3.2 - Cvičení vyřešeno 2
- 4 Témata zájmu
- 5 Reference
Příklady
Velké množství předmětů každodenní potřeby splňuje první podmínku rovnováhy, je třeba pečlivě dodržovat:
Budovy
Stavitelé hledají stabilitu konstrukcí, aby uživatelé zůstali v bezpečí. Cílem statiky je studovat podmínky pro vznik statické rovnováhy v budovách, mostech, silnicích a všech druzích konstrukcí..
Semafory a visící značky
Aby tato signalizační zařízení mohla plnit své funkce, musí zůstat pevná, proto jsou držena kabely, sloupy a tyčemi tak, aby byla splněna první rovnovážná podmínka..

Vodiče v rovnováze elektrostupřístřešek
Když vodivé materiály, jako je měď a jiné kovy, získají elektrický náboj, nastane brzy elektrostatická rovnováha, která ponechá přebytečný náboj na vodivém povrchu. Uvnitř elektrického pole je nula.
Tento efekt se často používá k izolaci elektrických a elektronických zařízení od vnějších polí pomocí takzvané Faradayovy klece. Klec je vyrobena z vodivého materiálu a obklopuje chráněné zařízení.
Během bouří automobily slouží jako Faradayovy klece tím, že chrání cestující před úrazy elektrickým proudem..
Stropní svítidla
V osvětlovacích systémech, jako jsou závěsné lampy, se první rovnovážný stav používá k jejich připevnění ke stropu, podlaze nebo stěně.

Knihy a předměty na stolech
Předměty umístěné na stolech a policích splňují první rovnovážnou podmínku. Normální síla, kterou podpěra působí na předměty, je odpovědná za vyrovnání hmotnosti.
Měření viskozity kapaliny
Aby se určila viskozita kapaliny, spadne do jejího vnitřku sférický předmět známého průměru a jeho rychlost se zpomalí kvůli odporu. Rychlost koule je konstantní, takže je v dynamické rovnováze.
Čím vyšší je viskozita kapaliny, tím nižší je rychlost, s jakou se koule pohybuje uvnitř.
Kroky k uplatnění první rovnovážné podmínky
-Vytvořte diagram volného těla, zobrazující všechny síly, které působí na tělo (vynechejte ty, které tělo působí na ostatní).
-Vyberte kartézský souřadný systém a zajistěte, aby síly byly pokud možno umístěny na kterékoli z os. Kladný směr je obvykle veden ve směru pohybu nebo možného pohybu.
-Určete kartézské složky každé síly.
-Uplatnění druhého Newtonova zákona pro každou složku, jak bylo stanoveno na začátku, tak zůstává soustavou rovnic.
-Vyřešte soustavu rovnic nastolených v předchozím kroku.
Vyřešená cvičení
- Vyřešené cvičení 1
Blok postavy, hmoty m, pohybuje se z kopce po nakloněné rovině pod úhlem θ s konstantní rychlostí. Vypočítejte hodnotu koeficientu kinetického tření μk, pokud je hmotnost bloku m = 5 kg a θ = 37 °.

Řešení
Prvním krokem je nakreslení diagramu volného těla a výběr kartézského souřadného systému pro vektorové vyjádření každé síly. Síly působící na blok jsou:
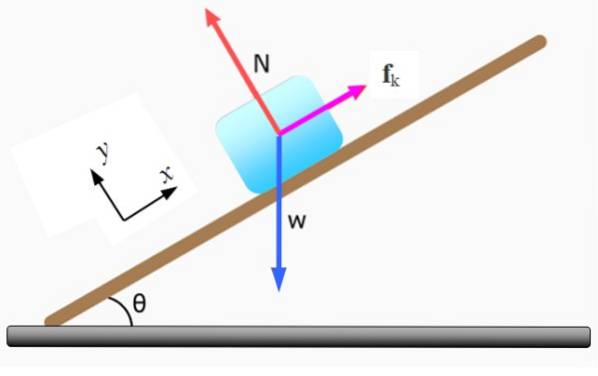
-Normální N vyvíjený nakloněnou rovinou, je kolmý k jeho povrchu.
-Váha Ž směřuje svisle dolů.
-Kinetické tření Fk který je proti pohybu. Pokud by neexistoval, tělo by se pohybovalo z kopce se zrychlením rovným g.senθ.
Jako váha Ž je nakloněn vzhledem k vybraným souřadným osám, musí být rozložen na jeho kartézské komponenty:
ŽX = mg sin 37º = 5 kg x 9,8 m / sdva x sin 37º = 29. 5 N.
ŽY = mg.cos 37º = 5 kg x 9,8 m / sdva x cos 37º = 39,1 N.
Nyní je použit Newtonův druhý zákon, který nastavuje každou částku na 0, protože bloku chybí zrychlení při pohybu s konstantní rychlostí:
∑ FY = N - WY = 0
∑ FX = WX - Fk = 0
Velikost kinetického tření je úměrná velikosti normály, koeficient kinetického tření je μk konstanta proporcionality.
Fk = μk N
Ve stejnou dobu:
N = WY = 39,1 N
Plus:
Fk = WX
Proto:
- 5 N = μk x 39,1 N.
μk = 29. 5 / 39,1 = 0,75
- Cvičení vyřešeno 2
Vypočítejte velikost napětí, která podporují semafor o hmotnosti 33 kg, jak je znázorněno na obrázku:
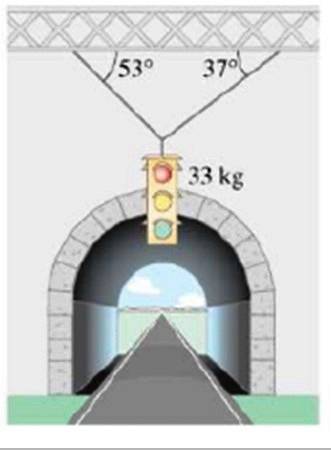
Řešení
Schéma volného těla je vytvořeno jak pro semafor, tak pro uzel, který drží kabely:
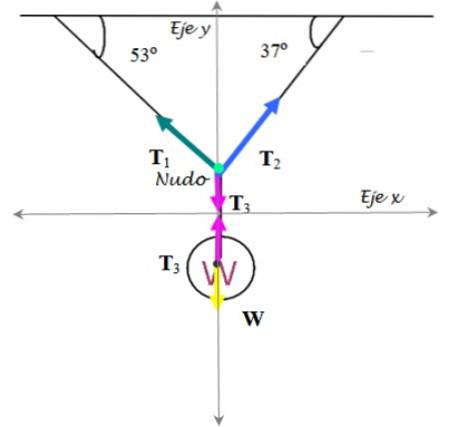
Semafor
Na to působí: napětí T3 nahoru a váha W dolů. Proto:
∑ FY = W - T3 = 0
Proto:
T3 = 33 kg x 9,8 m / sdva = 323,4 N
Uzel
Napětí se rozloží na jejich kartézské komponenty:
∑ FY = T1 hřích 53º + T.dva sen 37º - T3 = 0
∑ FX = Tdva cos 37º - T1 cos 53º = 0
A následující systém lineárních rovnic se získá se dvěma neznámými T1 a Tdva :
- 0,6 T.1 + 0,8 T.dva = 0
0,8 T.1 + 0,6 T.dva = 323,4
Řešení této soustavy rovnic je: T1 = 258,7 N a Tdva = 194,0 N
Témata zájmu
Rovnovážné podmínky.
Druhá rovnovážná podmínka.
Reference
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 4. Systémy částic. Upravil Douglas Figueroa (USB).
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume 1.
- Wikipedia. Statické (mechanické). Obnoveno z: es.wikipedia.org.



Zatím žádné komentáře