
Polytropické charakteristiky procesu, aplikace a příklady
A polytropický proces je termodynamický proces, ke kterému dochází, když je vztah mezi tlakem P a objem PROTI dána P.V.n zůstává konstantní. Exponent n je reálné číslo, obvykle mezi nulou a nekonečnem, ale v některých případech může být záporné.
Hodnota n přijme jméno index polytropy a je důležité zdůraznit, že během polytropického termodynamického procesu musí uvedený index udržovat pevnou hodnotu, jinak nebude proces považován za polytropní.

Rejstřík článků
- 1 Charakteristika polytropních procesů
- 2 Aplikace
- 2.1 Práce na polytropních procesech pro různé hodnoty n
- 3 Příklady polytropních procesů
- 3.1 - Příklad 1
- 3.2 - Příklad 2
- 4 Odkazy
Charakteristika polytropních procesů
Některé charakteristické případy polytropních procesů jsou:
- Izotermický proces (při konstantní teplotě T), ve kterém je exponent n = 1.
- Izobarický proces (při konstantním tlaku P), v tomto případě n = 0.
- Izochorický proces (při konstantním objemu V), pro který n = + ∞.
- Adiabatické procesy (při konstantní entropii S), ve kterých je exponent n = γ, kde γ je adiabatická konstanta. Tato konstanta je podíl mezi tepelnou kapacitou při konstantním tlaku Cp dělený tepelnou kapacitou při konstantním objemu Cv:
γ = Cp / Cv
- Jakýkoli jiný termodynamický proces, který není jedním z předchozích případů. ale to vyhovuje P.V.n = ctte se skutečným a konstantním polytropickým indexem n bude to také polytropický proces.
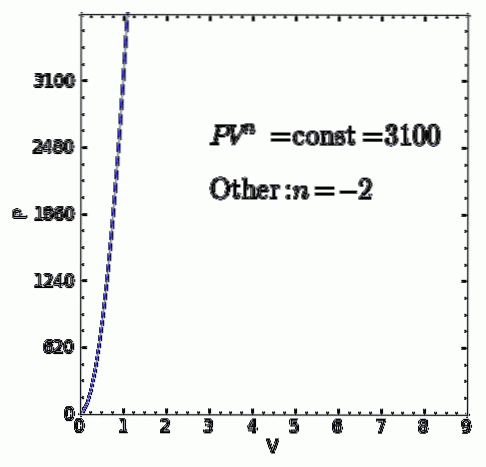
Aplikace
Jednou z hlavních aplikací polytropické rovnice je výpočet práce uzavřeného termodynamického systému, když přechází z počátečního stavu do konečného stavu kvazi-statickým způsobem, tj. Po posloupnosti rovnovážných stavů.
Práce na polytropních procesech pro různé hodnoty n
Pro n ≠ 1
Mechanická práce W prováděná uzavřeným termodynamickým systémem se vypočítá z výrazu:
W = .dP.dV
Kde P je tlak a V objem.
Stejně jako v případě polytropního procesu je vztah mezi tlakem a objemem:
P.V. n = konstantní = C.
Řešení pro P z předchozího výrazu, který jej nahradí v pracovním výrazu:
P = C /PROTI n
Necháme provádět mechanickou práci během polytropického procesu, který začíná v počátečním stavu 1 a končí v konečném stavu 2. To vše se objeví v následujícím výrazu:


C = P1 PROTI1n = Pdva PROTIdvan
Dosazením hodnoty konstanty do pracovního výrazu získáme:
W = (strdva PROTIdva - P1 PROTI1) / (1-n)
V případě, že lze pracovní látku modelovat jako ideální plyn, máme následující stavovou rovnici:
P.V = m.R.T.
Kde m je počet molů ideálního plynu a R je univerzální plynová konstanta.
Pro ideální plyn, který sleduje polytropický proces s indexem polytropy odlišným od jednoty a který prochází ze stavu s počáteční teplotou T1 do jiného stavu s teplotou Tdva máme, že odvedená práce je dána následujícím vzorcem:
W = m R (Tdva - T1) / (1-n)
Pro n → ∞
Podle vzorce pro práci získanou v předchozí části máme, že práce polytropního procesu s n = ∞ je nulová, protože výraz práce je dělen nekonečnem, a proto má výsledek tendenci k nule.
Dalším způsobem, jak dosáhnout tohoto výsledku, je vztah P1 PROTI1n = Pdva PROTIdvan, které lze přepsat takto:
(Str1/ Strdva) = (V.dva/ V1)n
Když vezmeme n-tý kořen v každém členu, získáme:
(PROTIdva/ V1) = (str1/ Strdva)(1 / n)
V případě, že n → ∞, máme (Vdva/ V1) = 1, což znamená, že:
PROTIdva = V1
To znamená, že objem se v polytropním procesu s n → ∞ nemění. Proto je objemový rozdíl dV v integrálu mechanické práce 0. Tyto typy polytropních procesů jsou také známé jako procesy izochorický, nebo procesy s konstantním objemem.
Pro n = 1
Opět máme výraz výraz pro práci:
W = ∫P dV
V případě polytropického procesu s n = 1 je vztah mezi tlakem a objemem:
P V = konstantní = C
Řešením pro P z předchozího výrazu a dosazením máme hotovou práci při přechodu z počátečního stavu 1 do konečného stavu 2:

A to:
W = C ln (Vdva/ V1).
Protože počáteční a konečný stav jsou dobře určeny, bude tomu tak i v případě. A to:
C = P1 PROTI1 = Pdva PROTIdva
Nakonec máme následující užitečné výrazy k nalezení mechanické práce polytropního uzavřeného systému, ve kterém n = 1.
W = P1 PROTI1 ln (V.dva/ V1) = Pdva PROTIdva ln (V.dva/ V1)
Pokud pracovní látka sestává z m moly ideálního plynu, pak lze použít stavovou rovnici ideálního plynu: P V = m.R.T.
V tomto případě, jako P.V.1 = ctte, máme, že polytropický proces s n = 1 je proces při konstantní teplotě T (izotermický), takže lze pro práci získat následující výrazy:
W = mR T1 ln (V.dva/ V1) = mR Tdva ln (V.dva/ V1)

Příklady polytropních procesů
- Příklad 1
Předpokládejme válec s pohyblivým pístem naplněným jedním kilogramem vzduchu. Zpočátku vzduch zaujímá objem V.1= 0,2 m3 při tlaku P1= 400 kPa. Po polytropickém procesu následuje n = γ = 1,4, jehož konečný stav má tlak Pdva = 100 kPa. Určete práci vykonanou vzduchem na pístu.
Řešení
Když se index polytropy rovná adiabatické konstantě, existuje proces, při kterém pracovní látka (vzduch) nevyměňuje teplo s okolím, a proto se entropie nemění..
Pro vzduch, diatomický ideální plyn, máme:
y = Cp / Cv, s Cp = (7/2) R a Cv = (5/2) R
Pak:
γ = 7/5 = 1,4
Pomocí vyjádření polytropického procesu lze určit konečný objem vzduchu:
PROTIdva = [(Strdva PROTI11.4) / Strdva](1 / 1,4) = 0,54 m3.
Nyní máme podmínky pro použití vzorce pro práci provedenou v polytropickém procesu pro n ≠ 1 získanou výše:
W = (strdva PROTIdva - P1 V1) / (1-n)
Nahrazením příslušných hodnot máme:
W = (100 kPa 0,54 m3 - 400 kPa 0,2 m3) / (1 - 1,4) = 65,4 kJ
- Příklad 2
Předpokládejme stejný válec z příkladu 1 s pohyblivým pístem naplněným jedním kilogramem vzduchu. Zpočátku vzduch zaujímá objem V1 = 0,2 m3 při tlaku P1 = 400 kPa. Ale na rozdíl od předchozího případu se vzduch izotermicky rozpíná a dosahuje konečného tlaku P2 = 100 kPa. Určete práci vykonanou vzduchem na pístu.
Řešení
Jak je vidět výše, izotermické procesy jsou polytropní procesy s indexem n = 1, takže je pravda, že:
P1 V1 = P2 V2
Tímto způsobem lze konečný objem snadno odloupnout a získat:
V2 = 0,8 m3
Pak pomocí pracovního výrazu získaného dříve pro případ n = 1 máme, že práce, kterou v tomto procesu provádí vzduch na pístu, je:
W = P1 V1 ln (V2 / V1) = 400000 Pa × 0,2 m3 ln (0,8 / 0,2) = 110,9 kJ.
Reference
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
- Cengel, Y. 2012. Termodynamika. 7. vydání. Mcgraw kopec.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 4. Kapaliny a termodynamika. Upravil Douglas Figueroa (USB).
- López, C. První zákon termodynamiky. Obnoveno z: culturacientifica.com.
- Knight, R. 2017. Fyzika pro vědce a inženýrství: strategický přístup. Pearson.
- Serway, R., Vulle, C. 2011. Základy fyziky. Učení 9. edice Cengage.
- Sevillská univerzita. Tepelné stroje. Obnoveno z: laplace.us.es.
- Wikiwand. Polytropický proces. Obnoveno z: wikiwand.com.


Zatím žádné komentáře