
Lineární programování k čemu je, modely, omezení, aplikace
The lineární programování je matematická metoda používaná k optimalizaci (maximalizaci nebo minimalizaci podle potřeby) funkce, jejíž proměnné podléhají omezením, pokud jsou funkce a omezení lineárně závislé na proměnných.
Obecně platí, že funkce, která má být optimalizována, modeluje praktickou situaci, jako je zisk výrobce, jehož vstupy, práce nebo stroje jsou omezené.

Jedním z nejjednodušších případů je maximalizace lineární funkce, která závisí pouze na dvou proměnných, které se nazývají rozhodovací proměnné. Může mít formu:
Z = k1x + kdvaY
S k1 a kdva konstantní. Tato funkce je známá jako Objektivní funkce. Samozřejmě existují situace, které si pro studium zaslouží více než dvě proměnné, které jsou složitější:
Z = k1X1 + kdvaXdva + k3X3 +... .
A omezení jsou také matematicky modelována systémem rovnic nebo nerovností, stejně lineárních v X a Y.
Soubor řešení tohoto systému se nazývá proveditelná řešení nebo proveditelné body. A mezi proveditelnými body je alespoň jeden, který optimalizuje objektivní funkci.
Lineární programování nezávisle vyvinuli americký fyzik a matematik George Dantzig (1914-2005) a ruský matematik a ekonom Leonid Kantorovich (1912-1986) krátce po druhé světové válce..
Metoda řešení problémů známá jako simplexní metoda Je to mozek Dantziga, který pracoval pro americké letectvo, University of Berkeley a Stanford University.

Rejstřík článků
- 1 Modely lineárního programování
- 2 Příklad modelu
- 3 Metody řešení
- 3.1 - Grafická nebo geometrická metoda
- 3.2 - Dantzigova simplexní metoda
- 4 Aplikace
- 5 Cvičení vyřešena
- 5.1 - Cvičení 1
- 5.2 - Cvičení 2
- 6 Reference
Modely lineárního programování
Prvky nezbytné k vytvoření modelu lineárního programování, vhodné pro praktickou situaci, jsou:
-Objektivní funkce
-Rozhodovací proměnné
-Omezení
V objektivní funkci definujete, čeho chcete dosáhnout. Předpokládejme například, že chcete maximalizovat své zisky z výroby určitých produktů. Poté je stanovena funkce „zisk“ podle ceny, za kterou se výrobky prodávají.
Matematicky lze tuto funkci vyjádřit zkráceně pomocí součtové notace:
Z = ∑ki Xi
V této rovnici ki jsou koeficienty a xi jsou rozhodovací proměnné.
Rozhodovací proměnné jsou prvky systému, jehož řízení je ovládáno, a jejich hodnoty jsou kladná reálná čísla. V navrhovaném příkladu jsou rozhodovacími proměnnými množství každého produktu, který má být vyroben, aby se dosáhlo maximálního zisku.
Nakonec máme omezení, kterými jsou lineární rovnice nebo nerovnice, pokud jde o rozhodovací proměnné. Popisují omezení problému, která jsou známá a mohou to být například množství suroviny dostupné při výrobě..
Druhy omezení
Můžete mít M počet omezení, počínaje od j = 1 dokud j = M. Matematicky jsou omezení tří typů:
- NAj = ∑ aij . Xi
- Bj ≥ ∑ bij . Xi
- Cj ≤ ∑ cij . Xi
První omezení je typu lineární rovnice a znamená, že hodnota Aj, který je znám, musí být respektován.
Zbývající dvě omezení jsou lineární nerovnosti a to znamená, že hodnoty B.j a C.j, je možné je respektovat nebo překročit, pokud je zobrazený symbol ≥ (větší nebo rovný) nebo respektovaný nebo nepřekročený, pokud je symbol ≤ (menší nebo roven).
Vzorový příklad
Oblasti použití jsou velmi různorodé, od obchodní administrativy po výživu, ale pro pochopení této metody je níže navržen jednoduchý model praktické situace se dvěma proměnnými..
Místní cukrárna je známá dvěma specialitami: koláčem z černého lesa a dortem s chapadly..
Při jeho přípravě vyžadují vejce a cukr. Do černého lesa potřebujete 9 vajec a 500 g cukru, zatímco pro chapadlovku potřebujete 8 vajec a 800 g cukru. Příslušné prodejní ceny jsou 8 $ a 10 $.
Problém je: Kolik koláčů každého druhu musí pečivo vydělat, aby maximalizovalo svůj zisk, protože má 10 kilogramů cukru a 144 vajec?
Rozhodovací proměnné
Rozhodovací proměnné jsou „x“ a „y“, které nabývají skutečných hodnot:
-x: počet koláčů v černém lese
-a: koláče typu chapadla.
Omezení
Omezení jsou dána skutečností, že počet koláčů je kladné množství a pro jejich přípravu je omezené množství suroviny..
Proto v matematické formě mají tato omezení formu:
- x ≥ 0
- a ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8 y ≤ 10
Omezení 1 a 2 tvoří nezápornost dříve exponované a všechny nerovnosti jsou lineární. V omezeních 3 a 4 nesmí být překročeny hodnoty: 144 vajec a 10 kg cukru.
Objektivní funkce
A konečně, objektivní funkcí je zisk získaný při výrobě „x“ množství koláčů z černého lesa plus „y“ množství chapadel. Vyrábí se vynásobením ceny množstvím vyrobených koláčů a přidáním pro každý typ. Jedná se o lineární funkci, kterou budeme nazývat G (x, y):
G = 8x + 10r
Metody řešení
Mezi různé metodiky řešení patří grafické metody, simplexní algoritmus a metoda vnitřních bodů..
- Grafická nebo geometrická metoda
Pokud máte problém se dvěma proměnnými, jako je ten v předchozí části, omezení určí polygonální oblast v rovině xy, volání proveditelný region nebo oblast životaschopnosti.
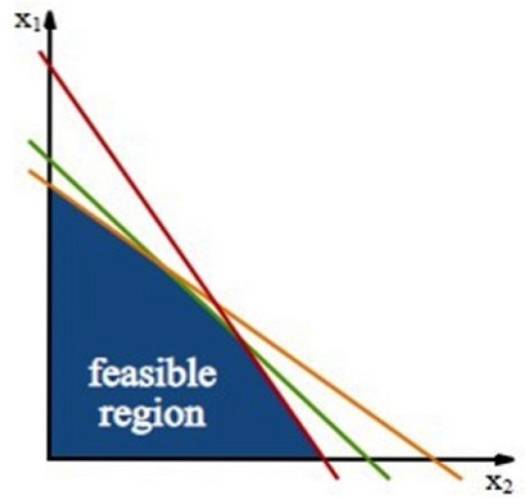
Tento region je budován pomocí omezující čáry, což jsou řádky získané z nerovností omezení, fungující pouze se znaménkem rovnosti.
V případě pekárny, která chce optimalizovat zisky, jsou hranice omezení:
- x = 0
- y = 0
- 9x + 8y = 144
- 0,5 x + 0,8 r = 10
Všechny body v oblasti ohraničené těmito řádky jsou možnými řešeními, takže je jich nekonečně mnoho. S výjimkou případu, kdy se ukáže, že je proveditelná oblast prázdná, nemá v takovém případě vzniklý problém žádné řešení.
Naštěstí pro problém s pečivem není proveditelná oblast prázdná, máme ji níže.
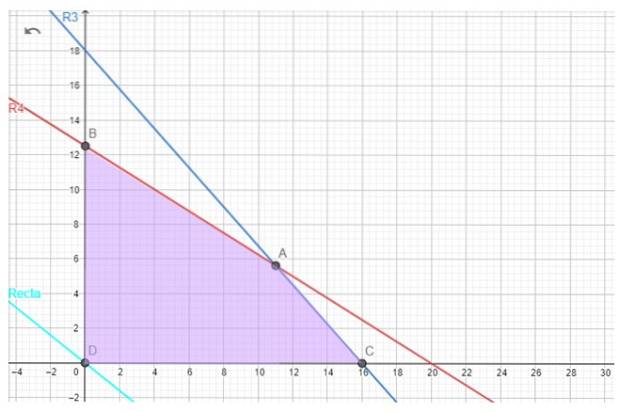
Optimální řešení, pokud existuje, je nalezeno pomocí objektivní funkce. Například když se snažíme najít maximální zisk G, máme následující řádek, který se nazývá iso-profit line:
G = k1x + kdvay → y = -k1x / kdva + G / kdva
S touto přímkou získáme všechny páry (x, y), které poskytují daný zisk G, takže existuje řada čar podle hodnoty G, ale všechny se stejným sklonem -k1 / kdva, jsou to tedy rovnoběžné čáry.
Optimální řešení
Nyní lze ukázat, že optimálním řešením lineárního problému je vždy krajní bod nebo vrchol realizovatelné oblasti. Pak:
Řada řešení je nejvzdálenější od původu a má alespoň jeden společný bod s proveditelnou oblastí.
Pokud má čára nejblíže k počátku celý segment společný s proveditelnou oblastí, říká se, že existují nekonečná řešení. K tomuto případu dochází, pokud je sklon izo-ziskové čáry stejný jako sklon kterékoli z ostatních přímek, které omezují region.
Pro naše pečivo jsou vrcholy kandidátů A, B a C..
- Dantzigova simplexní metoda
Grafická nebo geometrická metoda je použitelná pro dvě proměnné. Je to však komplikovanější, když existují tři proměnné, a je nemožné je použít pro větší počet proměnných..
Při řešení problémů s více než dvěma proměnnými platí: simplexní metoda, který se skládá z řady algoritmů pro optimalizaci objektivních funkcí. K provádění výpočtů se často používají matice a jednoduchá aritmetika.
Simplex metoda začíná výběrem proveditelného řešení a kontrolou, zda je optimální. Pokud ano, problém jsme již vyřešili, ale pokud tomu tak není, pokračujeme směrem k řešení blíže k optimalizaci. Pokud řešení existuje, algoritmus jej najde několika pokusy.
Aplikace
Lineární a nelineární programování se používá v mnoha oblastech, aby bylo možné činit nejlepší rozhodnutí, pokud jde o snižování nákladů a zvyšování zisků, které nejsou vždy peněžní, protože je lze měřit v čase, například pokud chcete minimalizovat čas nutný … provést řadu operací.
Zde je několik polí:
-V marketingu se používá k nalezení nejlepší kombinace médií (sociální sítě, televize, tisk a další) k inzerci určitého produktu.
-Pro přidělování odpovídajících úkolů pracovníkům společnosti nebo továrny nebo jejich harmonogramy.
-Při výběru nejživějšího jídla a při nejnižších nákladech v živočišné a drůbežářské výrobě.
Vyřešená cvičení
- Cvičení 1
Graficky vyřešte model lineárního programování uvedený v předchozích částech.
Řešení
Je nutné vytvořit graf množiny hodnot určených omezovacím systémem uvedeným v úloze:
- x ≥ 0
- a ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8 y ≤ 10
Oblast daná nerovnostmi 1 a 2 odpovídá prvnímu kvadrantu karteziánské roviny. Pokud jde o nerovnosti 3 a 4, začneme hledáním omezujících čar:
9x + 8y = 144
0,5 x + 0,8 r = 10 → 5 x + 8 r = 100
Realizovatelná oblast je čtyřúhelník, jehož vrcholy jsou body A, B, C a D.
Minimální zisk je 0, proto čára 8x + 10y = 0 je spodní hranice a izo-ziskové čáry mají sklon -8/10 = - 0,8.
Tato hodnota se liší od sklonů ostatních omezujících čar a protože je proveditelná oblast ohraničená, existuje jedinečné řešení.
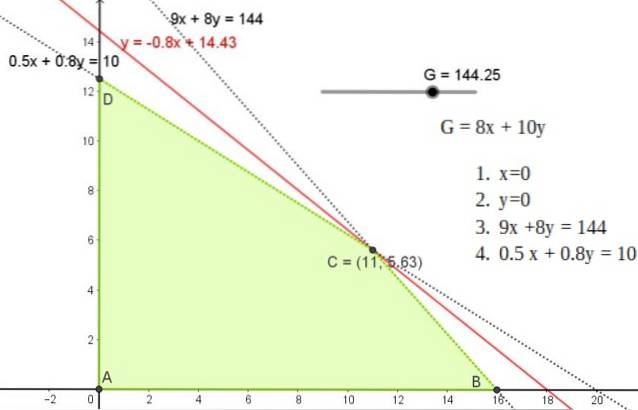
Toto řešení odpovídá přímce se sklonem -0,8, která prochází kterýmkoli z bodů A, B nebo C, jejichž souřadnice jsou:
A (11; 5,625)
B (0; 12,5)
C (16, 0)
Optimální řešení
Vypočítáme hodnotu G pro každý z těchto bodů:
-(11; 5,625): GNA = 8 x 11 + 10 x 5,625 = 144,25
-(0; 12,5): GB = 8 x 0 + 10 x 12,5 = 125
-(16, 0): GC = 8 x 16 + 10 x 0 = 128
Nejvyšší zisk je zjištěn při výrobě 11 koláčů z černého lesa a 5 625 obětních dortů. Toto řešení odpovídá řešení nalezenému prostřednictvím softwaru.
- Cvičení 2
Výsledek předchozího cvičení ověřte pomocí funkce Řešitel dostupné ve většině tabulek, jako je Excel nebo LibreOffice Calc, které pro optimalizaci v lineárním programování obsahují algoritmus Simplex pro optimalizaci..
Řešení
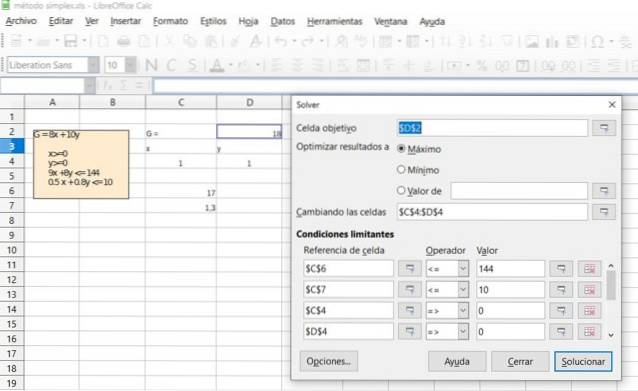
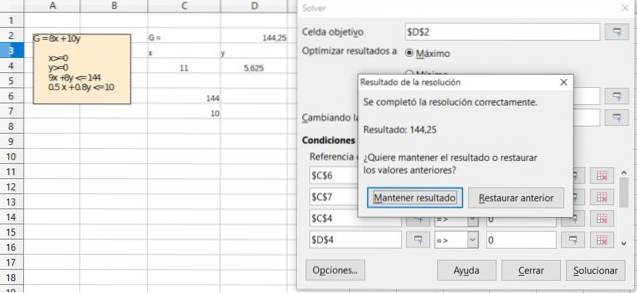
Reference
- Brilantní. Lineární programování. Obnoveno z: brilliant.org.
- Eppen, G. 2000. Operační výzkum v administrativní vědě. 5. Edice. Hala Prentice.
- Haeussler, E. 1992. Matematika pro management a ekonomiku. 2. místo Edice. Grupo Editorial Iberoamericana.
- Hiru. Lineární programování. Obnoveno z: hiru.eus.
- Wikipedia. Lineární programování. Obnoveno z: es. wikipedia.org.



Zatím žádné komentáře