Co je to vektorové množství? (S příklady)

Definuje vektorová veličina, nebo vektor, například ten, pro který je nutné specifikovat jak jeho velikost nebo modul (s příslušnými jednotkami), tak jeho směr.

Na rozdíl od vektorové veličiny má skalární veličina pouze velikost (a jednotky), ale žádný směr. Některé příklady skalárních veličin jsou mimo jiné teplota, objem objektu, délka, hmotnost a čas..

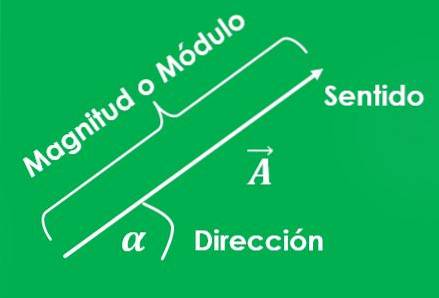
Rozdíl mezi vektorovým množstvím a skalárem

V následujícím příkladu se můžete naučit rozlišovat skalární veličinu od vektorové veličiny:

Rychlost 10 km / h je skalární veličina, zatímco rychlost 10 km / h na sever je vektorová veličina. Rozdíl je v tom, že v druhém případě je kromě velikosti specifikován směr.

Vektorové veličiny mají nekonečné množství aplikací, zejména ve světě fyziky.

Grafy a označení vektorového množství

Způsob, jak označit vektorovou veličinu, je umístit šipku (→) na písmeno, které se má použít, nebo napsat písmeno tučně (na).

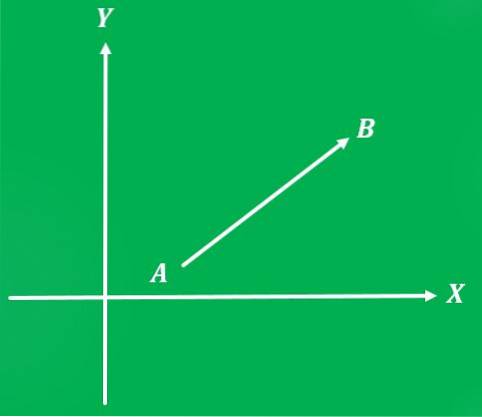
Ke grafu vektorové veličiny potřebujete referenční systém. V tomto případě bude jako referenční systém použita kartézská rovina.

Graf vektoru je čára, jejíž délka představuje velikost; a úhel mezi uvedenou čarou a osou X, měřený proti směru hodinových ručiček, představuje jeho směr.

Musíte určit, který je počátečním bodem vektoru a který je bodem příjezdu. Šipka je také umístěna na konec čáry ukazující na bod příjezdu, což označuje směr vektoru.

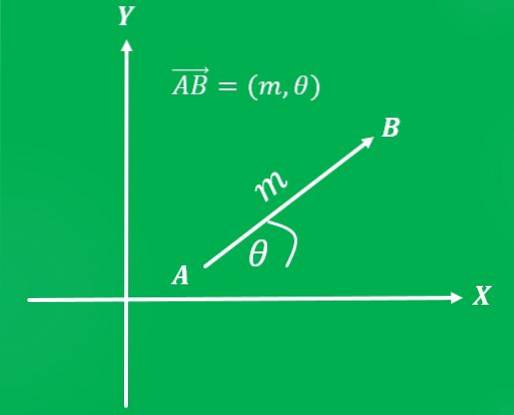
Jakmile je referenční systém zafixován, vektor lze zapsat jako uspořádaný pár: první souřadnice představuje jeho velikost a druhá souřadnice jeho směr..

Příklady

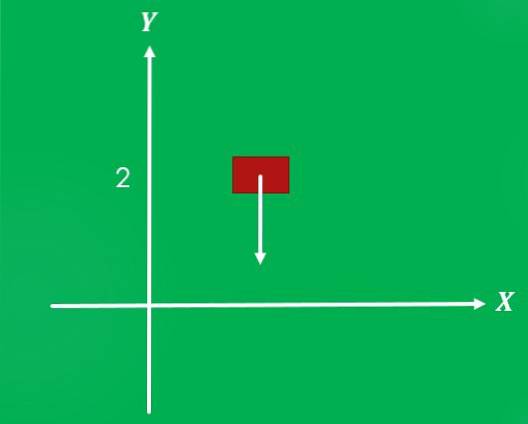
1 - Gravitace působící na předmět

Pokud je předmět umístěn ve výšce 2 metry nad zemí a je uvolněn, působí na něj gravitace o síle 9,8 m / s² a směru kolmém k zemi směrem dolů.

2 - Pohyb letounu

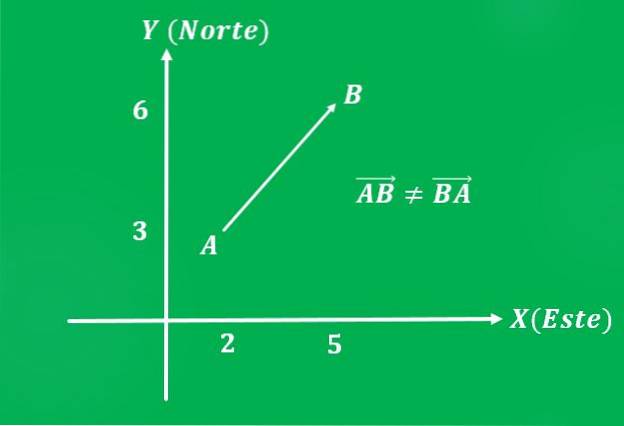
Letoun, který cestoval z bodu A = (2,3) do bodu B = (5,6) kartézského letadla, rychlostí 650 km / h (velikost). Směr trajektorie je 45 ° severovýchod (směr).

Je třeba poznamenat, že pokud je pořadí bodů obráceno, pak má vektor stejnou velikost a stejný směr, ale jiný smysl, který bude jihozápadní.

3 - Síla působící na objekt

Juan se rozhodne tlačit na židli silou 10 liber ve směru rovnoběžném se zemí. Možné směry použité síly jsou: doleva nebo doprava (v případě karteziánské roviny).

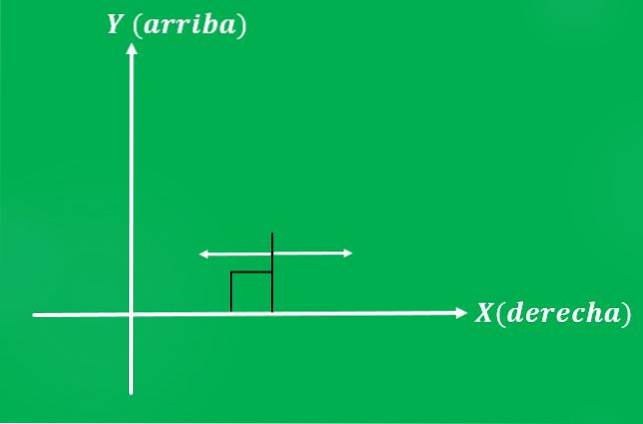
Stejně jako v předchozím příkladu vyvolá pocit, že se Juan rozhodne dát sílu, jiný výsledek.

To nám říká, že dva vektory mohou mít stejnou velikost a směr, ale mohou se lišit (vytvářejí různé výsledky).

Lze přidat a odečíst dva nebo více vektorů, pro které jsou k dispozici velmi užitečné výsledky, například zákon rovnoběžníku. Vektor můžete také vynásobit skalárem.

Reference

1. Barragan, A., Cerpa, G., Rodríguez, M., & Núñez, H. (2006). Fyzika pro středoškolskou kinematiku. Pearson Education.
2. Ford, K. W. (2016). Základní fyzika: Řešení cvičení. Světová vědecká nakladatelská společnost.
3. Giancoli, D. C. (2006). Fyzika: Principy s aplikacemi. Pearson Education.
4. Gómez, A. L. a Trejo, H. N. (2006). Fyzika l, konstruktivistický přístup. Pearson Education.
5. Serway, R. A., & Faughn, J. S. (2001). Fyzický. Pearson Education.
6. Stroud, K.A., & Booth, D. J. (2005). Vektorová analýza (Ilustrované vydání.). Industrial Press Inc..
7. Wilson, J. D. a Buffa, A. J. (2003). Fyzický. Pearson Education.