
Co jsou to koplanární vektory? (S vyřešenými cvičeními)
The koplanární vektory nebo koplanární jsou ty, které jsou obsaženy ve stejné rovině. Pokud existují pouze dva vektory, jsou vždy koplanární, protože existují nekonečné roviny, vždy je možné vybrat ten, který je obsahuje.
Pokud máte tři nebo více vektorů, je možné, že některé z nich nejsou ve stejné rovině jako ostatní, proto je nelze považovat za koplanární. Následující obrázek ukazuje sadu koplanárních vektorů označených tučně NA, B, C Y D:
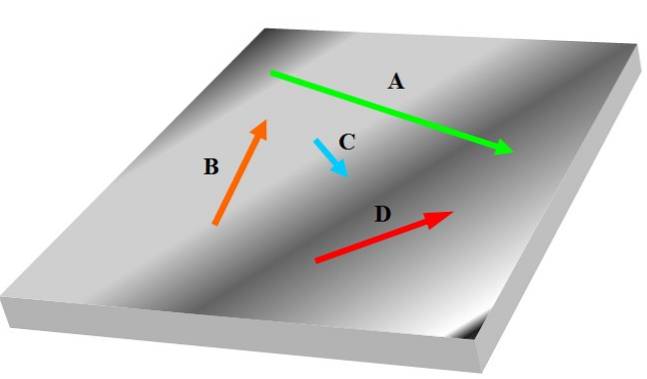
Vektory souvisejí s chováním a vlastnostmi příslušných fyzikálních veličin ve vědě a inženýrství; například rychlost, zrychlení a síla.
Síla vytváří různé efekty na objekt, když se mění způsob jeho aplikace, například změnou intenzity, směru a směru. I při změně pouze jednoho z těchto parametrů jsou výsledky značně odlišné..
V mnoha aplikacích, jak ve statice, tak v dynamice, jsou síly působící na tělo ve stejné rovině, proto jsou považovány za koplanární.
Rejstřík článků
- 1 Podmínky, aby vektory byly koplanární
- 1.1 Smíšený produkt mezi třemi vektory
- 2 Aplikace
- 2.1 Koplanární, souběžné a nekolineární síly
- 3 Vyřešená cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Podmínky pro to, aby vektory byly koplanární
Aby byly tři vektory koplanární, musí ležet ve stejné rovině, a to se stane, pokud splní některou z následujících podmínek:
-Vektory jsou paralelní, proto jsou jejich složky proporcionální a lineárně závislé.
-Váš smíšený produkt je neplatný.
-Pokud máte tři vektory a některý z nich lze zapsat jako lineární kombinaci ostatních dvou, jsou tyto vektory koplanární. Například vektor, který je výsledkem součtu dvou dalších, jsou tři ve stejné rovině.
Alternativně lze podmínku koplanárnosti stanovit následujícím způsobem:
U V w jsou koplanární, pokud existují tři (skalární) čísla α, β, γ taková, že αnebo + βproti + yw = 0 s (α, β, γ) jinými než (0, 0, 0)
Smíšený produkt mezi třemi vektory
Smíšený produkt mezi vektory je definován třemi vektory nebo, proti Y w, výsledkem je skalár, který je výsledkem provedení následující operace:
nebo · (proti X w) = nebo · (proti X w)
Nejprve se provede křížový produkt, který je v závorkách: proti X w, jehož výsledkem je normální vektor (kolmý) k rovině, ve které oba proti Co w.
Ano nebo je ve stejné rovině jako proti Y w, přirozeně musí být skalární součin (bodový součin) mezi u a uvedeným normálním vektorem 0. Tímto způsobem je ověřeno, že tři vektory jsou koplanární (leží ve stejné rovině).
Když smíšený produkt není nula, jeho výsledek se rovná objemu rovnoběžnostěnu, který má vektory nebo, proti Y w jako sousední strany.
Aplikace
Koplanární, souběžné a nekolineární síly
Silné stránky souběžně všechny jsou aplikovány na stejný bod. Pokud jsou také koplanární, mohou být nahrazeny jediným, který se nazývá výsledná síla a má stejný účinek jako původní síly.
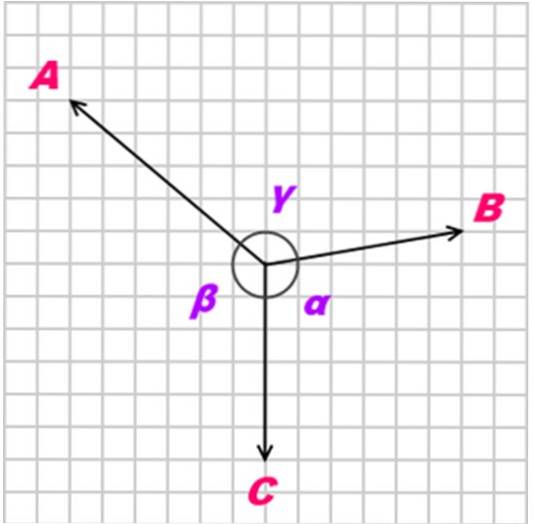
Pokud je těleso v rovnováze díky třem koplanárním silám, souběžným a ne kolineárním (ne paralelním), tzv. NA, B Y C, the Lamyho věta poukazuje na to, že vztah mezi těmito silami (velikostmi) je následující:
A / sin α = B / sin β = C / sin γ
S α, β a γ jako opačnými úhly k aplikovaným silám, jak je znázorněno na následujícím obrázku:
Vyřešená cvičení
-Cvičení 1
Najděte hodnotu k tak, aby následující vektory byly koplanární:
nebo = <-3, k, 2>
proti = <4, 1, 0>
w = <-1, 2, -1>
Řešení
Protože máme komponenty vektorů, použije se kritérium smíšeného produktu, proto:
nebo · (proti X w) = 0
Nejprve je vyřešen proti X w. Vektory budou vyjádřeny jednotkovými vektory i, j Y k které rozlišují tři kolmé směry v prostoru (šířka, výška a hloubka):
proti= 4 i + j + 0 k
w= -1 i + dvaj -1 k
proti X w = -4 (i x i) + 8 (i x j) - 4 (i x k) - (j x i) + dva (j x j) - dva (j x k) = 8 k + 4 j + k -dva i = -dva i + 4 j + 9 k
Nyní vezmeme v úvahu skalární součin mezi u a vektorem, který je výsledkem předchozí operace, nastavení operace rovné 0:
nebo (proti X w) = (-3 i + k j + dva k) · (-dva i + 4 j + 9 k) = 6 + 4k +18 = 0
24 + 4k = 0
Hledaná hodnota je: k = - 6
Takže vektor nebo to je:
nebo = <-3, -6, 2>
-Cvičení dva
Obrázek ukazuje objekt, jehož hmotnost je W = 600 N, visící v rovnováze díky kabelům umístěným v úhlech znázorněných na obrázku 3. Je možné v této situaci použít Lamyho větu? V každém případě najděte velikosti T1, Tdva Y T3 které umožňují rovnováhu.
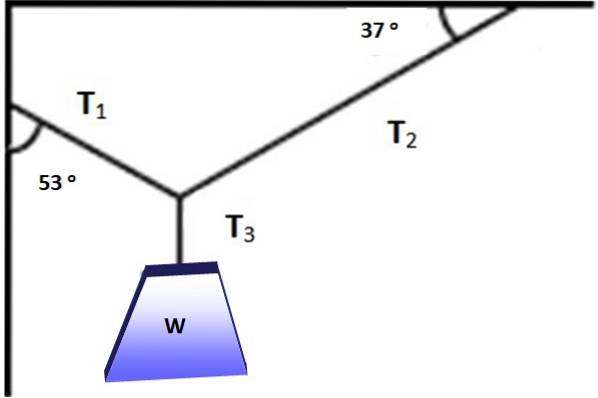
Řešení
Lamyho věta je v této situaci použitelná, uvažuje-li se uzel, na který jsou aplikována tři napětí, protože tvoří systém koplanárních sil. Nejprve se vytvoří diagram volného těla pro závěsné závaží, aby se určila velikost T3:
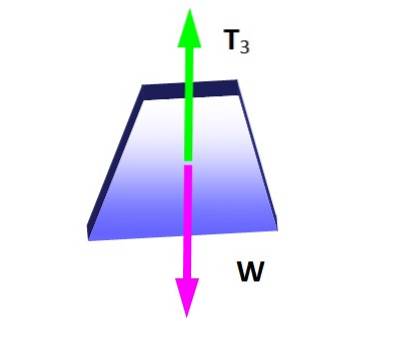
Z rovnovážné podmínky vyplývá, že:
T3 = W = 600 N
Úhly mezi silami jsou na následujícím obrázku označeny červeně, lze snadno ověřit, že jejich součet je 360 °. Nyní je možné použít Lamyho teorém, protože je známa jedna ze sil a tři úhly mezi nimi:
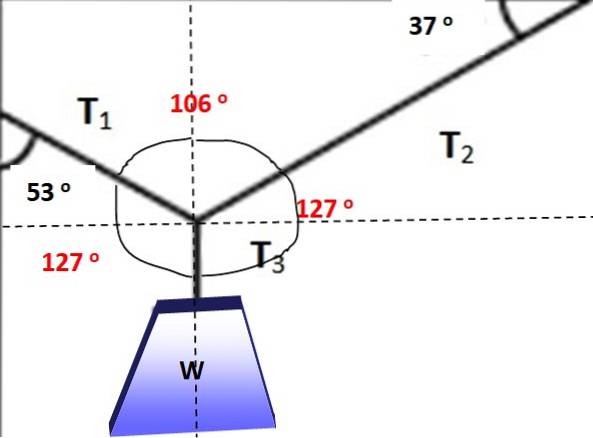
T1 / hřích 127 ° = W / hřích 106 °
Proto: T1 = hřích 127 ° (W / hřích 106 °) = 498,5 N
Opět platí, že Lamyho věta je aplikována na řešení pro Tdva:
Tdva / sin 127 = T.1 / hřích 127 °
Tdva = T1 = 498,5 N
Reference
- Figueroa, D. Series: Fyzika pro vědy a inženýrství. Svazek 1. Kinematika. 31-68.
- Fyzický. Modul 8: Vektory. Obnoveno z: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanics for Engineers. Statický. 6. vydání. Continental Publishing Company 28-66.
- Série McLean, W. Schaum. Mechanika pro inženýry: statika a dynamika. 3. vydání. McGraw Hill. 1-15.
- Wikipedia. Vektor. Obnoveno z: es.wikipedia.org.


Zatím žádné komentáře