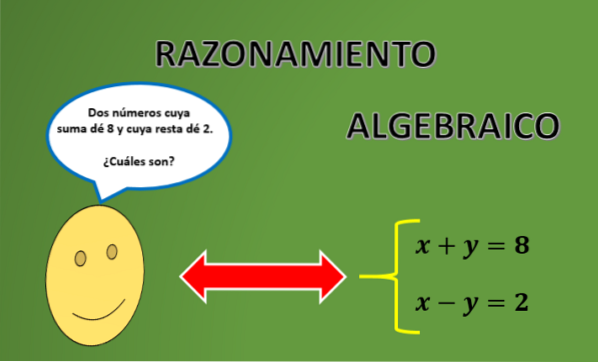
The algebraické uvažování V zásadě spočívá v komunikaci matematického argumentu prostřednictvím speciálního jazyka, který jej činí přísnějším a obecnějším, s využitím algebraických proměnných a operací definovaných mezi sebou. Charakteristikou matematiky je logická přísnost a abstraktní tendence použitá v jejích argumentech..
K tomu je nutné znát správnou „gramatiku“ použitou v tomto psaní. Algebraické uvažování se navíc vyhýbá nejasnostem v odůvodnění matematického argumentu, který je nezbytný k prokázání jakéhokoli výsledku v matematice..
Rejstřík článků
Algebraická proměnná je jednoduše proměnná (písmeno nebo symbol), která představuje určitý matematický objekt..
Například písmena x, y, z, se často používají k reprezentaci čísel, která splňují danou rovnici; písmena p, q r, která představují výrokové vzorce (nebo jejich příslušná velká písmena, která představují konkrétní výroky); a písmena A, B, X atd., která představují množiny.
Termín „proměnná“ zdůrazňuje, že dotyčný objekt není fixní, ale liší se. To je případ rovnice, ve které se proměnné používají k určení řešení, která jsou v zásadě neznámá.
Obecně lze algebraickou proměnnou považovat za písmeno, které představuje nějaký objekt, ať už je pevný nebo ne..
Stejně jako se algebraické proměnné používají k reprezentaci matematických objektů, můžeme také považovat symboly, které představují matematické operace.
Například symbol „+“ představuje operaci „přidání“. Dalšími příklady jsou různé symbolické notace logických spojek v případě výroků a množin..
Algebraický výraz je kombinací algebraických proměnných prostřednictvím dříve definovaných operací. Příkladem toho jsou základní operace sčítání, odčítání, násobení a dělení mezi čísly nebo logické spojky v propozicích a množinách..
Algebraické uvažování je odpovědné za vyjádření matematického uvažování nebo argumentu prostřednictvím algebraických výrazů.
Tato forma vyjádření pomáhá zjednodušit a zkrátit psaní, protože využívá symbolické notace a umožňuje lepší porozumění uvažování, které je prezentováno jasnějším a přesnějším způsobem.
Podívejme se na několik příkladů, které ukazují, jak se používá algebraické uvažování. Používá se velmi pravidelně k řešení logických a logických problémů, jak uvidíme brzy..
Vezměme si dobře známý matematický výrok „součet dvou čísel je komutativní.“ Podívejme se, jak můžeme tento výrok vyjádřit algebraicky: vzhledem ke dvěma číslům „a“ a „b“ tento výrok znamená, že a + b = b + a.
Úvaha použitá k interpretaci počátečního výroku a jeho vyjádření algebraickými termíny je algebraická úvaha..
Mohli bychom také zmínit slavný výraz „pořadí faktorů nemění součin“, který odkazuje na skutečnost, že součin dvou čísel je také komutativní, a algebraicky je vyjádřen jako axb = bxa.
Podobně mohou být (a ve skutečnosti jsou) vyjádřeny algebraicky asociativní a distribuční vlastnosti pro sčítání a součin, ve kterých je zahrnuto odčítání a dělení..
Tento typ uvažování zahrnuje velmi široký jazyk a používá se v mnoha různých kontextech. V každém případě je v těchto kontextech nutné rozpoznat vzorce, interpretovat věty a zobecnit a formalizovat jejich vyjádření v algebraických termínech s platným a postupným uvažováním..
Následuje několik logických problémů, které vyřešíme pomocí algebraického uvažování:
Jaké je číslo, které se po polovině rovná jedné?
K vyřešení tohoto typu cvičení je velmi užitečné reprezentovat hodnotu, kterou chceme určit pomocí proměnné. V tomto případě chceme najít číslo, které, vezmeme-li polovinu, dává jako výsledek číslo jedna. Označme x x hledané číslo.
„Vezmutí poloviny“ z čísla znamená jeho vydělení 2. Výše uvedené tedy lze vyjádřit algebraicky jako x / 2 = 1 a problém se scvrkává na řešení rovnice, která je v tomto případě lineární a je velmi snadné ji vyřešit. Řešení pro x získáme, že řešení je x = 2.
Závěrem je 2 číslo, které se při braní poloviny rovná 1.
Kolik minut do půlnoci, pokud před 10 minutami 5/3 toho, co zbývá nyní?
Označme „z“ počet minut do půlnoci (lze použít jakékoli jiné písmeno). Jinými slovy, právě teď zbývají „z“ minuty do půlnoci. To znamená, že před 10 minutami zbývalo do půlnoci „z + 10“ minut, což odpovídá 5/3 toho, co nyní chybí; tj. (5/3) z.
Poté se problém scvrkává na řešení rovnice z + 10 = (5/3) z. Vynásobením obou stran rovnosti 3 získáme rovnici 3z + 30 = 5z.
Nyní, když seskupujeme proměnnou "z" na jedné straně rovnosti, získáme 2z = 15, což znamená, že z = 15.
Je tedy 15 minut do půlnoci.
V kmeni, který praktikuje směny, existují tyto ekvivalence:
- Oštěp a náhrdelník jsou vyměněny za štít.
- Oštěp se rovná noži a náhrdelníku.
- Dva štíty jsou vyměněny za tři jednotky nožů.
Kolik náhrdelníků odpovídá kopí?
Sean:
Co = náhrdelník
L = kopí
E = štít
Cu = nůž
Máme tedy následující vztahy:
Co + L = E
L = Co + Cu
2E = 3 Cu
Takže problém se scvrkává na řešení soustavy rovnic. I když máme více neznámých než rovnic, lze tento systém vyřešit, protože od nás nepožadují konkrétní řešení, ale spíše jednu z proměnných jako funkci jiné. Musíme udělat pouze výraz „Co“ ve smyslu „L“.
Z druhé rovnice máme tu Cu = L - Co. Dosazením do třetí dostaneme E = (3L - 3Co) / 2. Nakonec dosazením do první rovnice a jejím zjednodušením se získá, že 5Co = L; to znamená, že kopí se rovná pěti náhrdelníkům.
Zatím žádné komentáře