
Vlastnosti osové symetrie, příklady a cvičení
The axiální symetrie Dochází k tomu, když se body figury shodují s body jiné figury pomocí přímky, která se nazývá osa symetrie. Nazývá se také radiální, rotační nebo válcová symetrie..
Obvykle se používá v geometrických obrazcích, ale v přírodě je snadno pozorovatelný, protože existují zvířata, jako jsou motýli, štíři, berušky nebo lidé, kteří představují axiální symetrii..

Rejstřík článků
- 1 Jak najít axiální symetrii
- 2 Vlastnosti axiální symetrie
- 3 Příklady axiální symetrie
- 4 cvičení osové symetrie
- 4.1 Cvičení 1
- 4.2 Cvičení 2
- 4.3 Cvičení 3
- 4.4 Cvičení 4
- 5 Reference
Jak najít axiální symetrii
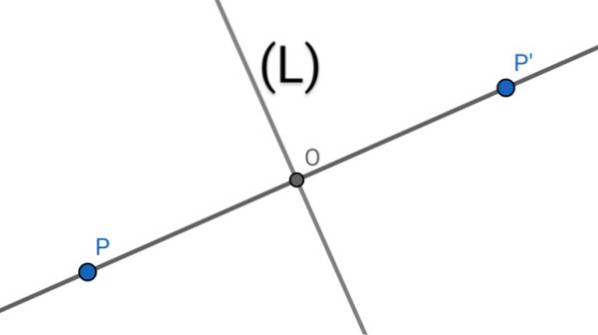
Chcete-li najít osovou symetrii P 'bodu P vzhledem k přímce (L), provedou se tyto geometrické operace:
1. - Kolmo na přímku (L), která prochází bodem P, je nakreslena.
2. - Zachycení dvou čar určuje bod O.
3. - Změří se délka segmentu PO, poté se tato délka zkopíruje přes čáru (PO) začínající od O ve směru od P do O určujícího bod P '.
4. - Bod P 'je osová symetrie bodu P vzhledem k ose (L), protože přímka (L) je střednicí segmentu PP', kde O je střed uvedeného segmentu.
Vlastnosti osové symetrie
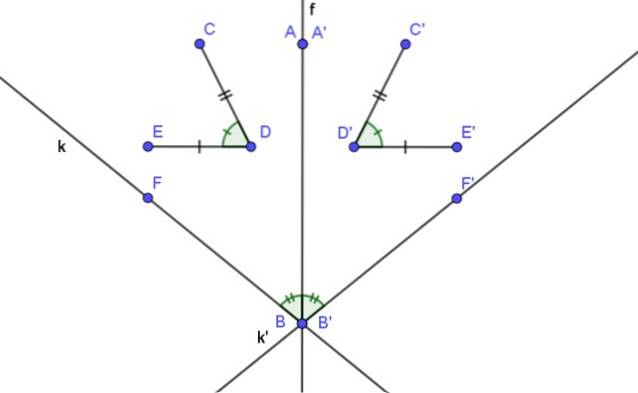
- Axiální symetrie je izometrická, to znamená, že jsou zachovány vzdálenosti geometrického útvaru a jeho odpovídající symetrie.
- Míra úhlu a jeho symetrie jsou stejné.
- Axiální symetrie bodu na ose symetrie je bod sám.
- Symetrická čára čáry rovnoběžné s osou symetrie je také čára rovnoběžná s uvedenou osou.
- Sekánková čára k ose symetrie má jako symetrickou linii další sečnickou linii, která protíná osu symetrie ve stejném bodě původní čáry.
- Symetrický obraz čáry je další čára, která svírá úhel s osou symetrie stejné míry jako u původní čáry.
- Symetrický obraz čáry kolmé k ose symetrie je další přímka, která překrývá první.
- Přímka a její osová symetrická čára tvoří úhel, jehož přímka je osou symetrie.
Příklady osové symetrie
Příroda vykazuje bohaté příklady axiální symetrie. Například můžete vidět symetrii tváří, hmyz, jako jsou motýli, odraz na klidných vodních plochách a zrcadlech nebo listí rostlin, mezi mnoha jinými..


Cvičení osové symetrie
Cvičení 1
Máme trojúhelník vrcholů A, B a C, jehož karteziánské souřadnice jsou A = (2, 5), B = (1, 1) a C = (3,3). Najděte kartézské souřadnice symetrického trojúhelníku kolem osy Y (osa souřadnic).
Řešení: Pokud má bod P souřadnice (x, y), pak jeho symetrický kolem osy souřadnic (osa Y) je P '= (- x, y). To znamená, že hodnota jeho úsečky se změní na znaménko, zatímco hodnota souřadnice zůstane stejná.
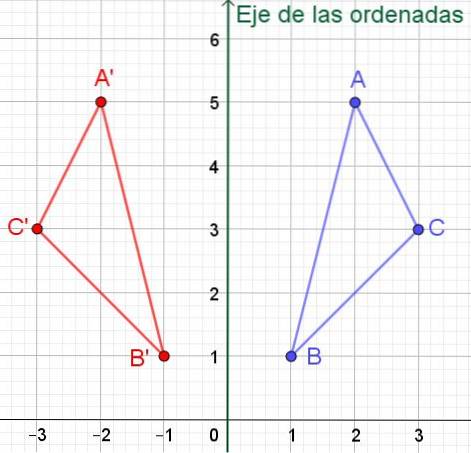
V tomto případě bude mít symetrický trojúhelník s vrcholy A ', B' a C 'souřadnice:
A '= (- 2, 5); B '= (- 1, 1) a C' = (- 3, 3), jak je vidět na obrázku 6.
Cvičení 2
S odkazem na trojúhelník ABC a jeho symetrický A'B'C 'z cvičení 1 zkontrolujte, zda mají odpovídající strany původního trojúhelníku a jeho symetrie stejnou délku.
Řešení: K nalezení vzdálenosti nebo délky stran použijeme euklidovský vzorec vzdálenosti:
d (A, B) = √ ((Bx - Ax) ^ 2 + (By - Ay) ^ 2) = √ ((1-2) ^ 2 + (1-5) ^ 2) = √ ((- 1 ) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
Délka odpovídající symetrické strany A'B 'se vypočítá níže:
d (A ', B') = √ ((Bx'-Ax ') ^ 2 + (By'-Ay') ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
Tímto způsobem je ověřeno, že osová symetrie zachovává vzdálenost mezi dvěma body. Postup lze opakovat pro další dvě strany trojúhelníku a jeho symetrickou kontrolu délky invariance. Například | AC | = | A'C '| = √5 = 2236.
Cvičení 3
Ve vztahu k trojúhelníku ABC a jeho symetrickému A'B'C 'z cvičení 1 zkontrolujte, zda odpovídající úhly původního trojúhelníku a jeho symetrie mají stejnou úhlovou míru.
Řešení: K určení míry úhlů BAC a B'A'C 'se nejprve vypočítá skalární součin vektorů AB s AC a pak tečkovaný produkt A'B ' s A'C '.
Pamatujte si, že:
A = (2, 5), B = (1, 1) a C = (3,3)
A '= (- 2, 5); B '= (- 1, 1) a C' = (- 3, 3).
Má to:
AB = <1-2, 1-5> Y AC = <3-2, 3-5>
podobně
A'B ' = <-1+2, 1-5> Y AC = <-3+2, 3-5>
Pak jsou nalezeny následující skalární produkty:
AB⋅AC = <-1, -4>⋅<1, -2> = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7
Podobně
A'B'⋅A'C ' = <1, -4>⋅<-1, -2> = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7
Míra úhlu BAC je:
∡BAC = ArcCos ( AB⋅AC / (|AB |⋅ |AC |)) =
ArcCos (7 / (4 123⋅2 236)) = 40,6 °
Podobně je míra úhlu B'A'C ':
∡B'A'C '= ArcCos ( A'B'⋅A'C ' / (|A'B '|⋅ |A'C '|)) =
ArcCos (7 / (4 123⋅2 236)) = 40,6 °
Závěrem lze říci, že axiální symetrie zachovává míru úhlu.
Cvičení 4
Dovolit být bod P souřadnic (a, b). Najděte souřadnice jeho osové symetrie P 'vzhledem k přímce y = x.
Řešení: Budeme nazývat (a ', b') souřadnice symetrického bodu P 'vzhledem k přímce y = x. Střed M segmentu PP 'má souřadnice ((a + a') / 2, (b + b ') / 2) a je také na přímce y = x, takže platí následující rovnost:
a + a '= b + b'
Na druhé straně má segment PP 'sklon -1, protože je kolmý na přímku y = x se sklonem 1, takže platí následující rovnost:
b - b '= a' -a
Při řešení dvou předchozích rovností a 'a b' se dospělo k závěru, že:
a '= b a to b' = a.
To znamená, že vzhledem k bodu P (a, b) je jeho osová symetrie vzhledem k přímce y = x P '(b, a).
Reference
- Arce M., Blázquez S a další. Transformace letadla. Obnoveno z: educutmxli.files.wordpress.com
- Výpočet cc. Axiální symetrie. Obnoveno z: Calclo.cc
- Superprof. Axiální symetrie. Obnoveno z: superprof.es
- wikipedia. Axiální symetrie. Obnoveno z: es.wikipedia.com
- wikipedia. Kruhová symetrie. Obnoveno z: en.wikipedia.com



Zatím žádné komentáře