
Osmičková historie systému, systém číslování, převody
The osmičkový systém je systém pozičního číslování základny osm (8); to znamená, že se skládá z osmi číslic, kterými jsou: 0, 1, 2, 3, 4, 5, 6 a 7. Každá číslice osmičkového čísla může mít tedy libovolnou hodnotu od 0 do 7. Osmičková čísla jsou tvořena z binárních čísel.
Je tomu tak proto, že jeho základna je přesná síla dvou (2). To znamená, že čísla, která patří do osmičkové soustavy, jsou vytvořena, když jsou seskupena do tří po sobě jdoucích číslic, seřazených zprava doleva, čímž se získá jejich desetinná hodnota..

Rejstřík článků
- 1 Historie
- 2 Osmičkový systém číslování
- 3 Převod z osmičkové soustavy na desetinnou
- 3.1 Příklad 1
- 3.2 Příklad 2
- 4 Převod z desítkové soustavy na osmičkovou
- 4.1 Příklad
- 5 Převod z osmičkové soustavy na binární
- 6 Převod z binárního na osmičkový systém
- 7 Převod z osmičkového na šestnáctkový a naopak
- 7.1 Příklad
- 8 Reference
Příběh
Osmý systém má původ ve starověku, kdy lidé počítali zvířata od osmi do osmi rukou.
Například pro počítání počtu krav ve stáji se jedna začala počítat pravou rukou a spojením palce s malíčkem; pak k spočítání druhého zvířete byl palec spojen s ukazováčkem a tak dále se zbývajícími prsty každé ruky, dokud nebylo dokončeno 8.
Existuje možnost, že ve starověku byl osmičkový systém číslování používán před desetinnou čárkou, aby bylo možné počítat interdigitální mezery; tj. spočítat všechny prsty kromě palců.
Později byl zaveden osmičkový systém číslování, který vznikl z binárního systému, protože potřebuje mnoho číslic, aby představoval pouze jedno číslo; od té doby byly vytvořeny osmičkové a šestihranné systémy, které nevyžadují tolik číslic a lze je snadno převést na binární systém.
Osmičkový systém číslování
Osmičkový systém se skládá z osmi číslic od 0 do 7. Tyto mají stejnou hodnotu jako v případě desítkové soustavy, ale jejich relativní hodnota se mění v závislosti na poloze, kterou zaujímají. Hodnota každé pozice je dána mocnostmi základny 8.
Pozice číslic v osmičkovém čísle mají následující váhy:
84, 83, 8dva, 81, 80, osmička, 8-1, 8-dva, 8-3, 8-4, 8-5.
Největší osmičková číslice je 7; tímto způsobem se při počítání v tomto systému zvýší pozice číslice z 0 na 7. Když je dosaženo 7, recykluje se na 0 pro další počítání; tímto způsobem se zvýší pozice další číslice. Například pro počítání sekvencí bude v osmičkové soustavě:
- 0, 1, 2, 3, 4, 5, 6, 7, 10.
- 53, 54, 55, 56, 57, 60.
- 375, 376, 377, 400.
Na osmičkovou soustavu se vztahuje základní věta, která je vyjádřena následovně:
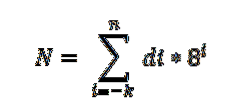
V tomto výrazu di představuje číslici vynásobenou výkonem základny 8, která označuje hodnotu místa každé číslice, stejným způsobem, jakým je uspořádána v desítkové soustavě.
Například máte číslo 543.2. Chcete-li jej přenést do osmičkové soustavy, rozdělí se takto:
N = ∑ [(5 * 8dva) + (4 * 81) + (3 *80) + (2 *8-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)
N = 320 +32 + 2 + 0,25 = 354 + 0,25d
Tímto způsobem musíte 543.2co = 354,25d. Dolní index q označuje, že se jedná o osmičkové číslo, které může být také reprezentováno číslem 8; a dolní index d odkazuje na desetinné číslo, které může být také reprezentováno číslem 10.
Převod z osmičkové soustavy na desítkovou
Chcete-li převést číslo z osmičkové soustavy na její ekvivalent v desítkové soustavě, musíte každou osmičkovou číslici vynásobit její místní hodnotou, počínaje zprava.
Příklad 1
7328 = (7* 8dva) + (3* 81) + (2* 80) = (7 * 64) + (3 * 8) + (2 * 1)
7328= 448 +24 +2
7328= 47410
Příklad 2
26.98 = (2 *81) + (6* 80) + (9* 8-1) = (2 * 8) + (6 * 1) + (9 * 0,125)
26.98 = 16 + 6 + 1,125
26.98= 23 12510
Převod z desítkové soustavy na osmičkovou
Desetinné celé číslo lze převést na osmičkové číslo pomocí metody opakovaného dělení, kde se celé desetinné číslo dělí 8, dokud se kvocient nebude rovnat 0, a zbytky každého dělení budou představovat osmičkové číslo..
Zbytky jsou seřazeny od poslední do první; to znamená, že první zbytek bude nejméně významná číslice osmičkového čísla. Tímto způsobem bude nejvýznamnější číslice poslední zbytek..
Příklad
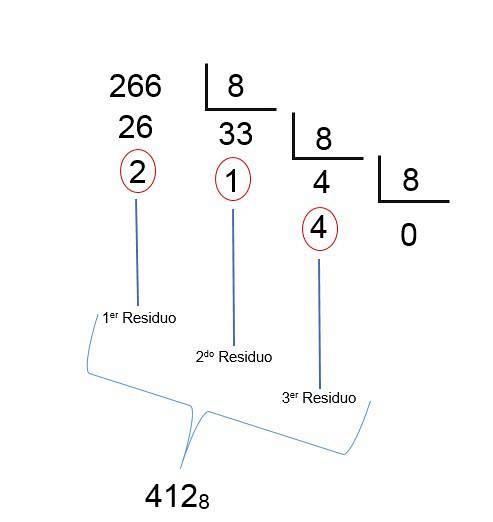
Osmičkové desetinné číslo 26610
- Vydělte desetinné číslo 266 číslem 8 = 266/8 = 33 + zbytek 2.
- Pak vydělte 33 o 8 = 33/8 = 4 + zbytek 1.
- Vydělte 4 8 = 4/8 = 0 + zbytek 4.
Protože s posledním dělením je získán kvocient menší než 1, znamená to, že byl nalezen výsledek; Zbývající části musíte objednat pouze obráceně, a to tak, že osmičkové číslo desetinné č. 266 je 412, jak je vidět na následujícím obrázku:
Převod z osmičkové soustavy na binární
Převod z osmičky na binární se provádí převedením osmičkové číslice na ekvivalentní binární číslici, která se skládá ze tří číslic. Existuje tabulka, která ukazuje, jak se převádí osm možných číslic:
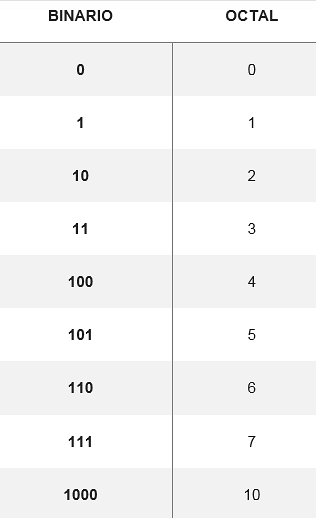
Z těchto převodů můžete změnit libovolné číslo z osmičkové soustavy na binární, například pro převod čísla 5728 jejich ekvivalenty jsou prohledány v tabulce. Musí tedy:
58 = 101
78= 111
dva8 = 10
Proto 5728 je v binárním systému ekvivalentní 10111110.
Převod z binárního na osmičkový
Proces převodu binárních celých čísel na osmičková celá čísla je inverzní operací předchozího procesu.
To znamená, že bity binárního čísla jsou seskupeny do dvou skupin po třech bitech, počínaje zprava doleva. Poté se provede převod z binárního na osmičkový pomocí předchozí tabulky.
V některých případech nebude mít binární číslo skupiny 3 bitů; k jeho dokončení se přidá jedna nebo dvě nuly nalevo od první skupiny.
Chcete-li například změnit binární číslo 11010110 na osmičkové, postupujte takto:
- Skupiny 3 bitů jsou vytvářeny počínaje zprava (poslední bit):
11010110
- Protože první skupina je neúplná, přidá se úvodní nula:
011010110
- Převod se provádí z tabulky:
011 = 3
010 = 2
110 = 6
Binární číslo 011010110 se tedy rovná 3268.
Převod z osmičkového na šestnáctkový a naopak
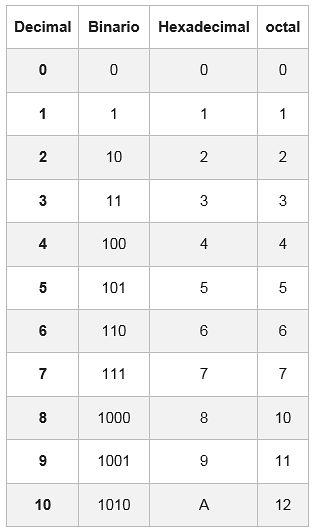
Chcete-li přejít z osmičkového čísla na hexadecimální systém nebo z hexadecimálního systému na osmičkový, je nutné nejprve převést číslo na binární a poté na požadovaný systém.
K tomu existuje tabulka, kde je každá hexadecimální číslice představována svým ekvivalentem v binární soustavě složená ze čtyř číslic.
V některých případech nebude mít binární číslo skupiny 4 bitů; k jeho dokončení se přidá jedna nebo dvě nuly nalevo od první skupiny
Příklad
Převést osmičkové číslo 1646 na šestnáctkové číslo:
- Převést číslo z osmičkového na binární
18 = 1
68 = 110
48 = 100
68 = 110
- Tak, 16468 = 1110100110.
- Chcete-li převést z binárního na hexadecimální, nejprve se seřadí ve skupině 4 bitů, počínaje zprava doleva:
11 1010 0110
- První skupina je doplněna nulami, takže může mít 4 bity:
0011 1010 0110
- Převod se provádí z binárního na hexadecimální systém. Ekvivalence se nahrazují pomocí tabulky:
0011 = 3
1010 = A
0110 = 6
Osmičkové číslo 1646 tedy odpovídá 3A6 v hexadecimálním systému..
Reference
- Bressan, A. E. (1995). Úvod do číslovacích systémů. Argentinská obchodní univerzita.
- Harris, J. N. (1957). Úvod do binárních a osmičkových číslovacích systémů: Lexington, Mass. Armed Services Technical Information Agency.
- Kumar, A. A. (2016). Základy digitálních obvodů. Učení Pvt.
- Peris, X. C. (2009). Single operační systémy.
- Ronald J. Tocci, N. S. (2003). Digitální systémy: principy a aplikace. Pearson Education.


Zatím žádné komentáře