Teleskopický součet, jak je řešen a cvičení řešena

The součet teleskopický je obor operací s číselnými řadami. Řeší součet prvků z počáteční hodnoty na „n“ výrazů, jejichž argument se řídí některým z následujících vzorů:

(F_X - F_{x + 1}); (F._{x + 1}  - F_X)

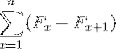
Jako také:

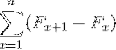
Představují souhrn prvků, které jsou při vývoji podrobeny zrušení opačných výrazů. Umožnění definování následující rovnosti pro teleskopické součty:

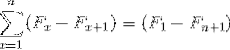
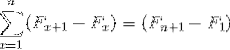
Jeho název vychází ze vztahu k vzhledu klasického dalekohledu, který lze složit a rozložit, a to zejména změnou jeho rozměru. Stejným způsobem lze shrnout teleskopické součty, které mají nekonečnou povahu, do zjednodušeného výrazu:

F₁ - F_{n + 1}

Rejstřík článků

• 1 Ukázka
• 2 Jak vyřešit?
  • 2.1 Rozklad na jednoduché zlomky
• 3 Historie
• 4 cvičení
  • 4.1 Cvičení 1
  • 4.2 Cvičení 2
• 5 Reference

Demonstrace

Při vývoji součtu termínů je eliminace faktorů zcela zřejmá. Kde pro každý z případů se v další iteraci objeví opačné prvky.

První případ (F._X - F_{x + 1}), protože proces funguje homologním způsobem pro (F_{x + 1}-F_X).

Při vývoji prvních 3 hodnot 1, 2, 3 je pozorován trend zjednodušování

X₁     (F₁ - F_{1 + 1}) = F₁ - F_dva

X_dva     (F_dva - F_{2 + 1}) = F_dva - F₃

X₃     (F₃ - F_{3 + 1}) = F₃ - F₄

Kde při vyjádření součtu popsaných prvků:

X₁ + X_dva + X₃ = F₁ - F_dva + F_dva - F₃ + F₃ - F₄

Je pozorováno, že F termíny_dva a F₃ jsou popsány společně s jejich protiklady, což činí jejich zjednodušení nevyhnutelným. Stejným způsobem se pozoruje, že výrazy F₁ a F₄ zůstat.

Pokud byl součet vytvořen z x = 1 až x = 3, znamená to, že prvek F₄ odpovídá obecnému výrazu F_{n + 1.}

Takto prokazující rovnost:

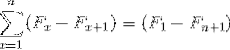
Jak je to vyřešeno?

Účelem teleskopických součtů je usnadnit práci, takže není nutné vytvářet nekonečné množství termínů nebo zjednodušovat příliš dlouhý řetězec doplňků..

Pro jeho řešení bude nutné vyhodnotit pouze F podmínky₁ a F_{n + 1}. Tyto jednoduché substituce tvoří konečný výsledek součtu.

Souhrn podmínek nebude vyjádřen, stane se nezbytným pouze pro prokázání výsledku, ale nikoli pro normální výpočetní proces.

Důležité je všimnout si konvergence číselných řad. Někdy nebude souhrnný argument vyjádřen teleskopicky. V těchto případech je implementace alternativních factoringových metod velmi častá..

Charakteristická faktorizační metoda v teleskopických přídavcích je metoda jednoduchých zlomků. K tomu dochází, když je původní zlomek rozložen na součet několika zlomků, kde je teleskopický obrazec (F_X - F_{x + 1}) nebo (F._{x + 1}  - F_X).

Rozklad na jednoduché zlomky

Pro ověření konvergence numerické řady je velmi běžné transformovat racionální výrazy metodou jednoduchých zlomků. Cílem je modelovat graf do tvaru teleskopického součtu..

Například následující rovnost představuje rozklad na jednoduché zlomky:

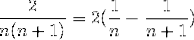
Při vývoji číselné řady a použití odpovídajících vlastností má výraz následující podobu:

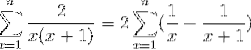
Kde je teleskopický tvar (F_X - F_{x + 1}).

Postup je docela intuitivní a spočívá v nalezení hodnot čitatele, které bez porušení rovnosti umožňují oddělit produkty, které jsou ve jmenovateli. Rovnice, které vznikají při určování těchto hodnot, jsou vyvolány podle srovnání mezi oběma stranami rovnosti.

Tento postup je při vývoji cvičení 2 pozorován krok za krokem.

Příběh

Je docela nejisté, abychom mohli definovat historický okamžik, ve kterém byly představeny teleskopické součty. Jeho implementaci však začíná být vidět v sedmnáctém století, ve studiích numerických řad prováděných Leibnizem a Huygensem..

Oba matematici, zkoumající součty trojúhelníkových čísel, si začínají všímat trendů v konvergenci určité řady po sobě jdoucích prvků. Ještě zajímavější je však začátek modelování těchto výrazů v prvcích, které na sebe nemusí nutně navazovat.

Ve skutečnosti výraz použitý dříve k označení jednoduchých zlomků:

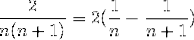
Byl představen Huygensem a okamžitě upoutal Leibnizovu pozornost. Kdo v průběhu času mohl pozorovat konvergenci k hodnotě 2. Aniž by o tom věděl, implementoval formát teleskopického součtu.

Výcvik

Cvičení 1

Definujte, ke kterému výrazu konverguje následující součet:

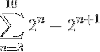
Při ručním vývoji součtu je pozorován následující vzorec:

(dva³ - dva⁴) + (2⁴ - dva⁵) + (2⁵ - dva⁶)… (Dva¹⁰ - dva^jedenáct)

Kde jsou faktory ze 2⁴ až 2¹⁰ Představují kladné a záporné části, díky nimž je jejich zrušení evidentní. Jedinými faktory, které nebudou zjednodušeny, budou první „2³“A poslední„ 2^jedenáct".

Tímto způsobem se při implementaci kritéria teleskopického součtu získá toto:

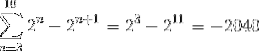
Cvičení 2

Transformujte argument na souhrn teleskopického typu a definujte konvergenci řady:

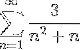
Jak je uvedeno v prohlášení, první věcí, kterou musíte udělat, bude rozložit se na jednoduché zlomky, abyste přepracovali argument a vyjádřili ho teleskopickým způsobem..

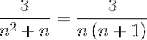
Musíte najít 2 zlomky, jejichž jmenovatelem jsou „n“ a „n + 1“, kde níže použitá metoda musí získat hodnoty čitatele, které splňují rovnost.

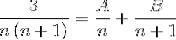
Pokračujeme k definování hodnot A a B. Nejprve přidáme zlomky.

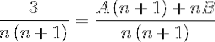
Poté se jmenovatelé zjednoduší a vytvoří se lineární rovnice.

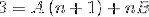
V dalším kroku se provede výraz vpravo, dokud se nedosáhne vzoru srovnatelného s „3“ vlevo..

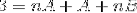
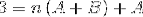
Chcete-li definovat rovnice, které se mají použít, je třeba porovnat výsledky obou stran rovnosti. To znamená, že na levé straně nejsou pozorovány žádné hodnoty proměnné n, tímto způsobem se A + B bude muset rovnat nule.

A + B = 0; A = -B

Na druhou stranu se konstantní hodnota A bude muset rovnat konstantní hodnotě 3.

A = 3

Proto.

A = 3 a B = -3

Jakmile jsou hodnoty čitatele pro jednoduché zlomky již definovány, je součet přepočítán.

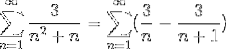
Tam, kde již bylo dosaženo obecné formy teleskopického součtu. Teleskopická řada je vyvinuta.

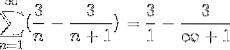
Kde při dělení velmi velkým číslem se výsledek přiblíží a přiblíží nule, pozorujeme konvergenci řady k hodnotě 3.

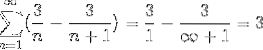
Tento typ řady nemohl být vyřešen žádným jiným způsobem, kvůli nekonečnému počtu iterací, které definují problém. Tato metoda však spolu s mnoha dalšími rámuje obor studia numerických řad, jehož cílem je určit hodnoty konvergence nebo definovat divergenci uvedených řad..

Reference

1. Infinitesimální lekce kalkulu. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. EDITUM, 1994.
2. Integrální počet: Sekvence a řada funkcí. Antonio Rivera Figueroa. Grupo Editorial Patria, 21. října. 2014.
3. Kurz kalkulu a reálné analýzy. Sudhir R. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5. června. 2006.
4. Nekonečná série. Tomlinson Fort. Clarendon Press, 1930.
5. Základy teorie nekonečných procesů. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorporated, 1923.