
Vysvětlení Bayesovy věty, aplikace, cvičení
The Bayesova věta je postup, který nám umožňuje vyjádřit podmíněnou pravděpodobnost náhodné události A dané B, pokud jde o rozdělení pravděpodobnosti události B dané A a rozdělení pravděpodobnosti pouze A.
Tato věta je velmi užitečná, protože díky ní můžeme spojit pravděpodobnost, že dojde k události A, s vědomím, že došlo k B, s pravděpodobností, že nastane opak, tj. Že B nastane vzhledem k A.
Bayesova věta byla stříbrným návrhem reverenda Thomase Bayese, anglického teologa z 18. století, který byl také matematikem. Byl autorem několika teologických prací, ale v současnosti je známý několika matematickými pojednáními, mezi nimiž vyniká již zmíněná Bayesova věta..
Bayes se touto větou zabýval v práci nazvanou „Esej k řešení problému v nauce o šancích“, publikované v roce 1763, a na které bylo vyvinuto velké množství studií s aplikacemi v různých oblastech znalostí.
Rejstřík článků
- 1 Vysvětlení
- 2 Aplikace Bayesovy věty
- 2.1 Vyřešená cvičení
- 3 Odkazy
Vysvětlení
Za prvé, pro lepší pochopení této věty jsou nezbytné některé základní pojmy teorie pravděpodobnosti, zejména věta o násobení pro podmíněnou pravděpodobnost, která uvádí, že
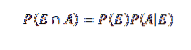
Pro E a A libovolné události vzorového prostoru S.
A definice oddílů, která nám říká, že pokud máme A1 ,NAdva,…, TOn události vzorového prostoru S, budou tvořit oddíl S, pokud Ai se vzájemně vylučují a jejich svazkem je S..
Vzhledem k tomu nechť B je další událost. Takže můžeme vidět B jako
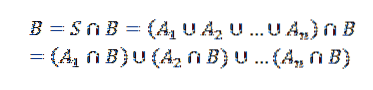
Kde je Ai protínající se s B jsou vzájemně se vylučující události.
A v důsledku toho,
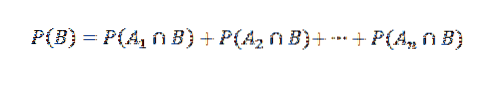
Poté uplatnění věty o násobení
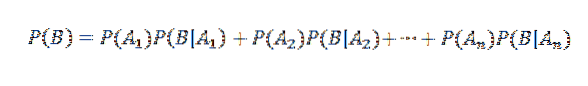
Na druhou stranu je podmíněná pravděpodobnost Ai dané B definována
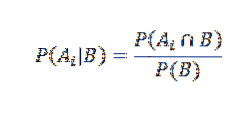
Vhodným nahrazením to máme pro všechny i
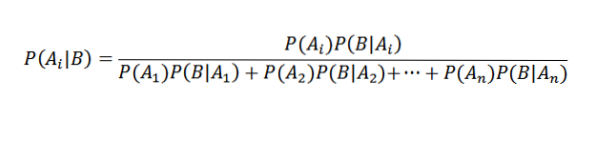
Aplikace Bayesovy věty
Díky tomuto výsledku se výzkumným skupinám a různým korporacím podařilo vylepšit systémy založené na znalostech..
Například při studiu nemocí může Bayesova věta pomoci rozeznat pravděpodobnost, že se choroba objeví u skupiny lidí s danou charakteristikou, přičemž jako údaje vezme globální míru výskytu nemoci a převahu uvedených charakteristik v obou zdraví a nemocní lidé.
Na druhou stranu ve světě vyspělých technologií ovlivnila velké společnosti, které díky tomuto výsledku vyvinuly „znalostní“ software.
Jako každodenní příklad máme pomocníka Microsoft Office. Bayesova věta pomáhá softwaru vyhodnotit problémy, které uživatel představuje, a určit, jaké rady je třeba poskytnout, a být tak schopen nabídnout lepší službu podle zvyklostí uživatele.
Je třeba poznamenat, že tento vzorec byl až do nedávné doby ignorován, je to hlavně proto, že když byl tento výsledek vyvinut před 200 lety, měl pro ně malé praktické využití. V dnešní době však vědci díky velkému technologickému pokroku našli způsoby, jak tento výsledek uplatnit v praxi.
Vyřešená cvičení
Cvičení 1
Společnost vyrábějící mobilní telefony má dva stroje A a B. 54% vyrobených mobilních telefonů vyrábí stroj A a zbytek stroj B. Ne všechny vyrobené mobilní telefony jsou v dobrém stavu.
Podíl vadných mobilních telefonů vyrobených A je 0,2 a B je 0,5. Jaká je pravděpodobnost, že je mobilní telefon z této továrny vadný? Jaká je pravděpodobnost, že s vědomím, že je mobilní telefon vadný, pochází ze stroje A?
Řešení
Zde máte experiment, který se provádí ve dvou částech; v první části dojde k událostem:
A: buňka vyrobená strojem A.
B: buňka vyrobená strojem B.
Protože stroj A produkuje 54% mobilních telefonů a zbytek vyrábí stroj B, vyplývá z toho, že stroj B produkuje 46% mobilních telefonů. Jsou uvedeny pravděpodobnosti těchto událostí, jmenovitě:
P (A) = 0,54.
P (B) = 0,46.
Události druhé části experimentu jsou:
D: vadný mobilní telefon.
E: nezávadný mobilní telefon.
Jak je uvedeno v prohlášení, pravděpodobnosti těchto událostí závisí na výsledku získaném v první části:
P (D | A) = 0,2.
P (D | B) = 0,5.
Pomocí těchto hodnot lze také určit pravděpodobnosti doplňků těchto událostí, to znamená:
P (E | A) = 1 - P (D | A)
= 1 - 0,2
= 0,8
Y
p (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Událost D lze nyní zapsat takto:
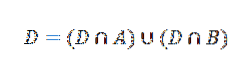
Použití věty o násobení pro výsledky podmíněné pravděpodobnosti:
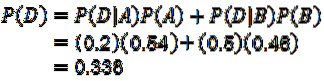
Tím je zodpovězena první otázka.
Nyní musíme pouze vypočítat P (A | D), pro které platí Bayesova věta:
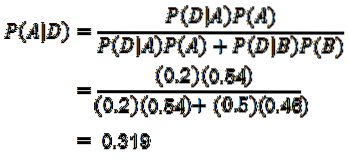
Díky Bayesově teorému lze konstatovat, že pravděpodobnost, že byl mobilní telefon vyroben strojem A, s vědomím, že je mobilní telefon vadný, je 0,319.
Cvičení 2
Tři krabice obsahují černé a bílé koule. Složení každého z nich je následující: U1 = 3B, 1N, U2 = 2B, 2N, U3 = 1B, 3N.
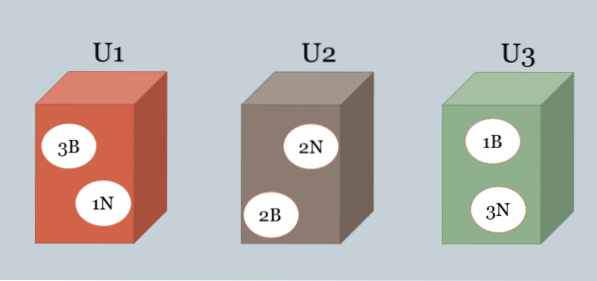
Jedno z polí je vybráno náhodně a náhodně je nakreslen míč, který se ukáže jako bílý. Jaký rámeček byl s největší pravděpodobností vybrán?
Řešení
Pomocí U1, U2 a U3 také představujeme vybrané pole.
Tyto události tvoří oddíl S a je ověřeno, že P (U1) = P (U2) = P (U3) = 1/3, protože volba pole je náhodná.
Pokud B = nakreslená koule je bílá, budeme mít P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4 .
To, co chceme získat, je pravděpodobnost, že míč byl vytažen z krabice Ui s vědomím, že uvedený míč byl bílý, tj. P (Ui | B), a zjistěte, která ze tří hodnot byla nejvyšší z toho boxu byla s největší pravděpodobností těžba bílé koule.
Aplikování Bayesovy věty na první z polí:
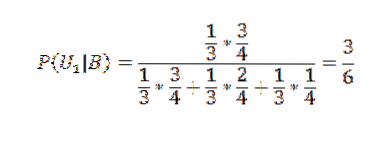
A pro další dva:
P (U2 | B) = 2/6 a P (U3 | B) = 1/6.
Poté je první z polí ten, který má nejvyšší pravděpodobnost, že bude vybrán pro extrakci bílé koule..
Reference
- Kai Lai Chung. Teorie základní stability se stochastickými procesy. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskrétní matematika a její aplikace. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Pravděpodobnost a statistické aplikace. S.A. MEXICKÁ ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Vyřešené problémy diskrétní matematiky. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teorie a pravděpodobnostní problémy. McGRAW-HILL.



Zatím žádné komentáře