
Bolzanova věta Vysvětlení, aplikace a cvičení
The Bolzanova věta stanoví, že pokud je funkce spojitá ve všech bodech uzavřeného intervalu [a, b] a je pravda, že obraz „a“ a „b“ (pod funkcí) mají opačné znaky, bude existovat alespoň jeden bod "C" v otevřeném intervalu (a, b) takovým způsobem, že funkce vyhodnocená v "c" bude rovna 0.
Tuto větu vyslovil filozof, teolog a matematik Bernard Bolzano v roce 1850. Tento vědec, narozený v dnešní České republice, byl jedním z prvních matematiků v historii, který formálně prokázal vlastnosti spojitých funkcí..
Rejstřík článků
- 1 Vysvětlení
- 2 Demo
- 3 K čemu slouží?
- 4 Vyřešená cvičení
- 4.1 Cvičení 1
- 4.2 Cvičení 2
- 5 Reference
Vysvětlení
Bolzanova věta je také známá jako věta o mezilehlých hodnotách, která pomáhá při určování konkrétních hodnot, zejména nul, určitých reálných funkcí reálné proměnné.
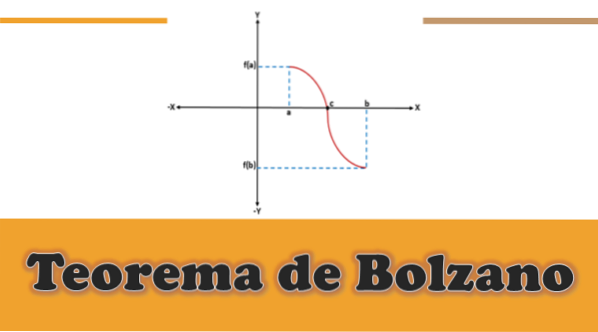
V dané funkci f (x) pokračuje - to znamená, že f (a) a f (b) jsou spojeny křivkou -, kde f (a) je pod osou x (je záporná) a f ( b) nad osou x (je kladná) nebo naopak, graficky bude na ose x mezní bod, který bude představovat střední hodnotu „c“, která bude mezi „a“ a „B“ a hodnota f (c) se bude rovnat 0.
Grafickou analýzou Bolzanovy věty lze vidět, že pro každou spojitou funkci f definovanou na intervalu [a, b], kde f (a)*f (b) je menší než 0, v intervalu (a, b) bude alespoň jeden kořen „c“ této funkce.
Tato věta nestanovuje počet bodů v tomto otevřeném intervalu, pouze uvádí, že existuje alespoň 1 bod.
Demonstrace
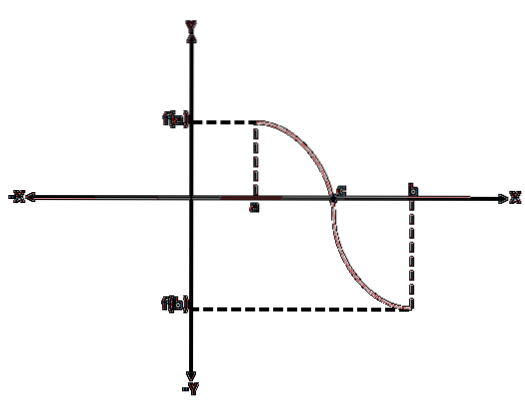
K prokázání Bolzanovy věty se bez ztráty obecnosti předpokládá, že f (a) < 0 y f(b) > 0; mezi hodnotami „a“ a „b“ tedy může být mnoho hodnot, pro které f (x) = 0, ale je nutné pouze ukázat, že existuje jedna.
Začneme hodnocením f ve středu (a + b) / 2. Pokud f ((a + b) / 2) = 0, pak důkaz končí zde; jinak je f ((a + b) / 2) kladné nebo záporné.
Jedna z polovin intervalu [a, b] je zvolena tak, že znaky funkce vyhodnocené v extrémech jsou odlišné. Tento nový interval bude [a1, b1].
Nyní, pokud f vyhodnocené ve středu [a1, b1] není nula, provede se stejná operace jako dříve; to znamená, že je zvolena polovina tohoto intervalu, která splňuje podmínku znaků. Nechť je tento nový interval [a2, b2].
Pokud budete v tomto procesu pokračovat, budete mít dvě sekvence an a bn, které:
an roste a bn klesá:
a ≤ a1 ≤ a2 ≤… ≤ an ≤…. ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Pokud se vypočítá délka každého intervalu [ai, bi], budeme mít:
b1-a1 = (b-a) / 2.
b2-a2 = (b-a) / 2².
... .
bn-an = (b-a) / 2 ^ n.
Proto je limit jako n sklon k nekonečnu (bn-an) roven 0.
Pomocí toho, že an roste a je omezeno a bn je zmenšeno a omezeno, máme, že existuje hodnota "c" taková, že:
a ≤ a1 ≤ a2 ≤… ≤ an ≤… .≤ c ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Limit an je „c“ a limit bn je také „c“. Proto vzhledem k libovolnému δ> 0 vždy existuje „n“, takže interval [an, bn] je obsažen v intervalu (c-δ, c + δ).
Nyní je třeba ukázat, že f (c) = 0.
Pokud f (c)> 0, pak protože f je spojité, existuje ε> 0 takové, že f je kladné po celý interval (c-ε, c + ε). Jak však bylo řečeno výše, existuje hodnota „n“ taková, že f mění znaménko v [an, bn] a navíc [an, bn] je obsaženo v (c-ε, c + ε), což je rozpor.
Pokud f (c) < 0, entonces como f es continua, existe un ε >0 takové, že f je v celém intervalu záporné (c-ε, c + ε); ale existuje hodnota „n“ taková, že f změní přihlášení v [an, bn]. Ukazuje se, že [an, bn] je obsažen v (c-ε, c + ε), což je také rozpor.
Proto f (c) = 0 a to je to, co jsme chtěli ukázat.
K čemu to je?
Z jeho grafické interpretace se Bolzanova věta používá k nalezení kořenů nebo nul v spojité funkci, pomocí půlení (aproximace), což je metoda přírůstkového hledání, která vždy vydělí intervaly 2.
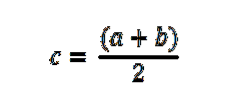
Potom se provede interval [a, c] nebo [c, b], kde dojde ke změně znaménka, a proces se opakuje, dokud není interval menší a menší, aby se přiblížil k požadované hodnotě; to znamená na hodnotu, kterou funkce dělá 0.
Stručně řečeno, abychom aplikovali Bolzanovu větu a našli tak kořeny, omezili nuly funkce nebo poskytli řešení rovnice, provedou se následující kroky:
- Ověřuje se, zda f je spojitá funkce na intervalu [a, b].
- Pokud není uveden interval, je třeba najít jeden, kde je funkce spojitá.
- Ověřuje se, zda extrémy intervalu dávají při hodnocení na f opačné znaky.
- Pokud nejsou získána žádná opačná znaménka, musí být interval rozdělen na dva podintervaly pomocí středního bodu.
- Vyhodnoťte funkci ve středu a ověřte, zda je splněna Bolzanova hypotéza, kde f (a) * f (b) < 0.
- V závislosti na znaménku (kladném nebo záporném) nalezené hodnoty se proces opakuje s novým podintervalem, dokud není splněna výše uvedená hypotéza..
Vyřešená cvičení
Cvičení 1
Určete, zda je funkce f (x) = xdva - 2, má alespoň jedno reálné řešení v intervalu [1,2].
Řešení
Máme funkci f (x) = xdva - 2. Jelikož se jedná o polynom, znamená to, že je spojitý v libovolném intervalu.
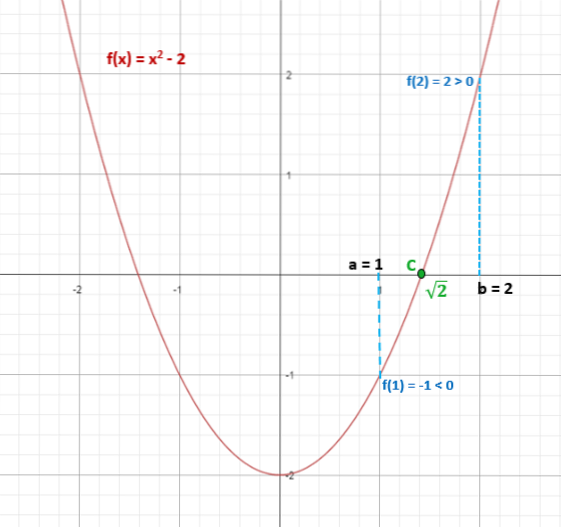
Je žádáno, aby určil, zda má reálné řešení v intervalu [1, 2], takže nyní je potřeba pouze nahradit extrémy intervalu ve funkci, abychom poznali jejich znaménko a věděli, zda splňují podmínku odlišnosti:
f (x) = xdva - dva
f (1) = 1dva - 2 = -1 (negativní)
f (2) = 2dva - 2 = 2 (pozitivní)
Proto znaménko f (1) ≠ znaménko f (2).
Tím je zajištěno, že do intervalu [1,2], ve kterém f (c) = 0, patří alespoň jeden bod „c“.
V tomto případě lze hodnotu „c“ snadno vypočítat takto:
Xdva - 2 = 0
x = ± √2.
√2 ≈ 1,4 tedy patří do intervalu [1,2] a splňuje to f (√2) = 0.
Cvičení 2
Ukažte, že rovnice x5 + x + 1 = 0 má alespoň jedno skutečné řešení.
Řešení
Nejprve si všimněme, že f (x) = x5 + x + 1 je polynomiální funkce, což znamená, že je spojitá na všech reálných číslech.
V tomto případě není uveden žádný interval, proto je nutné hodnoty vyhodnotit intuitivně, nejlépe blízko 0, aby bylo možné vyhodnotit funkci a najít změny znaménka:
Pokud použijete interval [0, 1], musíte:
f (x) = x5 + x + 1.
f (0) = 05 + 0 + 1 = 1> 0.
f (1) = 15 + 1 + 1 = 3> 0.
Protože nedochází ke změně znaménka, proces se opakuje s dalším intervalem.
Pokud použijete interval [-1, 0], musíte:
f (x) = x5 + x + 1.
f (-1) = (-1)5 + (-1) + 1 = -1 < 0.
f (0) = 05 + 0 + 1 = 1> 0.
V tomto intervalu dochází ke změně znaménka: znaménko f (-1) ≠ znaménko f (0), což znamená, že funkce f (x) = x5 + x + 1 má v intervalu [-1, 0] alespoň jeden skutečný kořen „c“, takže f (c) = 0. Jinými slovy platí, že x5 + x + 1 = 0 má skutečné řešení v intervalu [-1,0].
Reference
- Bronshtein I, S. K. (1988). Matematický manuál pro inženýry a studenty… Redakční MIR.
- George, A. (1994). Matematika a mysl. Oxford University Press.
- Ilín V, P. E. (1991). Matematická analýza. Ve třech svazcích ...
- Jesús Gómez, F. G. (2003). Učitelé středních škol. Svazek II. ŠÍLENÝ.
- Mateos, M. L. (2013). Základní vlastnosti analýzy v R. Editores, 20. prosince.
- Piskunov, N. (1980). Diferenciální a integrální počet ...
- Sydsaeter K, H. P. (2005). Matematika pro ekonomickou analýzu. Felix Varela.
- William H. Barker, R. H. (s.f.). Kontinuální symetrie: Od Euklida po Kleina. American Mathematical Soc.


Zatím žádné komentáře