
Čebyšovova věta, co to je, aplikace a příklady
The Čebyšovova věta (nebo Čebyšovova nerovnost) je jedním z nejdůležitějších klasických výsledků teorie pravděpodobnosti. Umožňuje odhadnout pravděpodobnost události popsané pomocí náhodné proměnné X tím, že nám poskytne vazbu, která nezávisí na distribuci náhodné proměnné, ale na rozptylu X.
Věta je pojmenována po ruském matematikovi Pafnuty Chebyshovovi (psaném také jako Čebyčev nebo Tchebycheff), který, i když nebyl první, kdo uvedl teorém, jako první vydal důkaz v roce 1867.

Tato nerovnost, nebo ty, které se kvůli jejich vlastnostem nazývají Chebyshovova nerovnost, se používá hlavně k aproximaci pravděpodobností výpočtem hranic.
Rejstřík článků
- 1 Co dělá?
- 2 Aplikace a příklady
- 2.1 Omezení pravděpodobností
- 2.2 Důkaz o limitních větách
- 2.3 Velikost vzorku
- 3 Nerovnosti typu Čebyšov
- 4 Odkazy
Z čeho se skládá?
Při studiu teorie pravděpodobnosti se stává, že pokud je známa distribuční funkce náhodné proměnné X, lze vypočítat její očekávanou hodnotu nebo matematické očekávání E (X) - a její rozptyl Var (X), pokud takové množství existuje . Konverzace však nemusí být nutně pravdivá..
To znamená, že když známe E (X) a Var (X), není nutně možné získat distribuční funkci X, proto je velmi obtížné získat veličiny jako P (| X |> k) pro některá k> 0. Ale díky Čebyšovově nerovnosti je možné odhadnout pravděpodobnost náhodné proměnné.
Čebyšovova věta nám říká, že pokud máme náhodnou proměnnou X nad prostorem vzorku S s pravděpodobnostní funkcí p, a pokud k> 0, pak:
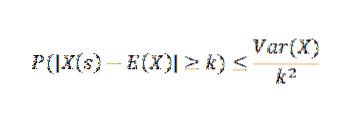
Aplikace a příklady
Z mnoha aplikací Čebyšovovy věty lze zmínit následující:
Omezení pravděpodobností
Toto je nejběžnější aplikace a používá se k určení horní hranice pro P (| X-E (X) | ≥k), kde k> 0, pouze s rozptylem a očekáváním náhodné proměnné X, bez znalosti pravděpodobnostní funkce.
Příklad 1
Předpokládejme, že počet produktů vyrobených ve společnosti během týdne je náhodná proměnná s průměrem 50.
Pokud je známo, že rozptyl týdne výroby se rovná 25, co můžeme říci o pravděpodobnosti, že tento týden se produkce bude lišit o více než 10 od průměru?
Řešení
Aplikujeme Čebyšovovu nerovnost a máme:
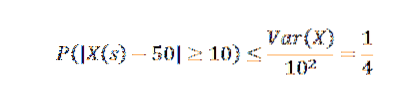
Z toho můžeme získat, že pravděpodobnost, že v týdnu výroby počet článků přesáhne průměr o více než 10, je maximálně 1/4.
Důkaz o limitních větách
Čebyšovova nerovnost hraje důležitou roli při dokazování nejdůležitějších limitních vět. Jako příklad máme následující:
Slabý zákon velkého počtu
Tento zákon stanoví, že vzhledem k posloupnosti X1, X2,…, Xn,… nezávislých náhodných proměnných se stejným průměrným rozdělením E (Xi) = μ a odchylkou Var (X) = σdva, a známý průměrný vzorek:
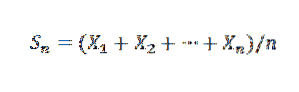
Pak pro k> 0 máme:
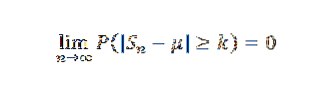
Nebo ekvivalentně:
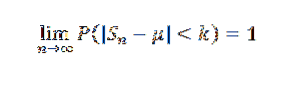
Demonstrace
Nejprve si všimněte následujícího:
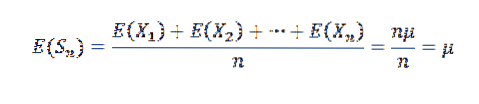
Protože X1, X2,…, Xn jsou nezávislé, vyplývá z toho, že:
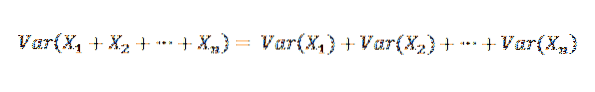
Proto je možné uvést následující:
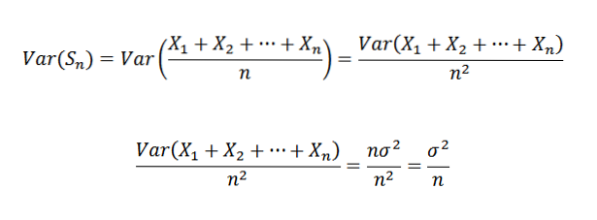
Pak pomocí Čebyšovovy věty máme:
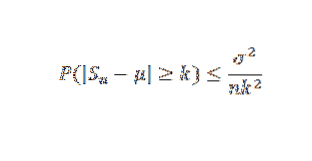
Nakonec věta vyplývá ze skutečnosti, že limit vpravo je nula, když n má sklon k nekonečnu.
Je třeba poznamenat, že tento test byl proveden pouze pro případ, kdy existuje rozptyl Xi; to znamená, že se nerozchází. Pozorujeme tedy, že věta vždy platí, pokud existuje E (Xi).
Čebyšovova limitní věta
Pokud X1, X2,…, Xn,… je posloupnost nezávislých náhodných proměnných tak, že existuje nějaká C< infinito, tal que Var(Xn) ≤ C para todo n natural, entonces para cualquier k>0:
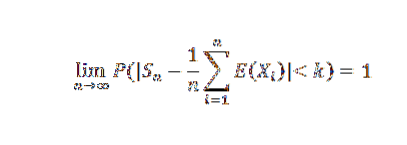
Demonstrace
Protože posloupnost odchylek je rovnoměrně ohraničená, máme pro všechny přirozené n Var (Sn) ≤ C / n. Ale víme, že:
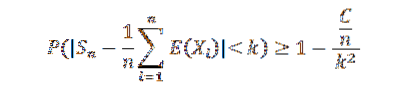
Díky tomu, že n má sklon k nekonečnu, mají následující výsledky:
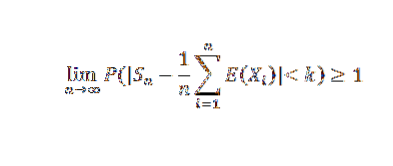
Protože pravděpodobnost nemůže překročit hodnotu 1, získá se požadovaný výsledek. V důsledku této věty bychom mohli zmínit konkrétní případ Bernoulliho.
Pokud se experiment opakuje nkrát nezávisle se dvěma možnými výsledky (selhání a úspěch), kde p je pravděpodobnost úspěchu v každém experimentu a X je náhodná proměnná, která představuje počet získaných úspěchů, pak pro každé k> 0 máte na:
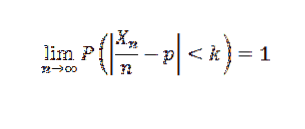
Velikost vzorku
Pokud jde o rozptyl, Čebyšovova nerovnost nám umožňuje najít velikost vzorku n, která je dostatečná k zajištění toho, že pravděpodobnost výskytu | Sn-μ |> = k je tak malá, jak je požadováno, což nám umožňuje aproximaci k průměrný.
Přesně, nechť X1, X2,… Xn je vzorek nezávislých náhodných proměnných velikosti n a předpokládejme, že E (Xi) = μ a jeho rozptyl σdva. Čebyšovovou nerovností tedy máme:
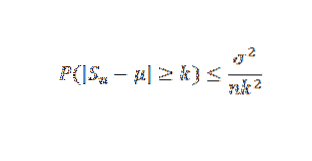
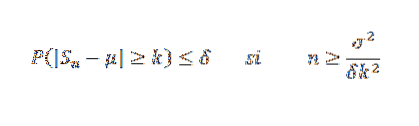
Příklad
Předpokládejme, že X1, X2,… Xn jsou vzorky nezávislých náhodných proměnných s Bernoulliho distribucí, takže berou hodnotu 1 s pravděpodobností p = 0,5.
Jaká by měla být velikost vzorku, aby bylo možné zaručit, že pravděpodobnost, že rozdíl mezi aritmetickým průměrem Sn a jeho očekávanou hodnotou (přesahující o více než 0,1), je menší nebo roven 0,01?
Řešení
Máme E (X) = μ = p = 0,5 a Var (X) = σdva= p (1-p) = 0,25. Podle Čejshovovy nerovnosti pro libovolné k> 0 máme:
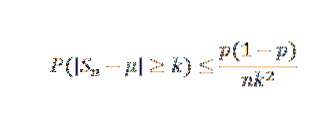
Nyní, když vezmeme k = 0,1 a δ = 0,01, máme:
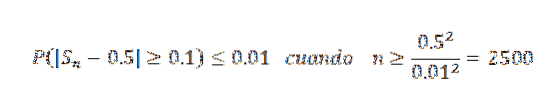
Tímto způsobem se dospělo k závěru, že je potřeba velikost vzorku nejméně 2 500, aby se zajistilo, že pravděpodobnost události | Sn - 0,5 |> = 0,1 je menší než 0,01.
Nerovnosti typu Čebyšov
S Čebyšovovou nerovností souvisí několik nerovností. Jednou z nejznámějších je Markovova nerovnost:
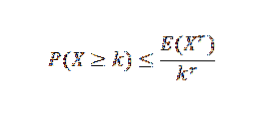
V tomto výrazu X je nezáporná náhodná proměnná s k, r> 0.
Markovova nerovnost může mít různé podoby. Například nechť Y je nezáporná náhodná proměnná (takže P (Y> = 0) = 1) a předpokládejme, že E (Y) = μ existuje. Předpokládejme také, že (E (Y))r= μr existuje pro celé číslo r> 1. Pak:
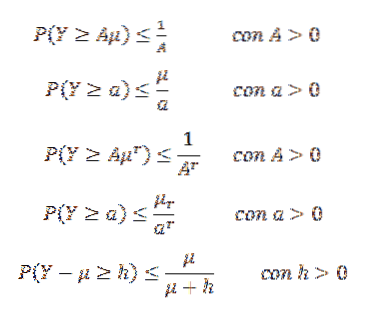
Další nerovnost je Gaussian, která nám říká, že vzhledem k unimodální náhodné proměnné X s režimem na nule, pak pro k> 0,
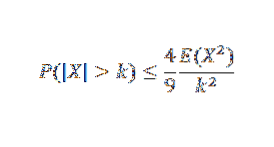
Reference
- Kai Lai Chung. Teorie základní stability se stochastickými procesy. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskrétní matematika a její aplikace. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Pravděpodobnost a statistické aplikace. S.A. MEXICKÁ ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Vyřešené problémy diskrétní matematiky. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teorie a pravděpodobnostní problémy. McGRAW-HILL.



Zatím žádné komentáře