
Vysvětlení věty o superpozici, aplikace, řešená cvičení
The věta o superpozici, V elektrických obvodech zjišťuje, že napětí mezi dvěma body nebo proud, který jimi prochází, je algebraickým součtem napětí (nebo proudů, je-li tomu tak) v důsledku každého zdroje, jako by každý z nich působil jiným způsobem Nezávislý.
Tato věta nám umožňuje analyzovat lineární obvody, které obsahují více než jeden nezávislý zdroj, protože je nutné vypočítat pouze příspěvek každého z nich zvlášť..

Pro uplatnění věty je rozhodující lineární závislost. Lineární obvod je obvod, jehož odezva je přímo úměrná vstupu.
Například Ohmův zákon aplikovaný na elektrický odpor to říká V = i.R., kde PROTI je napětí, R je odpor e i je aktuální. Jedná se pak o lineární závislost napětí a proudu v odporu.
V lineárních obvodech se uplatňuje princip superpozice s přihlédnutím k následujícímu:
-Každý nezávislý zdroj napětí musí být zvážen samostatně, a proto je nutné vypnout všechny ostatní. Stačí uvést na 0 V všechny, které nejsou analyzovány, nebo je ve schématu nahradit zkratem.
-Pokud je zdroj aktuální, musíte obvod otevřít.
-Při zvažování vnitřního odporu jak proudových, tak napěťových zdrojů musí zůstat na svém místě a tvoří součást zbytku obvodu..
-Pokud existují závislé zdroje, musí zůstat tak, jak vypadají v obvodu.
Rejstřík článků
- 1 Aplikace
- 2 kroky k použití věty o superpozici
- 3 Vyřešená cvičení
- 3.1 - Příklad 1
- 3.2 - Cvičení 2
- 4 Odkazy
Aplikace
Věta o superpozici se používá k získání jednodušších a snáze zpracovatelných obvodů. Vždy je však třeba mít na paměti, že se vztahuje pouze na osoby s lineární odezvou, jak bylo řečeno na začátku.
Nelze jej tedy použít například přímo k výpočtu výkonu, protože výkon souvisí s proudem pomocí:
P = idva R
Jelikož je proud na druhou, není odezva lineární. Rovněž neplatí pro magnetické obvody zahrnující transformátory..
Na druhou stranu věta o superpozici nabízí příležitost poznat účinek, který má každý zdroj na obvod. A samozřejmě, prostřednictvím jeho aplikace je možné to vyřešit úplně, to znamená znát proudy a napětí přes každý odpor.
Věta o superpozici může být také použita ve spojení s jinými větami o obvodu, například Théveninovými, k řešení složitějších konfigurací..
V obvodech se střídavým proudem je věta také užitečná. V tomto případě pracujeme s impedancemi místo s rezistory, pokud lze celkovou odezvu každé frekvence vypočítat samostatně..
A konečně, v elektronických systémech je věta použitelná pro analýzu stejnosměrného i střídavého proudu, samostatně.
Kroky k použití věty o superpozici
-Deaktivujte všechny nezávislé zdroje podle pokynů uvedených na začátku, kromě těch, které mají být analyzovány.
-Určete výstup, buď napětí, nebo proud, který tento jediný zdroj produkuje.
-Opakujte dva kroky popsané pro všechny ostatní zdroje.
-Vypočítejte algebraický součet všech příspěvků nalezených v předchozích krocích.
Vyřešená cvičení
Níže zpracované příklady objasňují použití věty v některých jednoduchých obvodech.
- Příklad 1
V obvodu zobrazeném na následujícím obrázku najděte proud přes každý odpor pomocí věty o superpozici.
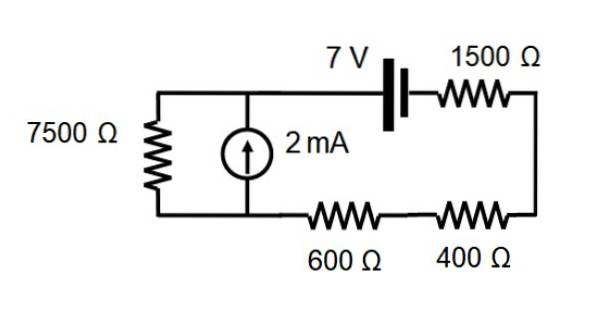
Řešení
Příspěvek zdroje napětí
Za prvé, zdroj proudu je vyloučen, což způsobí, že obvod bude vypadat takto:

Ekvivalentní odpor se zjistí sečtením hodnoty každého odporu, protože jsou všechny v sérii:
7500 +600 +400 + 1500 Ω = 10 000 Ω
Uplatňování Ohmova zákona V = I.R. a vymazání proudu:
I = V / R = 7/10 000 A = 0,0007 A = 0,7 mA
Tento proud je stejný pro všechny rezistory.
Příspěvek aktuálního zdroje
Zdroj napětí je okamžitě odstraněn, aby fungoval pouze se zdrojem proudu. Výsledný obvod je uveden níže:
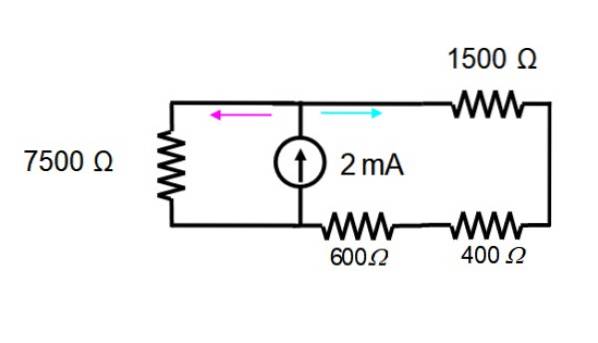
Rezistory na obrazovce vpravo jsou v sérii a lze je nahradit jedním:
600 +400 + 1500 Ω = 2500 Ω
Výsledný obvod vypadá takto:
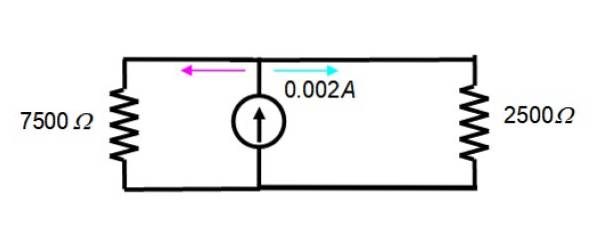
Proud 2 mA = 0,002 A je rozdělen mezi dva odpory na obrázku, proto platí rovnice děliče proudu:
JáX = (R.ekv/ R.X) JáT
Kde JáX je proud v rezistoru RX, Rekv symbolizuje ekvivalentní odpor e JáT je celkový proud. Je nutné najít ekvivalentní odpor mezi oběma, s vědomím, že:
1 / R.ekv = (1 / R.1) + (1 / R.dva)
Proto:
1 / R.ekv = (1/7500) + (1/2500) = 1/1875 → R.ekv = 1875 Ω
U tohoto druhého obvodu je proud přes odpor 7500 Ω nalezen dosazením hodnot do rovnice děliče proudu:
Já7500 Ω = (1875/7500). 0,002 A = 0,0005 A = 0,5 mA
Zatímco ten, který prochází rezistorem 2500 Ω, je:
Já2500 Ω = 2 mA - 0,5 mA = 1,5 mA
Aplikace věty o superpozici
Nyní je pro každý odpor použita věta o superpozici, počínaje 400 Ω:
Já400 Ω = 1,5 mA - 0,7 mA = 0,8 mA
Důležité: pro tento odpor, proudy jsou odečteny, jak obíhají v opačném směru, podle pečlivého pozorování čísel, kde směry proudů mají různé barvy.
Stejný proud prochází rezistory 1500 Ω a 600 Ω stejně, protože jsou všechny v sérii.
Věta se poté použije k nalezení proudu přes rezistor 7500 Ω:
Já7500 Ω = 0,7 mA + 0,5 mA = 1,2 mA
Důležité: v případě rezistoru 7500 Ω si povšimněte proudy se sčítají, protože v obou obvodech při průchodu tímto odporem cirkulují stejným směrem. Opět je nutné pečlivě sledovat směry proudů.
- Cvičení 2
Nalezení proudu a napětí na 12 Ω rezistoru pomocí věty o superpozici.
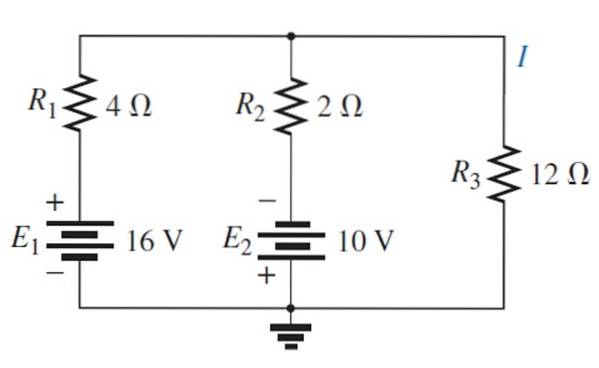
Řešení
Písmo E je nahrazeno1 se zkratem:
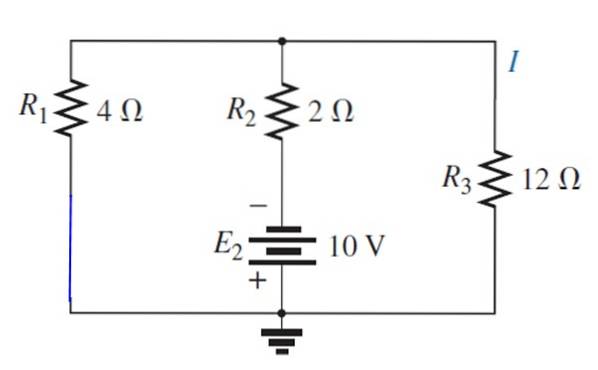
Výsledný obvod je nakreslen následovně, aby bylo možné snadno vizualizovat odpory, které zůstávají paralelně:
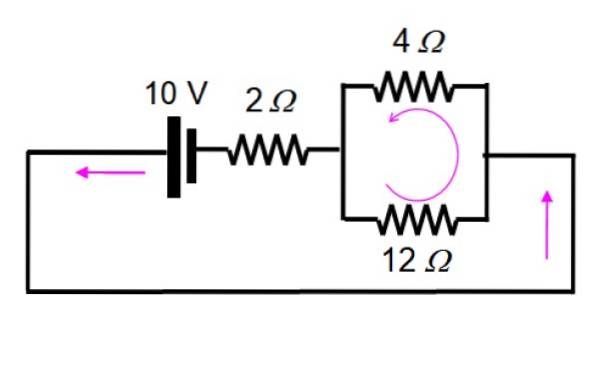
A teď je to vyřešeno použitím řady a paralelně:
1 / R.ekv = (1/12) + (1/4) = 1/3 → R.ekv = 3 Ω
Tento odpor je zase v sérii s odporem 2 Ω, proto je celkový odpor 5 Ω. Celkový proud je:
I = V / R = 10 V / 5 Ω = 2 A
Tento stream je rozdělen jako:
Já12 Ω = (3/12) 2 A = 0,5 A
Proto je napětí:
PROTI12 Ω = 0,5 A × 12 Ω = 6 V
Nyní je aktivován zdroj E.1:
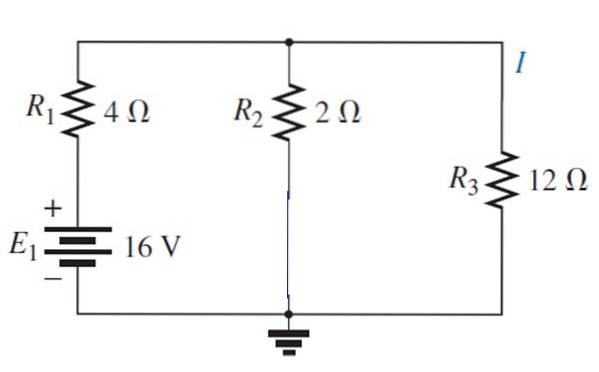
Výsledný obvod lze nakreslit takto:

1 / R.ekv = (1/12) + (1/2) = 7/12 → Rekv = 12/7 Ω
A v sérii s tím 4 Ω výsledkem je ekvivalentní odpor 40/7 Ω. V tomto případě je celkový proud:
I = V / R = 16 V / (40/7) Ω = 14/5 A
Rozdělovač napětí se znovu použije s těmito hodnotami:
Já12Ω = ((12/7) / 12) (14/5) A = 0,4 A
Výsledný proud je: 0,5 - 0,4 A = 0,1 A. Všimněte si, že byly odečteny, protože proud z každého zdroje má jiný smysl, jak je vidět v původním obvodu.
Napětí na rezistoru je:
PROTI12 Ω = 0,4 A × 12 Ω = 4,8 V
Nakonec je celkové napětí: 6V-4,8V = 1,2V
Reference
- Alexander, C. 2006. Základy elektrických obvodů. 3. místo Edice. Mc Graw Hill.
- Boylestad, R. 2011. Úvod do analýzy obvodů. 2. místo Edice. Pearson.
- Dorf, R. 2006. Úvod do elektrických obvodů. 7. Edice. John Wiley & Sons.
- Edminister, J. 1996. Elektrické obvody. Série Schaum. 3. místo Edice. Mc Graw Hill
- Wikipedia. Aktuální dělič. Obnoveno z: es.wikipedia.org.


Zatím žádné komentáře