
Charakteristika vodorovného záběru, vzorce a rovnice, cvičení
The horizontální záběr Jedná se o vystřelení střely s horizontální rychlostí z určité výšky a ponechané gravitační akci. Bez ohledu na odpor vzduchu bude mít dráha popsaná mobilem tvar parabolového oblouku.
Horizontální promítání objektů je zcela běžné. Střely jsou vypouštěny pro všechny druhy účelů: od kamenů, kterými byly na začátku příběhu zasaženy přehrady, až po ty, které se provádějí v míčových sportech, a jsou těsně sledovány davy.
Rejstřík článků
- 1 Funkce
- 2 Vzorce a rovnice
- 2.1 Poloha, rychlost, doba letu a maximální horizontální dosah
- 3 Vyřešená cvičení
- 3.1 - Cvičení vyřešeno 1
- 3.2 - Vyřešené cvičení 2
- 4 Odkazy
Vlastnosti
Hlavní charakteristiky horizontálního záběru jsou:
-Počáteční rychlost daná střele je kolmá na gravitaci.
-Pohyb probíhá v rovině, takže trvá dvě souřadnice: X Y Y.
-Dělá se to od určité výšky H nad úrovní terénu.
-Doba, po kterou projektil vydrží ve vzduchu, se nazývá doba letu.
-Faktory, jako je odpor vzduchu a kolísání hodnoty G.
-Tvar, velikost a hmotnost střely neovlivňují její pohyb.
-Pohyb se rozloží na dva současné pohyby: jeden svisle dolů při působení G; druhý, vodorovný, s konstantní rychlostí.
Vzorce a rovnice
Kinematické rovnice pro vodorovný start jsou získány z rovnic pro volný pád a rovnic pro rovnoměrný přímočarý pohyb..
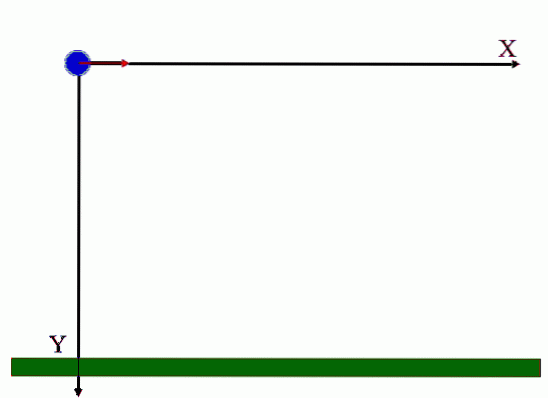
Jak jasně ukazuje animace na obrázku 1, dostává projektil vodorovnou počáteční rychlost označenou jako protinebo = vvůl i (tučně v tištěném textu označuje, že se jedná o vektor).
Všimněte si, že počáteční rychlost má velikost protivůl a je směrován podél osy X, jaký je směr jednotkového vektoru i. Animace také ukazuje, že počáteční rychlost nemá svislou složku, ale jak klesá, tato složka se rovnoměrně zvyšuje díky akci G, gravitační zrychlení.
Pokud jde o horizontální složku rychlosti, zůstává po celou dobu pohybu konstantní.
Podle výše uvedeného jsou polohy stanoveny jako funkce času, a to jak na vodorovné ose, tak na svislé ose. Směr doprava je brán jako osa + x, zatímco směr dolů je směr -y. Hodnota gravitace je g = -9,8 m / sdva nebo -32 ft / sdva:
x (t) = xnebo + protivůl.t (Horizontální poloha); protivůl je to konstantní
y (t) = ynebo + protiAhoj.t - ½ g.t.dva (svislá poloha); protiY = vAhoj - g.t (vertikální rychlost)
Poloha, rychlost, doba letu a maximální horizontální dosah
Rovnice se zjednodušují výběrem následujících výchozích pozic: Xnebo = 0, Ynebo = 0 na místě spuštění. Co víc protiAhoj = 0, protože mobilní telefon je promítán vodorovně. S touto volbou jsou pohybové rovnice následující:
x (t) = vvůl.t; protiX = vvůl
y (t) = - ½ g.t.dva; protiY = - g.t.
Pokud není čas k dispozici, je užitečná rovnice vztahující se k rychlostem a posunům. To platí pro vertikální rychlost, protože horizontální zůstává během pohybu konstantní:
protiYdva = vAhojdva + 2.g .y = 2.g.y.
Doba letu
Pro výpočet doba letu tlet, Předpokládejme, že je mobil promítán z výšky H na podlaze. Vzhledem k tomu, že původ referenčního systému byl zvolen v místě spuštění, je při dosažení země v poloze -H. Dosazením do rovnice 2) dostaneme:
-H = - ½ g.t.dvalet
tlet = (2H / g)½
Maximální dosah
The horizontální dosah se získá dosazením tentokrát do x (t):
Xmax = vvůl. (2H / g)½
Vyřešená cvičení
-Vyřešené cvičení 1
Vrtulník letí vodorovně a udržuje si konstantní převýšení 580 m, když přes uprchlický tábor odhodí krabici s jídlem. Krabice přistává ve vodorovné vzdálenosti 150 m od bodu jejího spuštění. Najít: a) Čas letu boxu.
b) Rychlost vrtulníku.
c) Jak rychle se krabice dotkla země??
Řešení
a) Výška H, ze které je jídlo upuštěno, je H = 500 m. S těmito údaji při nahrazování získáme:
tlet = (2H / g)½= (2 x 580 / 9,8) ½s = 10,9 s
b) Vrtulník nese počáteční vodorovnou rychlost protivůl balíčku a protože jeden z údajů je Xmax:
Xmax = vvůl. (2H / g)½ ® protivůl = xmax / (2H / g)½= xmax / tlet = 150 m / 10,9 s = 13,8 m / s
c) Rychlost střely v kterémkoli okamžiku je:
protiY = -g.t = -9,8 m / sdva x 10,9 s = -106,82 m / s = - 384,6 km / h
Záporné znaménko znamená, že se mobil pohybuje dolů.
-Cvičení vyřešeno 2
Z letadla letícího vodorovně ve výšce H = 500 m Y 200 km / h balíček spadne a musí spadnout na otevřené vozidlo, které jede 18 km / h na cestě. V jaké poloze musí letadlo spadnout balíček tak, aby spadl do vozidla? Nezohledňujte odpor vzduchu ani rychlost větru.
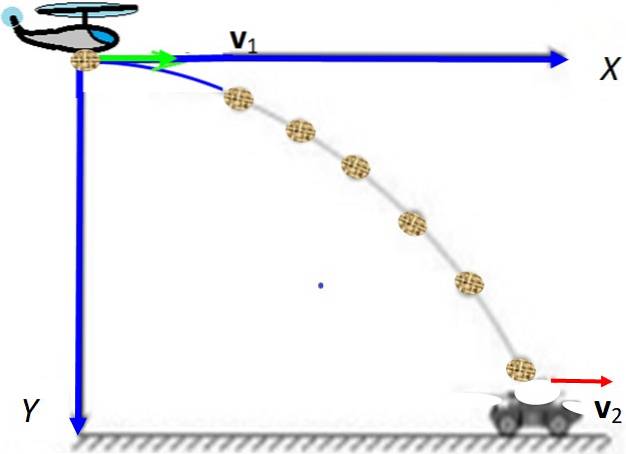
Řešení
Je vhodné nejprve předat všechny jednotky do mezinárodního systému:
18 km / h = 6 m / s
200 km / h = 55 m / s
Existují dva mobilní telefony: letadlo (1) a vozidlo (2) a je nutné zvolit souřadný systém, který oba umístí. Je vhodné to udělat v počátečním bodě balíčku v letadle. Balíček se promítá vodorovně s rychlostí, kterou letadlo nese: proti1, zatímco se vozidlo pohybuje protidva předpokládaná konstanta.
-Letoun
Počáteční pozice: x = 0; y = 0
Počáteční rychlost = proti1 (horizontální)
Polohové rovnice: y (t) = -½g.tdva ; x (t) = v1.t
-Vozidlo
Počáteční pozice: x = 0, y = -H
Počáteční rychlost = protidva (konstantní)
x (t) = xnebo + protidva. t
Doba letu balíčku je:
tlet = (2H / g)½ = (2 × 500 / 9,8)½s = 10,1 s
V této době došlo u balíčku k horizontálnímu posunutí:
Xmax = vvůl . (2H / g)½= 55 m / s x 10,1 s = 556 m.
V této době se vozidlo pohybovalo také vodorovně:
x (t) = v1.t = 6 m / s x10,1 s = 60,6 m
Pokud letadlo odhodí balíček okamžitě, když vidí, že pod ním prochází vozidlo, nedovolí mu spadnout přímo do něj. Aby se to stalo, musíte to vrátit zpět:
d = 556 m - 60,6 m = 495,4 m.
Reference
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill. 74-84.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 1. Kinematika. Upravil Douglas Figueroa (USB). 117 - 164.
- Pohyb střely. Obnoveno z: phys.libretexts.org.
- Rex, A. 2011. Základy fyziky. Pearson. 53-58.
- Tippens, P. 2011. Fyzika: koncepty a aplikace. 7. vydání. McGraw Hill. 126-131.


Zatím žádné komentáře