
Formule práce, jednotky, příklady, cvičení

The práce Ve fyzice se jedná o přenos energie prováděný silou, když se pohybuje předmět, na který působí. Matematicky má podobu skalárního součinu mezi silovými vektory F a posunutí s.
A protože skalární součin mezi dvěma kolmými vektory je nulový, stává se, že síly, které tvoří 90 ° s posunem, nefungují podle definice, protože:
W = F ● s = F⋅ s⋅ cos θ
Kde W označuje práci, z anglického slova práce.
Výhodou definice díla je, že je skalární, to znamená, že nemá směr ani smysl, pouze modul a příslušnou jednotku. To usnadňuje provádění výpočtů zahrnujících energetické změny způsobené působením sil..
Gravitace a kinetické tření jsou příklady sil, které často pracují na pohybujících se objektech. Další společná síla je normální síla vyvíjená povrchem, ale na rozdíl od těchto nikdy nepůsobí na objekty, protože je kolmá na posunutí..
Když tělo volně padá, gravitace vykonává na mobilu pozitivní práci, což způsobuje, že při pádu zvyšuje svou rychlost. Na druhou stranu má kinetické tření zcela opačný účinek, protože vždy, když se staví proti pohybu, vykonává negativní práci, která mu není nakloněna..
Rejstřík článků
- 1 Vzorce a konkrétní případy
- 1.1 Práce prováděná proměnnými silami
- 2 pracovní jednotky
- 2.1 Jednotky v britském systému
- 2.2 Ostatní pracovní jednotky
- 3 Příklady práce
- 3.1 Výstup a sestup předmětů
- 3.2 Bodové náboje v elektrických polích
- 3.3 Tření mezi povrchy
- 3.4 Zatlačte a zatáhněte
- 3.5 Síla v kladce
- 3.6 Normální síly nebo podpory
- 3.7 Magnetická síla
- 3.8 Předměty vázané na laně
- 3.9 Družice na oběžné dráze
- 3.10 Systém hmotnostních pružin
- 4 Cvičení vyřešeno
- 5 Reference
Vzorce a konkrétní případy
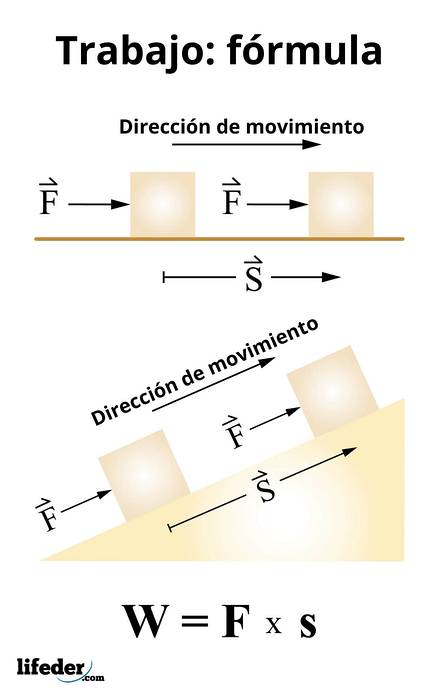
Práce se počítá podle:
W = F ● s
Tento výraz platí pro konstantní síly a podle definice skalárního součinu je ekvivalentní:
W = F. s. cos θ
Kde θ je úhel mezi silou a posunem. Z toho tedy vyplývá, že na těle mohou pracovat pouze ty síly, které mají složku ve směru posunutí.
A také je jasné, že pokud nedojde k žádnému pohybu, nebude ani práce.
Pokud jde o znaménko, práce může být kladná, záporná nebo nulová. V případě, že síla má složku rovnoběžnou s pohybem, závisí znaménko práce na hodnotě cos θ.
Existují některé konkrétní případy, které stojí za zvážení:
- Když je síla rovnoběžná s posunem, úhel mezi F Y s je 0 °, proto je práce vykonaná silou kladná a její hodnota je maximální:
W = F⋅s cos 0º = F⋅s
- Pokud síla působí proti posunutí, pak úhel mezi F Y s je 180 °, práce F je negativní a je minimální:
W = F⋅s cos 180º = -F⋅s
- Nakonec je zde případ zmíněný dříve: pokud úhel tvoří F Y s je 90 °, protože cos 90 ° = 0, práce má hodnotu null:
W = F⋅s cos 90º = 0
Práce prováděná proměnnými silami
Někdy použitá síla není konstantní; v takovém případě se musíte uchýlit k výpočtu, abyste našli práci. Nejprve je určen pracovní rozdíl dW, provedený na nekonečně malém posunutí ds:
dW = F⋅ds
Chcete-li zjistit hodnotu celkové práce odvedené touto silou, když objekt prochází z bodu A do bodu B, je nutné integrovat obě strany, například takto:
Pracovní jednotky
Jednotkou pro práci v mezinárodním systému je joule, zkráceně J. Jednotka je pojmenována podle anglického fyzika Jamese Prescotta Joule, průkopníka ve studiu termodynamiky..
Z pracovní rovnice je joule definován jako 1 newton na metr:
1 J = 1 N⋅m
Jednotky v britském systému
Práce odpovídá jednotce libra síla x noha, někdy zavolat libra-síla nohy. Je to také jednotka energie, ale je třeba si uvědomit, že práce prováděná na těle mění jeho energetický stav, a proto jsou práce a energie rovnocenné. Není divu, že mají stejné disky.
Ekvivalence mezi nohou síly libry a joulem je následující:
1 stopa-libra síla = 1,35582 J
Známou jednotkou pro práci a energii, zejména pro oblast chlazení a klimatizace, je BTU nebo Britská tepelná jednotka.
1 BTU se rovná 1055 J a síle 778,169 nohy-libra.
Ostatní jednotky pro práci
Existují další jednotky pro práci, které se používají ve specifických oblastech fyziky a techniky. Mezi nimi máme:
Erg
Označeno jako erg, je jednotka práce v cegesimálním systému a rovná se 1 dyna⋅cm nebo 1 x 10-7 J.
Elektronový volt
Zkráceně eV se běžně používá ve fyzice částic a je definována jako energie, kterou elektron získá, když se pohybuje potenciálním rozdílem 1 V.
Kilowatthodina (kWh)
Často se objevuje na účtech. Jedná se o práci prováděnou po dobu 1 hodiny zdrojem, jehož výkon je 1 kW, což odpovídá 3,6 x 106 J.
Kalorie
Obvykle to souvisí s energií potravin, i když ve skutečnosti se v této souvislosti odkazuje na a kilokalorie, tj. 1000 kalorií. Ve skutečnosti existuje několik jednotek, které dostávají tento název, takže kontext musí být specifikován velmi dobře.
Rovnocennost mezi joulem a 1 termochemická kalorie to je:
1 kalorie = 4,1840 J
Pracovní příklady
Stoupání a klesání předmětů
Když těla klesají svisle nebo dolů po rampě, váha dělá pozitivní práci a upřednostňuje pohyb. Místo toho, kdykoli objekt stoupá, gravitace působí negativně.
Bodové náboje v elektrických polích
Jednotné elektrické pole funguje na bodovém náboji pohybujícím se uvnitř. V závislosti na poli a znaménku náboje může být tato práce negativní nebo pozitivní.
Tření mezi povrchy
Kinetické tření mezi povrchy vždy působí negativně na pohybující se objekt.
Tlačit a táhnout

Tlačení je síla, která odtahuje předmět od něčeho. Tahání je síla, díky níž se objekt přibližuje.
Síla v kladce
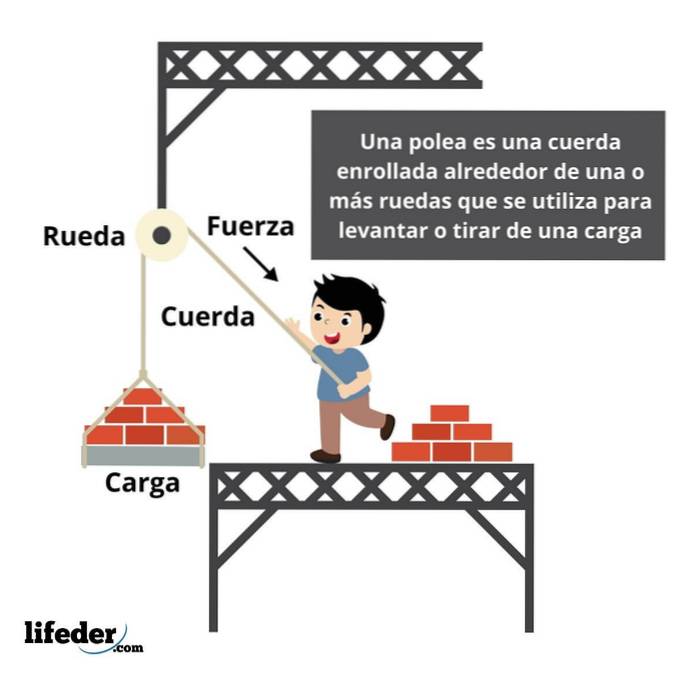
Kladka je systém používaný k přenosu síly z jednoho z jejích konců. U jednoduché kladky musí být za účelem zvednutí břemena použita síla rovnající se odporu vyvíjenému předmětem.
Normální síly nebo podpory
Normál, jak je uvedeno výše, funguje nulově, když se na něm pohybuje předmět spočívající na povrchu, i když povrch není plochý nebo je nakloněný..
Magnetická síla
Další silou, která vykonává nulovou práci, je magnetická síla, která vyvíjí jednotné pole na nabitou částici, které je na ni kolmé. Pohyb částice se ukázal být rovnoměrným kruhovým pohybem se silou v radiálním směru. Protože posunutí je kolmé na sílu, nepracuje na zatížení..
Předměty vázané na laně
Lano také nefunguje na zavěšeném kyvadle, protože jeho napětí je vždy kolmé na posunutí hmoty..
Družice na oběžné dráze
Gravitace také nefunguje na satelitu na kruhové oběžné dráze, ze stejného důvodu jako v předchozích případech: je kolmá na posunutí..
Systém hromadné pružiny
V systému hmota-pružina síla F že pružina působí na hmotu, má velikost F = kx, kde k je pružinová konstanta a X jeho stlačení nebo prodloužení. Jde o proměnnou sílu, proto její práce závisí na tom, jak moc se pružina natahuje nebo zmenšuje.
Cvičení vyřešeno
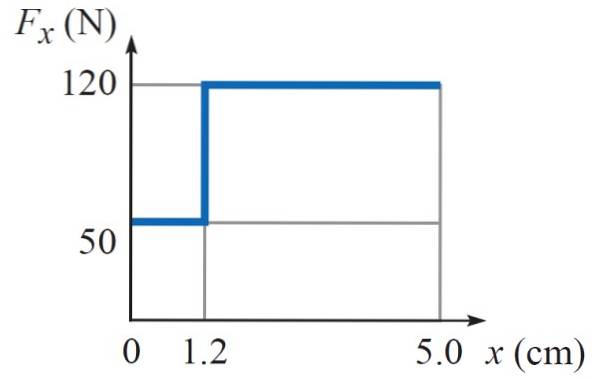
Následující graf ukazuje práci vykonanou proměnnou silou FX což závisí na poloze X. To je síla vyvíjená kladivem na hřebík. První část je síla použitá k přibití na měkčí část stěny a druhá k dokončení zatloukání hřebu.
Kolik práce musí kladivo udělat, aby hřebík zapustil celkem 5 cm do zdi?
Řešení
Síla vyvíjená kladivem je proměnlivá, protože k zatlačení hřebíku 1,2 cm do měkké části stěny je zapotřebí menší intenzita (50 N), zatímco v tvrdší části je potřeba 120 N, aby se hřebík ponořil na 5 cm hluboko, jak ukazuje graf.
V tomto případě je práce integrálem:

Kde A = 0 cm a B = 5 cm. Protože integrálem je oblast pod grafem Fx vs x, stačí najít tuto oblast, která odpovídá dvěma obdélníkům, první s výškou 50 N a šířkou 1,2 cm a druhý s výškou 120 N a šířkou (5 cm - 1,2 cm) = 3,8 cm.
Oba jsou vypočítány a přidány, aby poskytly celkovou práci:
Š = 50 N x 1,2 cm + 120 N x 3,8 cm = 516 N. cm = 516 N x 0,01 m = 5,16 J.
Reference
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 2. Dynamika. Upravil Douglas Figueroa (USB).
- Giambattista, A. 2010. Fyzika. 2. místo Ed. McGraw Hill.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vyd. 1. díl Pearson.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7. Ed. Cengage Learning.
- Zapata, F. Mechanické práce. Obnoveno z: francesphysics.blogspot.com.



Zatím žádné komentáře