The mechanické práce Je definována jako změna energetického stavu systému způsobená působením vnějších sil, jako je gravitace nebo tření. Jednotky mechanické práce v mezinárodním systému (SI) jsou newton x metr nebo jouly, zkráceně J.
Matematicky je definován jako skalární součin vektoru síly a vektoru posunutí. Ano F je konstantní síla a l je posunutí, oba vektory, práce W je vyjádřena jako: W = F ● l
Když síla není konstantní, musíme analyzovat práci, která je provedena, když jsou posuny velmi malé nebo rozdílné. V tomto případě, pokud je bod A považován za výchozí bod a B za bod příjezdu, je celková práce získána přidáním všech příspěvků. To odpovídá výpočtu následujícího integrálu:
Variace energie systému = Práce vykonaná vnějšími silami
ΔE = Wext
Když se do systému přidá energie, W> 0 a když se energie odečte W<0. Ahora bien, si ΔE = 0, puede significar que:
-Systém je izolovaný a na něj nepůsobí žádné vnější síly.
-Existují vnější síly, ale neprovádějí práci na systému.
Jelikož se změna energie rovná práci odvedené vnějšími silami, je jednotkou energie SI také joule. To zahrnuje jakýkoli typ energie: kinetickou, potenciální, tepelnou, chemickou a další..
Rejstřík článků
Už jsme viděli, že práce je definována jako bodový produkt. Vezměme si definici práce konstantní síly a aplikujme koncept tečkového součinu mezi dva vektory:
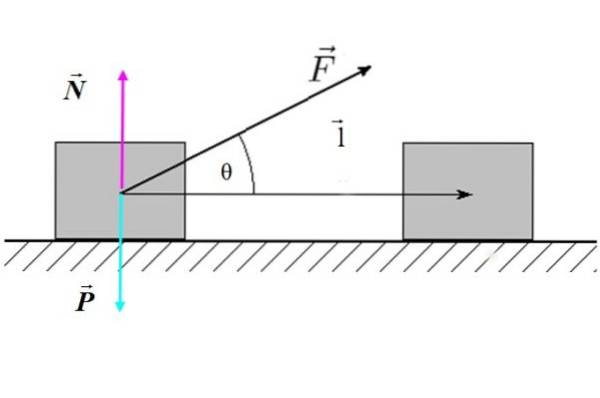
W = F ● l = F.l.cos θ
Kde F je velikost síly, l je velikost posunutí a θ je úhel mezi silou a posunem. Na obrázku 2 je příklad nakloněné vnější síly působící na blok (systém), který vytváří vodorovný posun.
Přepsat dílo následujícím způsobem:
W = (F. cos θ). l
Můžeme konstatovat, že pouze složka síly rovnoběžná s posunem: F. cos θ eje schopen dělat práci. Pokud θ = 90 °, pak cos θ = 0 a práce by byla nulová.
Proto se dospělo k závěru, že síly kolmé na posun neprovádějí mechanickou práci.
V případě obrázku 2 ani normální síla N ani váha P pracujte, protože oba jsou kolmé na posunutí l.
Jak je vysvětleno výše, Ž Může to být pozitivní nebo negativní. Když cos θ> 0, práce vykonaná silou je pozitivní, protože má stejný směr pohybu.
Ano cos θ = 1, síla a posunutí jsou paralelní a práce je maximální.
V případě cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.
Když cos θ = -1, síla je zcela opačná posunutí, jako je kinetické tření, jehož účinkem je zpomalení objektu, na který působí. Práce je tedy minimální.
To souhlasí s tím, co bylo řečeno na začátku: pokud je práce pozitivní, přidává se do systému energie a pokud je negativní, odečítá se.
Čistá práce Žsíť Je definována jako součet práce odvedené všemi silami působícími na systém:
Žsíť = ∑Wi
Pak můžeme dojít k závěru, že k zajištění existence mechanické práce v síti je nutné, aby:
-Vnější síly působí na objekt.
-Tyto síly nejsou všechny kolmé na posunutí (cos θ ≠ 0).
-Úlohy prováděné každou silou se navzájem nevyrušují.
-Došlo k posunutí.
-Kdykoli je nutné uvést předmět do pohybu z klidu, je nutné provést mechanickou práci. Například tlačit ledničku nebo těžký kufr na vodorovný povrch.
-Dalším příkladem situace, kdy musíte provádět mechanické práce, je změna rychlosti pohybujícího se míčku..
-Je třeba pracovat na zvednutí předmětu do určité výšky nad podlahou.
Nyní existují stejně běžné situace, kdy ne práce je hotová, i když zdání naznačuje něco jiného. Řekli jsme, že pro zvednutí předmětu do určité výšky musíte dělat práci, takže předmět přenášíme, zvedáme nad hlavu a držíme ho tam. Děláme práci?
Zdá se, že ano, protože pokud je objekt těžký, paže se v krátké době unaví, ať už je to jakkoli těžké, z hlediska fyziky se nepracuje. Proč ne? Protože se objekt nepohybuje.
Dalším případem, kdy navzdory vnější síle neprovádí mechanickou práci, je situace, kdy má částice jednotný kruhový pohyb.
Například dítě točí kámen uvázaný na provázku. Napětí struny je dostředivá síla, která umožňuje rotaci kamene. Ale tato síla je vždy kolmá na posunutí. Potom neprovádí mechanické práce, i když upřednostňuje pohyb.
Kinetická energie systému je ta, kterou vlastní díky svému pohybu. Ano m je hmotnost a proti je rychlost pohybu, kinetická energie je označena K. a je dána:
K = ½ mvdva
Podle definice nemůže být kinetická energie objektu záporná, protože jak hmotnost, tak druhá mocnina rychlosti jsou vždy kladné veličiny. Kinetická energie může být 0, když je objekt v klidu.
Pro změnu kinetické energie systému je nutné změnit jeho rychlost - budeme uvažovat, že hmotnost zůstává konstantní, i když tomu tak není vždy. To vyžaduje provedení síťové práce v systému, proto:
Žsíť = ΔK.
Toto je věta o práci - kinetické energii. Uvádí, že:
Čistá práce se rovná změně kinetické energie systému
Všimněte si, že i když K je vždy kladné, ΔK může být kladné nebo záporné, protože:
ΔK = K.finále - K. počáteční
Ano K.finále >K. počáteční systém získal energii a ΔK> 0. Naopak, pokud K.finále < K. počáteční, systém se vzdal napájení.
Když je pružina napnutá (nebo stlačená), je třeba pracovat. Tato práce je uložena na jaře, což jí zase umožňuje pracovat například na bloku, který je připevněn k jednomu z jejích konců..
Hookeův zákon stanoví, že síla vyvíjená pružinou je obnovovací silou - je v rozporu s posunem - a také úměrná uvedenému posunutí. Konstanta proporcionality závisí na tom, jak pružina je: měkká a snadno deformovatelná nebo tuhá.
Tato síla je dána:
Fr = -kx
Ve výrazu, Fr je síla, k je pružinová konstanta a X je posunutí. Záporné znaménko označuje, že síla vyvíjená pružinou je proti posunutí.
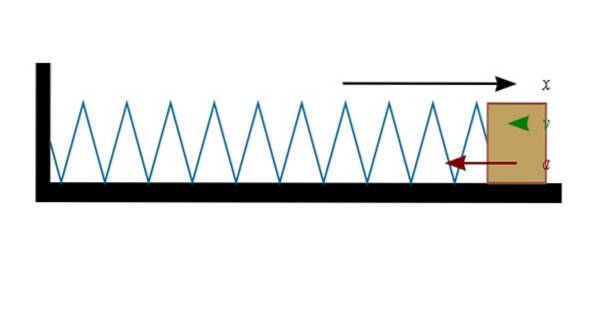
Pokud je pružina stlačena (na obrázku doleva), blok na jejím konci se posune doprava. A když se pružina natáhne (doprava), blok se bude chtít posunout doleva.
Chcete-li stlačit nebo natáhnout pružinu, musí práci provést nějaký externí agent, a protože se jedná o proměnnou sílu, k výpočtu uvedené práce musíme použít definici uvedenou na začátku:
Je velmi důležité si uvědomit, že se jedná o práci externího agenta (například ruky osoby) při stlačování nebo roztažení pružiny. Proto se záporné znaménko neobjevuje. A protože pozice jsou čtvercové, nezáleží na tom, zda se jedná o komprese nebo roztažení..
Práce, kterou pružina následně provede na bloku, je:
Žjaro = -Wext
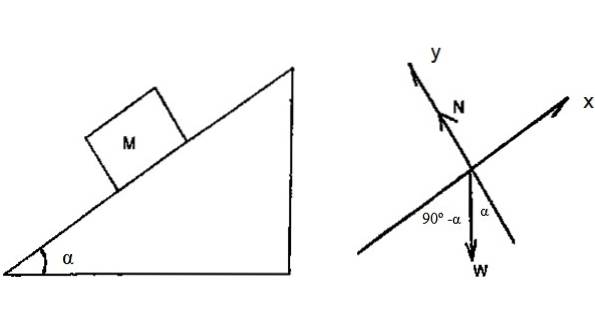
Blok na obrázku 4 má hmotnost M = 2 kg a bez tření sklouzává po nakloněné rovině, s α = 36,9 °. Za předpokladu, že je dovoleno sklouznout z klidu z vrcholu roviny, jejíž výška je h = 3 m, najděte pomocí věty o pracovní kinetické energii rychlost, s níž blok dosáhne základny roviny.
Diagram volného těla ukazuje, že jedinou silou, která je schopná pracovat na bloku, je hmotnost. Přesnější: složka hmotnosti podél osy x.
Vzdálenost uražená blokem v rovině se vypočítá pomocí trigonometrie:
d = 3 / (cos 36,9 °) m = 3,75 m
Žhmotnost = (Mg). d. cos (90-α) = 2 x 9,8 x 3,75 x cos 53,1 ° J = 44,1 J
Vědou o pracovní kinetické energii:
Žsíť = ΔK.
Žsíť = Whmotnost
ΔK = ½ MvFdva- ½ Mvnebodva
Protože je uvolněn z klidu, protinebo = 0, Tím pádem:
Žsíť = ½ MvFdva
Vodorovná pružina, jejíž konstanta je k = 750 N / m, je na jednom konci připevněna ke zdi. Osoba stlačuje druhý konec na vzdálenost 5 cm. Vypočítejte: a) sílu vyvíjenou danou osobou, b) práci, kterou udělal pro stlačení pružiny.
a) Velikost síly aplikované osobou je:
F = kx = 750 N / m. 5x10 -dva m = 37,5 N.
b) Pokud je konec pružiny původně na x1 = 0, odtud to vzít do konečné polohy xdva = 5 cm, je nutné provést následující práci podle výsledku získaného v předchozí části:
Žext = ½ k (xdvadva - X1dva) = 0,5 x 750 x (0,05dva -0dva) J = 0,9375 J.
Zatím žádné komentáře