
Vlastnosti rovnostranného trojúhelníku, vlastnosti, vzorce, plocha
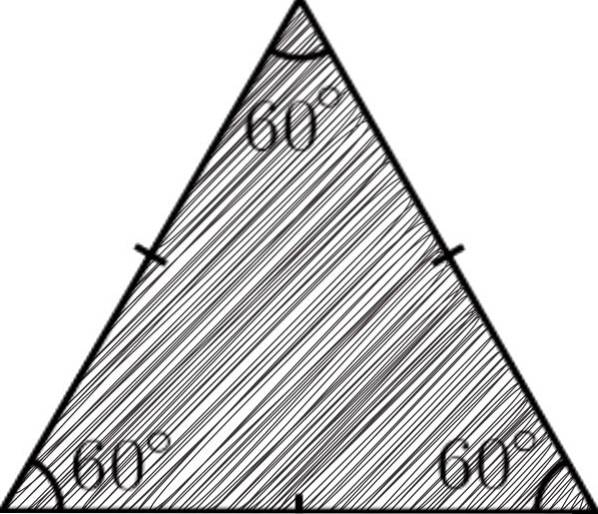
A rovnostranný trojúhelník je to mnohoúhelník se třemi stranami, kde jsou všechny stejné; to znamená, že mají stejnou míru. Pro tuto vlastnost byl dán název rovnostranný (rovné strany).
Trojúhelníky jsou polygony považované za nejjednodušší v geometrii, protože jsou tvořeny třemi stranami, třemi úhly a třemi vrcholy. V případě rovnostranného trojúhelníku, protože má stejné strany, znamená to, že jeho tři úhly budou také stejné..
Rejstřík článků
- 1 Charakteristika rovnostranných trojúhelníků
- 1.1 - Rovné strany
- 1.2 - Součásti
- 2 Vlastnosti
- 2.1 Vnitřní úhly
- 2.2 Vnější úhly
- 2.3 Součet stran
- 2.4 Shodné strany
- 2.5 Shodné úhly
- 3 Jak vypočítat obvod?
- 4 Jak vypočítat výšku?
- 5 Jak vypočítat strany?
- 6 Jak vypočítat plochu?
- 7 cvičení
- 7.1 - První cvičení
- 7.2 - Druhé cvičení
- 7.3 - Třetí cvičení
- 8 Reference
Charakteristika rovnostranných trojúhelníků
- Stejné strany
Rovnostranné trojúhelníky jsou ploché a uzavřené postavy, skládající se ze tří úseček. Trojúhelníky jsou klasifikovány podle jejich charakteristik, ve vztahu k jejich stranám a úhlům; rovnostranný byl klasifikován pomocí míry jeho stran jako parametru, protože jsou přesně stejné, to znamená, že jsou shodné.
Rovnostranný trojúhelník je zvláštním případem rovnoramenného trojúhelníku, protože dvě jeho strany jsou shodné. Proto jsou všechny rovnostranné trojúhelníky také rovnoramenné, ale ne všechny rovnoramenné trojúhelníky budou rovnostranné.
Tímto způsobem mají rovnostranné trojúhelníky stejné vlastnosti jako rovnoramenný trojúhelník..
Rovnostranné trojúhelníky lze také klasifikovat podle šířky jejich vnitřních úhlů jako rovnostranný ostrý trojúhelník, který má tři strany a tři vnitřní úhly se stejnou mírou. Úhly budou ostré, to znamená, že budou menší než 90nebo.
- Komponenty
Trojúhelníky obecně mají několik linií a bodů, které ji tvoří. Používají se k výpočtu plochy, stran, úhlů, mediánu, půlení, půlení a výšky..
- Medián: je přímka, která začíná od středu jedné strany a dosahuje opačného vrcholu. Tyto tři mediány se sbíhají v bodě zvaném barycentrum nebo těžiště..
- Bisector: je to paprsek, který rozděluje úhel vrcholů na dva úhly stejné míry, proto je známý jako osa symetrie. Rovnostranný trojúhelník má tři osy symetrie. V rovnostranném trojúhelníku je půlící čára nakreslena od vrcholu úhlu k jeho protilehlé straně a rozřízne ji ve svém středu. Setkávají se v bodě zvaném incenter.
- Prostřední: je segment kolmý na stranu trojúhelníku, která má svůj počátek uprostřed. Existují tři léky v trojúhelníku a setkávají se v bodě zvaném circumcenter.
- Výška: je přímka, která vede z vrcholu na stranu, která je naproti, a také tato přímka je kolmá na tuto stranu. Všechny trojúhelníky mají tři výšky, které se shodují v bodě zvaném orthocenter..
V následujícím grafu vidíme scalenový trojúhelník, kde jsou podrobně uvedeny některé ze zmíněných komponent
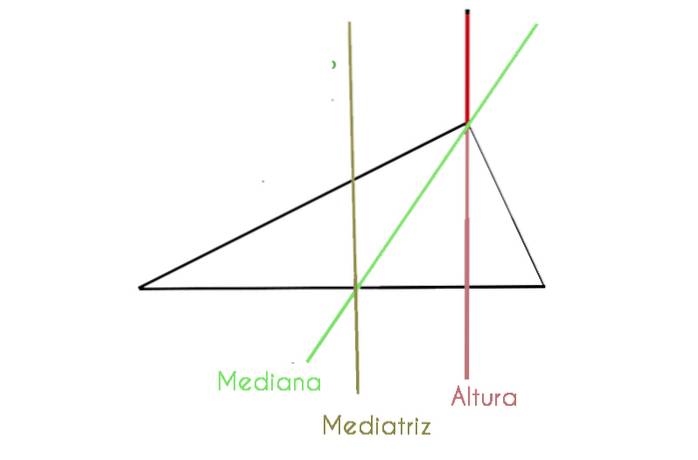
Bisektor, medián a bisektor jsou shodné
Bisektor rozděluje stranu trojúhelníku na dvě části. V rovnostranných trojúhelnících bude tato strana rozdělena na dvě přesně stejné části, tj. Trojúhelník bude rozdělen na dva shodné pravé trojúhelníky.
Tedy půlící čára nakreslená z jakéhokoli úhlu rovnostranného trojúhelníku se shoduje se střední a půlící stranou strany protilehlé tomuto úhlu..
Příklad:
Následující obrázek ukazuje trojúhelník ABC se středním bodem D, který rozděluje jednu z jeho stran na dva segmenty AD a BD.
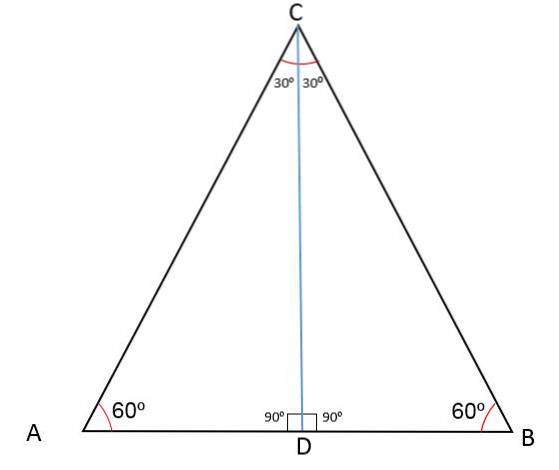
Nakreslením přímky z bodu D do protilehlého vrcholu se podle definice získá střední CD, které je relativní k vrcholu C a straně AB.
Vzhledem k tomu, že segment CD rozděluje trojúhelník ABC na dva stejné trojúhelníky CDB a CDA, znamená to, že bude mít shodný případ: strana, úhel, strana, a proto CD bude také půlící částí BCD.
Vynesením segmentu CD se dělí vrcholový úhel na dva stejné úhly 30nebo, úhel vrcholu A stále měří 60nebo a čára CD svírá úhel 90nebo vzhledem ke středu D.
Segmentové CD tvoří úhly, které mají stejnou míru pro trojúhelníky ADC a BDC, to znamená, že jsou doplňkové takovým způsobem, že míra každého z nich bude:
Med. (ADB) + Med. (ADC) = 180nebo
dva * Med. (ADC) = 180nebo
Med. (ADC) = 180nebo ÷ 2
Med. (ADC) = 90nebo.
Takže máme segment CD, který je také půlící stranou strany AB.
Oseška a výška jsou shodné
Nakreslením půlící čáry z vrcholu jednoho úhlu do středu opačné strany rozdělí rovnostranný trojúhelník na dva shodné trojúhelníky.
Takovým způsobem, že je vytvořen úhel 90 °nebo (že jo). To naznačuje, že tento úsečkový segment je zcela kolmý na tuto stranu a podle definice by touto úsečkou byla výška.
Tímto způsobem se půlící úhel libovolného úhlu rovnostranného trojúhelníku shoduje s výškou vzhledem k opačné straně tohoto úhlu..
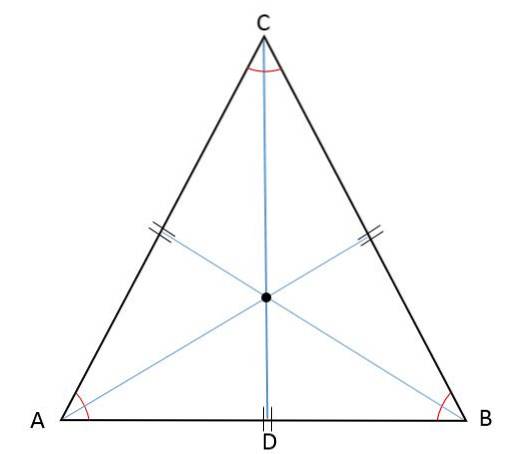
Ortocentrum, barycentrum, incenter a shodný circumcenter
Vzhledem k tomu, že výška, medián, přímka a přímka jsou reprezentovány stejným segmentem současně, v rovnostranném trojúhelníku budou body setkání těchto segmentů - orthocenter, bisector, incenter a circumcenter - nalezeny ve stejném bodě:
Vlastnosti
Hlavní vlastností rovnostranných trojúhelníků je, že vždy budou rovnoramennými trojúhelníky, protože rovnorameny jsou tvořeny dvěma shodnými stranami a rovnostrannými třemi..
Tímto způsobem rovnostranné trojúhelníky zdědily všechny vlastnosti rovnoramenného trojúhelníku:
Vnitřní úhly
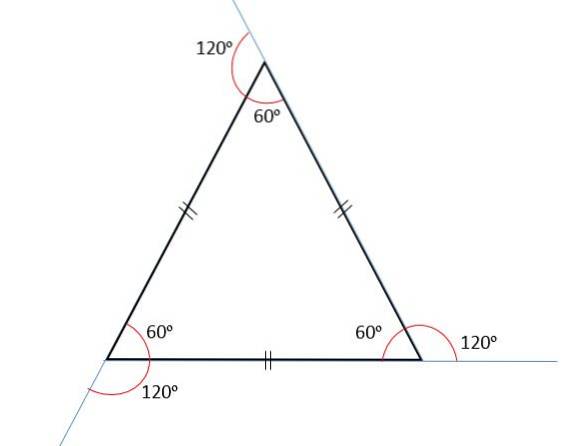
Součet vnitřních úhlů se vždy rovná 180nebo, a protože všechny jeho úhly jsou shodné, pak každý z nich bude měřit 60nebo.
Vnější úhly
Součet vnějších úhlů se bude vždy rovnat 360nebo, proto každý vnější úhel bude měřit 120nebo. Je to proto, že vnitřní a vnější úhly jsou doplňkové, to znamená, že když je přidáme, budou se vždy rovnat 180nebo.
Součet stran
Součet měr dvou stran musí být vždy větší než míra třetí strany, tj. A + b> c, kde a, b a c jsou měrami každé strany.
Shodné strany
Rovnostranné trojúhelníky mají všechny tři strany se stejnou mírou nebo délkou; to znamená, že jsou shodní. Proto v předchozí položce máme, že a = b = c.
Shodné úhly
Rovnostranné trojúhelníky jsou také známé jako rovnoramenné trojúhelníky, protože jejich tři vnitřní úhly jsou navzájem shodné. Je to proto, že všechny jeho strany mají také stejné měření.
Jak vypočítat obvod?
Obvod mnohoúhelníku se vypočítá sečtením stran. Protože v tomto případě má rovnostranný trojúhelník všechny jeho strany se stejnou mírou, jeho obvod se počítá podle následujícího vzorce:
P = 3 * boční.
Jak vypočítat výšku?
Vzhledem k tomu, že výška je přímka kolmá k základně, rozděluje ji na dvě stejné části prodloužením do opačného vrcholu. Tak vznikají dva rovné trojúhelníky.
Výška (h) představuje protilehlou nohu (a), polovinu boční AC k sousední noze (b) a boční BC představuje přeponu (c).
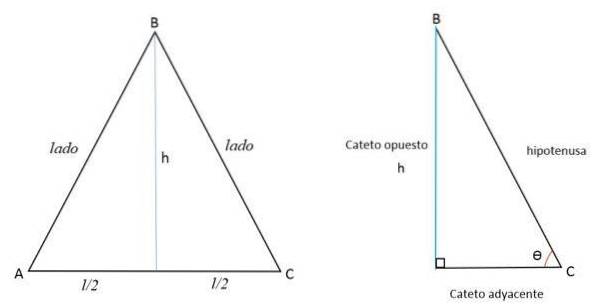
Pomocí Pythagorovy věty lze určit hodnotu výšky:
nadva + bdva = cdva
Kde:
nadva = výška (h).
bdva = strana b / 2.
Cdva = strana a.
Dosazením těchto hodnot do Pythagorovy věty a řešením výšky máme:
hdva + ( l / dva)dva = ldva
hdva + ldva/ 4 = ldva
hdva = ldva - ldva/ 4
hdva = (4*ldva - ldva) / 4
hdva = 3*ldva /4
√hdva = √ (3*ldva /4)

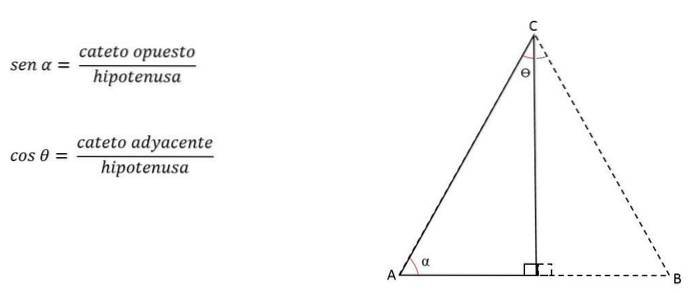
Pokud je známý úhel tvořený shodnými stranami, lze výšku (představovanou nohou) vypočítat použitím trigonometrických poměrů.
Nohy se nazývají protilehlé nebo sousedící v závislosti na úhlu, který se bere jako reference..
Například na obrázku nad bude noha h opačná pro úhel C, ale sousedící s úhlem B:
Výšku tedy lze vypočítat pomocí:
Jak vypočítat strany?
Existují případy, kdy míry stran trojúhelníku nejsou známy, ale jejich výška a úhly vytvořené na vrcholech.
Pro určení oblasti je v těchto případech nutné použít trigonometrické poměry.
Znát úhel jednoho z jeho vrcholů, nohy jsou identifikovány a je použit odpovídající trigonometrický poměr:
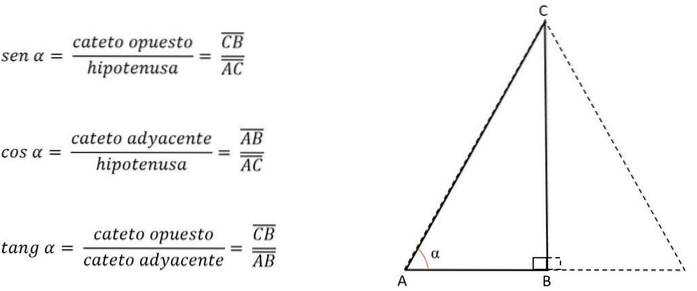
Noha AB bude tedy opačná pro úhel C, ale sousedí s úhlem A. V závislosti na straně nebo noze odpovídající výšce je druhá strana uvolněna, aby získala svou hodnotu, s vědomím, že v rovnostranném trojúhelníku budou tři strany vždy mít stejné měření.
Jak vypočítat plochu?
Plocha trojúhelníků se vždy počítá se stejným vzorcem, vynásobením základu krát výška a dělením dvěma:
Plocha = (nar * h) ÷ 2
S vědomím, že výška je dána vzorcem:

Výcvik
- První cvičení
Boky rovnostranného trojúhelníku ABC jsou každá po 20 cm. Vypočítejte výšku a plochu polygonu.
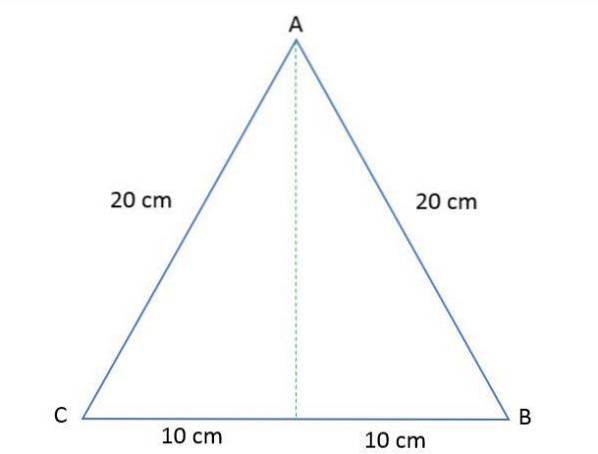
Řešení
Chcete-li určit plochu tohoto rovnostranného trojúhelníku, je nutné vypočítat výšku s vědomím, že při kreslení rozdělí trojúhelník na dva stejné pravé trojúhelníky.
Tímto způsobem lze Pythagorovu větu použít k jejímu nalezení:
nadva + bdva = cdva
Kde:
a = 20/2 = 10 cm.
b = výška.
c = 20 cm.
Data jsou ve větě nahrazena:
10dva + bdva = 20dva
100 cm + bdva = 400 cm
bdva = (400 - 100) cm
bdva = 300 cm
b = √ 300 cm
b = 17,32 cm.
To znamená, že výška trojúhelníku se rovná 17,32 cm. Nyní je možné vypočítat plochu daného trojúhelníku dosazením do vzorce:
Plocha = (nar * h) ÷ 2
Plocha = (20 cm * 17,32 cm) ÷ 2
Plocha = 346,40 cmdva ÷ 2
Plocha = 173,20 cmdva.
Dalším jednodušším způsobem řešení cvičení je nahrazení dat v přímém vzorci pro oblast, kde se implicitně také nachází hodnota výšky:

- Druhé cvičení
Květy budou zasazeny na kousek země, který má tvar rovnostranného trojúhelníku. Pokud je obvod této země roven 450 m, vypočítejte počet metrů čtverečních, které květiny obsadí.
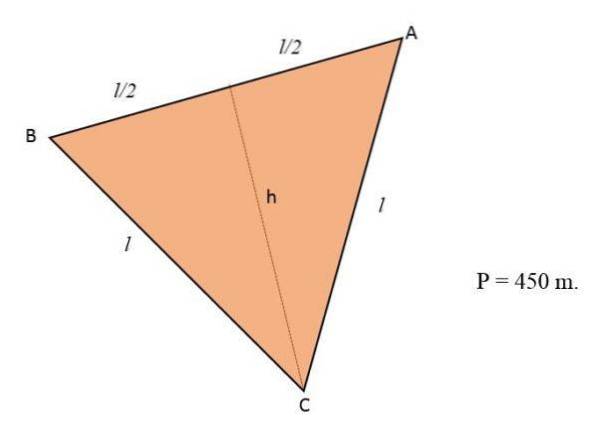
Řešení
S vědomím, že obvod trojúhelníku odpovídá součtu jeho tří stran, a protože terén má tvar rovnostranného trojúhelníku, budou mít jeho tři strany stejnou míru nebo délku:
P = strana + strana + strana = 3 * l
3 * l = 450 m.
l = 450 m ÷ 3
l = 150 m.
Nyní je pouze nutné vypočítat výšku tohoto trojúhelníku.
Výška rozděluje trojúhelník na dva shodné pravé trojúhelníky, kde jedna noha představuje výšku a druhá polovina základny. Podle Pythagorovy věty lze určit výšku:
nadva + bdva = cdva
Kde:
na = 150 m ÷ 2 = 75 m.
C = 150 m.
b = výška
Data jsou ve větě nahrazena:
(75 m)dva + bdva = (150 m)dva
5 625 m + bdva = 22 500 m
bdva = 22 500 m - 5625 m
bdva = 16 875 m
b = √ 16 875 m
b = 129,90 m.
Oblast, kterou květiny obsadí, bude tedy:
Plocha = b * h ÷ 2
Plocha = (150 m * 129,9 m) ÷ 2
Plocha = (19 485 mdva) ÷ 2
Plocha = 9 742,5 mdva
- Třetí cvičení
Rovnostranný trojúhelník ABC je rozdělen úsečkou, která vede z jeho vrcholu C do středu D, který se nachází na opačné straně (AB). Tento segment měří 62 metrů. Vypočítejte plochu a obvod tohoto rovnostranného trojúhelníku.
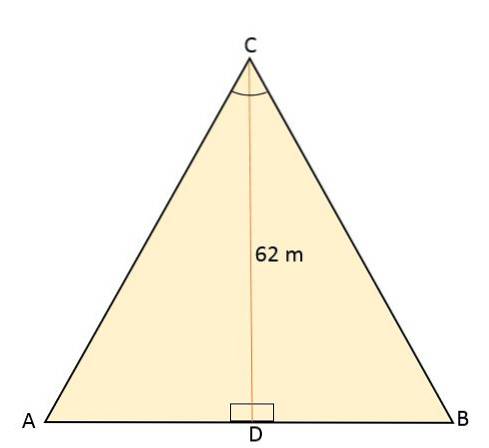
Řešení
S vědomím, že rovnostranný trojúhelník je rozdělen úsečkou, která odpovídá výšce, čímž vznikají dva shodné pravé trojúhelníky, to také dělí úhel vrcholu C na dva úhly se stejnou mírou, 30nebo každý.
Výška tvoří úhel 90nebo vzhledem k segmentu AB a úhel vrcholu A pak bude měřit 60nebo.
Poté použijte úhel 30 jako referencinebo, výška CD je nastavena jako noha přiléhající k úhlu a BC jako přepona.
Z těchto údajů lze určit hodnotu jedné ze stran trojúhelníku pomocí trigonometrických poměrů:
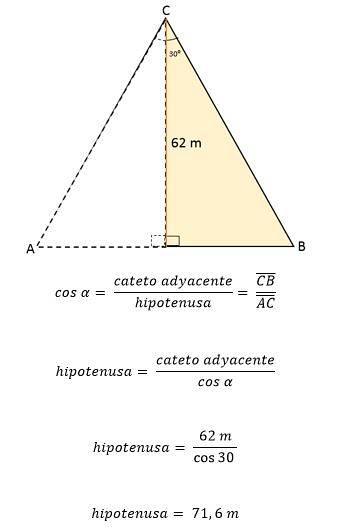
Protože v rovnostranném trojúhelníku mají všechny strany přesně stejnou míru nebo délku, znamená to, že každá strana rovnostranného trojúhelníku ABC je rovna 71,6 metru. S vědomím toho je možné určit jeho oblast:
Plocha = b * h ÷ 2
Plocha = (71,6 m * 62 m) ÷ 2
Plocha = 4 438,6 mdva ÷ 2
Plocha = 2219,3 mdva
Obvod je dán součtem jeho tří stran:
P = strana + strana + strana = 3 * l
P = 3*l
P = 3 * 71,6 m
P = 214,8 m.
Reference
- Álvaro Rendón, A. R. (2004). Technický výkres: kniha aktivit.
- Arthur Goodman, L. H. (1996). Algebra a trigonometrie s analytickou geometrií. Pearson Education.
- Baldor, A. (1941). Algebra. Havana: Kultura.
- BARBOSA, J. L. (2006). Rovinná euklidovská geometrie. SBM. Rio de Janeiro, .
- Coxford, A. (1971). Geometrie Transformační přístup. USA: Laidlaw Brothers.
- Euclid, R. P. (1886). Euklidovy prvky geometrie.
- Héctor Trejo, J. S. (2006). Geometrie a trigonometrie.
- León Fernández, G. S. (2007). Integrovaná geometrie. Metropolitní technologický institut.
- Sullivan, J. (2006). Algebra a trigonometrie. Pearson Education.


Zatím žádné komentáře