
Definice vektorových týmových čoček, notace, cvičení
Dva nebo více vektory jsou týmové čočky pokud mají stejný modul, stejný směr a stejný smysl, i když je jejich výchozí bod odlišný. Pamatujte, že vlastnosti vektoru jsou přesné: počátek, modul, směr a smysl.
Vektory jsou reprezentovány orientovaným segmentem nebo šipkou. Obrázek 1 ukazuje znázornění několika vektorů v rovině, z nichž některé jsou týmové čočky podle původně dané definice..
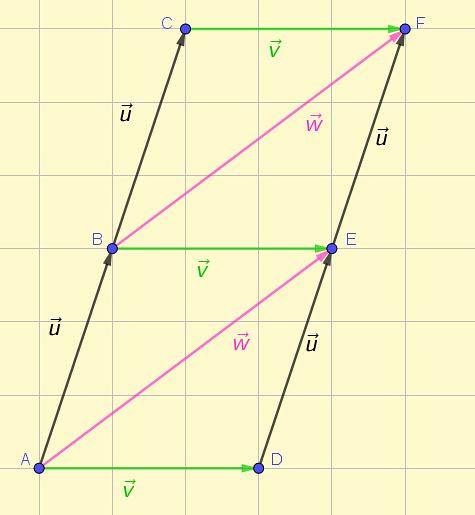
Na první pohled je možné vidět, že tři zelené vektory mají stejnou velikost, stejný směr a stejný smysl. Totéž lze říci o dvou růžových vektorech a čtyřech černých vektorech.
Mnoho přírodních veličin má chování podobné vektorům, například rychlost, zrychlení a síla. Proto je důležité je správně charakterizovat.
Rejstřík článků
- 1 Zápis pro vektory a zařízení
- 1.1 Volné, posuvné a protilehlé vektory
- 2 Cvičení
- 2.1 - Cvičení 1
- 2.2 - Cvičení 2
- 2.3 - Cvičení 3
- 3 Odkazy
Zápis pro vektory a zařízení
K rozlišení vektorových veličin od skalárních veličin se často používá tučné písmo nebo šipka nad písmenem. Při ruční práci s vektory na notebooku je nutné je odlišit šipkou a při použití tištěného média se použije tučný typ.
Vektory lze označit uvedením jejich výchozího bodu nebo místa původu a jejich výchozího bodu. Například AB, před naším letopočtem, Z Y EF z obrázku 1 jsou místo toho vektory AB, před naším letopočtem, Z Y EF jsou skalární veličiny nebo čísla, která označují velikost, modul nebo velikost jejich příslušných vektorů.
Pro označení, že dva vektory jsou týmově orientované, symbol „∼ ". S touto notací můžeme na obrázku poukázat na následující vektory, které jsou navzájem týmově orientované:
AB∼BC∼DE∼EF
Všichni mají stejnou velikost, směr a význam. Proto splňují výše uvedená nařízení..
Volné, posuvné a opačné vektory
Libovolný z vektorů na obrázku (například AB) je zástupcem sady všech vektorů fixovaných objektivem. Tato nekonečná sada definuje třídu volných vektorů nebo.
nebo = AB, BC, DE, EF, ...
Alternativní notace je následující:
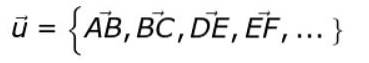
Pokud tučná nebo malá šipka nejsou umístěny nad písmenem nebo, je, že chceme odkázat na vektorový modul nebo.
Volné vektory se neaplikují na žádný konkrétní bod.
Pro jejich část posuvné vektory Jsou to vektory délky týmu k danému vektoru, ale jejich aplikační bod musí být obsažen v akční linii daného vektoru.
A opačné vektory Jsou to vektory, které mají stejnou velikost a směr, ale opačné smysly, ačkoli v anglických textech se jim říká de opačným směrem protože směr také naznačuje smysl. Opačné vektory nejsou týmy.
Výcvik
-Cvičení 1
Které další vektory z vektorů zobrazených na obrázku 1 jsou navzájem týmové??
Řešení
Kromě těch, které již byly uvedeny v předchozí části, je z obrázku 1 patrné, že INZERÁT, BÝT Y ES Jsou to také vektory délky týmu:
REKLAMA ∼ BE ∼ CE
Kterýkoli z nich představuje třídu volných vektorů proti.
Vektory AE Y BF :
AE ∼ BF
Kdo jsou zástupci třídy w.
-Cvičení 2
Body A, B a C jsou na kartézské rovině XY a jejich souřadnice jsou:
A = (- 4,1), B = (- 1,4) a C = (- 4, -3)
Najděte souřadnice čtvrtého bodu D tak, aby vektory AB Y CD být orientovaný na tým.
Řešení
Aby CD být orientovaný na tým AB musí mít stejný modul a stejnou adresu jako AB .
Modul AB na druhou je:
|AB| ^ 2 = (-1 - (-4)) ^ 2 + (4 -1) ^ 2 = 9 + 9 = 18
Souřadnice D nejsou známy, takže můžeme říci: D = (x, y)
Pak: |CD| ^ 2 = (x - (- 4)) ^ 2 + (y - (-3)) ^ 2
Jako |AB| = |CD| je jednou z podmínek pro AB Y CD orientovaný na tým, máte:
(x + 4) ^ 2 + (y + 3) ^ 2 = 18
Protože máme dvě neznámé, je zapotřebí další rovnice, kterou lze získat z podmínky, že AB Y CD jsou paralelní a ve stejném smyslu.
Sklon vektoru AB
Vektorový sklon AB označuje vaši adresu:
Sklon AB = (4 -1) / (- 1 - (-4)) = 3/3 = 1
Označující, že vektor AB 45 ° s osou X..
Vector CD sklon
Sklon CD se vypočítá podobným způsobem:
Sklon CD = (y - (-3)) / (x - (- 4)) = (y + 3) / (x + 4)
Rovnání tohoto výsledku se sklonem AB máme následující rovnici:
y + 3 = x + 4
Což znamená, že y = x + 1.
Pokud je tento výsledek nahrazen v rovnici pro rovnost modulů, máme:
(x + 4) ^ 2 + (x + 1 + 3) ^ 2 = 18
Zjednodušení zůstává:
2 (x + 4) ^ 2 = 18,
Což odpovídá:
(x + 4) ^ 2 = 9
To znamená, že x + 4 = 3, což znamená, že x = -1. Souřadnice D jsou tedy (-1, 0).
šek
Složky vektoru AB are (-1 - (- 4), 4 -1) = (3, 3)
a vektor CD jsou (-1 - (- 4)); 0 - (- 3)) = (3, 3)
Což znamená, že vektory jsou týmově orientované. Pokud dva vektory mají stejné kartézské komponenty, mají stejný modul a směr, proto jsou týmové čočky..
-Cvičení 3
Volný vektor nebo má velikost 5 a směr 143,1301 °.
Najděte jejich kartézské komponenty a určete souřadnice bodů B a C s vědomím, že fixní vektory AB a CD jsou týmově orientované na u. Souřadnice A jsou (0, 0) a souřadnice bodu C jsou (-3,2).
Řešení
Situaci, kterou cvičení představuje, lze znázornit následujícím obrázkem:
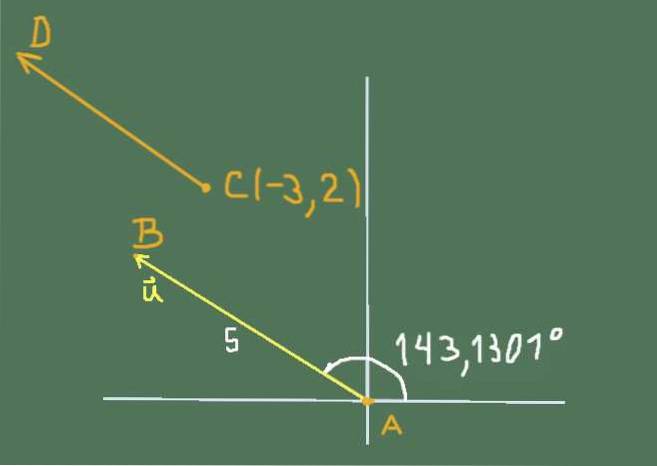
Kartézské složky nebo Oni jsou
nebo = (5 * cos (143,1301 °); 5 * hřích (143,1301 °))
Při výpočtu zůstává:
nebo = (-4,3)
Souřadnice B nejsou známy, takže umístíme B (x, y)
Souřadnice vektoru AB are (x-0; y-0), ale protože u je týmová čočka, musí být splněna rovnost složek, proto vyplývá, že souřadnice B jsou (-4, 3).
Podobně souřadnice vektoru CD jsou (x - (- 3)); (a - 2), že musí být týmově orientovaný u, lnebo vedoucí k:
x + 3 = -4 a y -2 = 3
Pak budou souřadnice bodu D (-7, 5).
Reference
- Calculus.cc. Opravený vektor. Volný vektor. Obnoveno z: Calclo.cc
- Descartes 2d. Pevné vektory a vektory volného letadla. Obnoveno z: recursostic.educacion.es
- Projekt Guao. Vektory týmové čočky. Obnoveno z: guao.org
- Resnick, R., Krane, K. (2001). Fyzika. New York: John Wiley & Sons.
- Serway, R.; Jewett, John W. (2004). Fyzika pro vědce a inženýry (6. vydání). Brooks / Cole.
- Tipler, Paul A. (2000). Fyzika pro vědu a techniku. Svazek I. Barcelona: Ed. Reverté.
- Weisstein, E. "Vektor." Ve Weissteinu Eric W. MathWorld. Wolfram Research.



Zatím žádné komentáře