
Vlastnosti volných vektorů, příklady, cvičení
The volné vektory Jsou to ty, které jsou plně specifikovány svou velikostí, směrem a smyslem, aniž by bylo nutné označovat bod aplikace nebo konkrétní původ.
Protože nekonečné vektory lze kreslit tímto způsobem, volný vektor není jediná entita, ale sada paralelních a identických vektorů, které jsou nezávislé na tom, kde jsou..
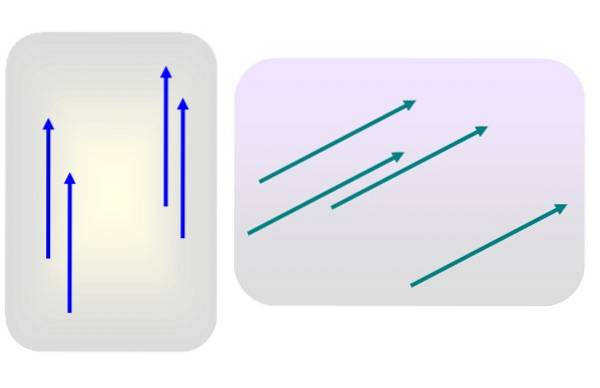
Řekněme, že máme několik vektorů velikosti 3 nasměrovaných svisle nahoru nebo velikosti 5 a nakloněných doprava, jako na obrázku 1.
Ani jeden z těchto vektorů není konkrétně použit v jakémkoli bodě. Pak je kterýkoli z modrých nebo zelených vektorů reprezentativní pro jejich příslušnou skupinu, protože jejich charakteristiky - modul, směr a smysl - se při přenosu na jiné místo v rovině vůbec nezmění..
Volný vektor je obvykle v tištěném textu označen například tučným malým písmem proti. Nebo s malými písmeny a šipkou nahoře, pokud jde o ručně psaný text.
Rejstřík článků
- 1 Příklady
- 1.1 Vlastnosti a vlastnosti
- 2 Vyřešená cvičení
- 2.1 - Cvičení 1
- 2.2 Cvičení 2
- 3 Odkazy
Příklady
Výhodou volných vektorů je, že je lze pohybovat rovinou nebo prostorem a udržovat jejich vlastnosti, protože jakýkoli zástupce množiny je stejně platný.
Proto se ve fyzice a mechanice často používají. Například pro označení lineární rychlosti pohybujícího se tělesa není nutné zvolit konkrétní bod na objektu. Vektor rychlosti se tedy chová jako volný vektor.
Dalším příkladem volného vektoru je dvojice sil. A pár Skládá se ze dvou sil stejné velikosti a směru, ale opačných směrů, působících v různých bodech na těleso. Účinkem páru není přeložit objekt, ale způsobit rotaci díky okamžik vyrobeno.
Obrázek 2 ukazuje několik sil působících na volant. Prostřednictvím sil F1 Y Fdva, vytváří se točivý moment, který otáčí setrvačníkem kolem jeho středu a ve směru hodinových ručiček.
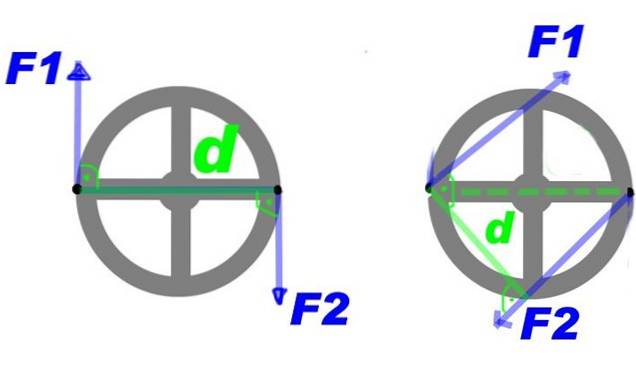
Můžete provést určité změny točivého momentu a stále získat stejný rotační efekt, například zvýšit sílu, ale zmenšit vzdálenost mezi nimi. Nebo udržujte sílu a vzdálenost, ale aplikujte točivý moment na jiný pár bodů na volantu, to znamená, otáčejte točivým momentem kolem středu.
Okamžik dvojice sil nebo jednoduše pár, je vektor, jehož modul je Fd a je směrován kolmo k rovině setrvačníku. V příkladu ukázaném konvencí má rotace ve směru hodinových ručiček negativní smysl.
Vlastnosti a vlastnosti
Na rozdíl od volného vektoru v jsou vektory AB Y CD jsou pevné (viz obrázek 3), protože mají zadaný výchozí bod a bod příjezdu. Ale protože jsou navzájem shovívaví k týmu a zase k vektoru proti, jsou reprezentativní pro volný vektor proti.

Hlavní vlastnosti volných vektorů jsou následující:
-Libovolný vektor AB (viz obrázek 2) je, jak bylo řečeno, reprezentativní pro volný vektor proti.
-Modul, směr a smysl jsou u každého zástupce volného vektoru stejné. Na obrázku 2 jsou vektory AB Y CD představují volný vektor proti a jsou orientovaní na tým.
-Vzhledem k bodu P v prostoru je vždy možné najít zástupce volného vektoru proti jehož původ je v P a uvedený zástupce je jedinečný. Toto je nejdůležitější vlastnost volných vektorů a ta, díky níž jsou tak univerzální.
-Nulový volný vektor je označen jako 0 y je množina všech vektorů, kterým chybí velikost, směr a smysl.
-Pokud vektor AB představuje volný vektor proti, pak vektor BA představuje volný vektor -proti.
-Bude použita notace PROTI3 označit množinu všech volných vektorů prostoru a PROTIdva označit všechny volné vektory roviny.
Vyřešená cvičení
S volnými vektory lze provádět následující operace:
-Součet
-Odčítání
-Násobení skaláru vektorem
-Skalární součin mezi dvěma vektory.
-Křížový součin mezi dvěma vektory
-Lineární kombinace vektorů
A více.
-Cvičení 1
Student se pokouší plavat z jednoho bodu na břehu řeky do druhého, který je přímo naproti. Aby toho bylo dosaženo, nic přímo při rychlosti 6 km / h, v kolmém směru, ale proud má rychlost 4 km / h, která ji vychýlí.
Vypočítejte výslednou rychlost plavce a kolik je proudem vychýlen.
Řešení
Výsledná rychlost plavce je vektorovým součtem jeho rychlosti (vzhledem k řece, nakreslené svisle nahoru) a rychlosti řeky (nakreslené zleva doprava), která se provádí podle obrázku níže:
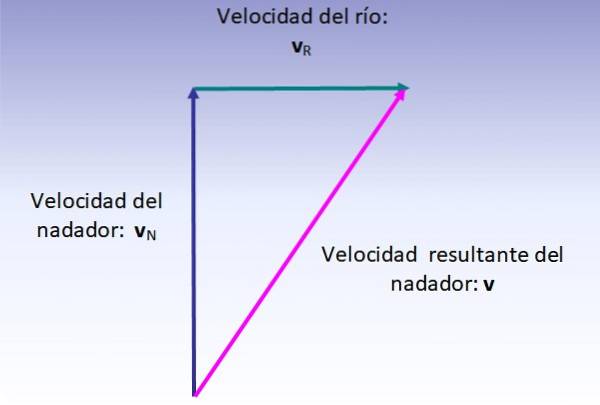
Velikost výsledné rychlosti odpovídá přeponě zobrazeného pravoúhlého trojúhelníku, proto:
v = (6dva + 4dva) ½ km / h = 7,2 km / h
Směr lze vypočítat pomocí úhlu vzhledem ke kolmici na břeh:
α = arctg (4/6) = 33,7 ° nebo 56,3 ° vzhledem ke břehu.
Cvičení 2
Najděte okamžik páru zobrazený na obrázku:
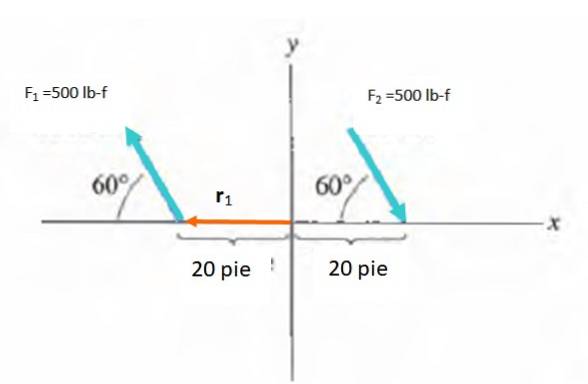
Řešení
Moment se vypočítá podle:
M = r X F
Jednotky okamžiku jsou lb-f.ft. Jelikož je točivý moment v rovině obrazovky, je moment směrován kolmo na ni, a to buď směrem ven nebo dovnitř..
Protože krouticí moment v příkladu má tendenci otáčet objektem, na který je aplikován (což na obrázku není zobrazeno) ve směru hodinových ručiček, považuje se tento moment za směřující k vnitřní straně obrazovky se záporným znaménkem.
Velikost momentu je M = F.d. v a, kde a je úhel mezi silou a vektorem r. Musíte zvolit bod, ve vztahu ke kterému se má vypočítat moment, což je volný vektor. Proto je zvolen původ referenčního systému r jde z O do bodu aplikace každé síly.
M1 = M.dva = -Fdsen60º = -500. 20 .sin 60º lb-f. ft = -8660,3 lb-f. chodidlo
Čistý moment je součtem M1 a M.dva: -17329,5 lb-f. chodidlo.
Reference
- Beardon, T. 2011. Úvod do vektorů. Citováno z: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Fyzika pro vědy a inženýrství. Svazek 1. Kinematika. 31-68.
- Fyzický. Modul 8: Vektory. Obnoveno z: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanics for Engineers. Statický. 6. vydání. Continental Publishing Company. 15-53.
- Kalkulačka sčítání vektorů. Obnoveno z: 1728.org
- Vektory. Obnoveno z: en.wikibooks.org
Zatím žádné komentáře