
Definice nekoplanárních vektorů, podmínky, cvičení
The neplanární vektory jsou ti, kteří nesdílejí stejné letadlo. Dva volné vektory a bod definují jednu rovinu. Třetí vektor může nebo nemusí sdílet tuto rovinu, a pokud ne, jsou to nekoplanární vektory.
Nekoplanární vektory nemohou být reprezentovány ve dvourozměrných prostorech jako tabule nebo list papíru, protože některé z nich jsou obsaženy ve třetí dimenzi. Abyste je mohli správně reprezentovat, musíte použít perspektivu.
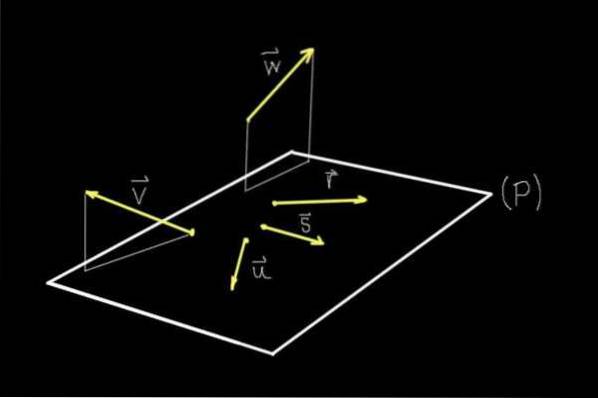
Podíváme-li se na obrázek 1, všechny zobrazené objekty jsou přísně v rovině obrazovky, ale díky perspektivě si náš mozek dokáže představit rovinu (P), která z ní vychází..
Na této rovině (P) jsou vektory r, s, nebo, zatímco vektory proti Y w nejsou v tom letadle.
Proto vektory r, s, nebo jsou koplanární nebo koplanární navzájem, protože sdílejí stejnou rovinu (P). Vektory proti Y w nesdílejí rovinu s žádným z ostatních zobrazených vektorů, proto nejsou koplanární.
Rejstřík článků
- 1 Koplanární vektory a rovnice roviny
- 1.1 Kartézská rovnice roviny
- 2 Podmínky pro to, aby tři vektory nebyly koplanární
- 2.1 Podmínka nekoplanárnosti
- 2.2 Alternativní podmínka nekoplanárnosti
- 3 Vyřešená cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Koplanární vektory a rovnice roviny
Rovina je jednoznačně definována, pokud se v trojrozměrném prostoru vyskytnou tři body.
Předpokládejme, že tyto tři body jsou bodem NA, směřovat B a pointa C které definují rovinu (P). S těmito body je možné sestrojit dva vektory AB = u Y AC = v které jsou konstrukčně koplanární s rovinou (P).
Vektorový produkt (nebo křížový produkt) těchto dvou vektorů má za následek, že třetí vektor je na ně kolmý (nebo normální) a je tedy kolmý k rovině (P):
n = u X proti => n ⊥ nebo Y n ⊥ proti => n ⊥ (P)
Jakýkoli jiný bod, který patří k rovině (P) musí uspokojit, že vektor AQ je kolmá na vektor n; To odpovídá tvrzení, že tečkovaný produkt (nebo tečkovaný produkt) z n s AQ musí být nula:
n • AQ = 0 (*)
Předchozí podmínka odpovídá tomu, že:
AQ • (nebo X proti) = 0
Tato rovnice zajišťuje, že bod Q patří do letadla (P).
Kartézská rovnice roviny
Výše uvedenou rovnici lze napsat v kartézské formě. K tomu napíšeme souřadnice bodů NA, Q a složky normálního vektoru n:
A = (a, b, c)
Q = (x, y, z)
n= (nx, ny, nz)
Takže komponenty AQ jsou:
AQ= (x-a, y-b, z-c)
Podmínka pro vektor AQ je obsažen v rovině (P) je podmínka (*), která se nyní píše takto:
(nx, ny, nz) • (x-a, y-b, z-c) = 0
Výpočet tečkovaného produktu zůstává:
nx (x-a) + ny (y-b) + nz (z-b) = 0
Pokud je vyvinut a přeskupen, zůstává:
nx x + ny y + nz z = nx a + ny b + nz c
Předchozí výraz je kartézská rovnice roviny (P), jako funkce složek vektoru normálních k (P) a souřadnice bodu NA kterému patří (P).
Podmínky pro to, aby tři vektory nebyly koplanární
Jak je vidět v předchozí části, stav AQ • (nebo X proti) = 0 zaručuje, že vektor AQ je koplanární s nebo Y proti.
Pokud zavoláme w na vektor AQ pak můžeme potvrdit, že:
w, nebo Y proti jsou koplanární, právě když w • ( nebo X proti ) = 0.
Podmínka nekoplanárnosti
Pokud se trojitý produkt (nebo smíšený produkt) tří vektorů liší od nuly, pak tyto tři vektory nejsou koplanární.
Ano w • ( nebo X proti ) ≠ 0 pak vektory u, v a w nejsou koplanární.
Pokud jsou zavedeny kartézské složky vektorů u, v a w, lze podmínku nekoplanárnosti zapsat takto:
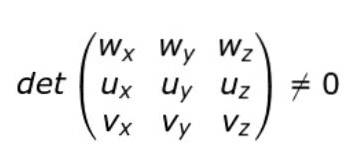
Trojitý produkt má geometrickou interpretaci a představuje objem rovnoběžnostěnu generovaný třemi nekoplanárními vektory.
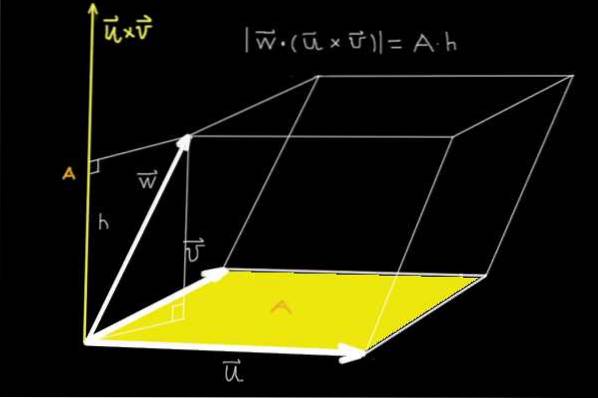
Důvod je následující; Když jsou dva z nekoplanárních vektorů vektorově násobeny, získá se vektor, jehož velikost je oblast rovnoběžníku, který generují.
Když je pak tento vektor skalárně vynásoben třetím nekoplanárním vektorem, máme projekci na vektor kolmý na rovinu určenou prvními dvěma vynásobenými oblastí, kterou určují..
To znamená, že máme plochu rovnoběžníku generovanou prvními dvěma vynásobenou výškou třetího vektoru.
Alternativní podmínka nekoplanárnosti
Pokud máte tři vektory a některý z nich nelze zapsat jako lineární kombinaci ostatních dvou, pak tyto tři vektory nejsou koplanární. To jsou tři vektory nebo, proti Y w nejsou koplanární, pokud je splněna podmínka:
α nebo + β proti + y w = 0
Je splněno, pouze když α = 0, β = 0 a γ = 0.
Vyřešená cvičení
-Cvičení 1
Existují tři vektory
nebo = (-3, -6, 2); proti = (4, 1, 0) a w = (-1, 2, z)
Všimněte si, že složka z vektoru w Není známo.
Najděte rozsah hodnot, které z může nabývat takovým způsobem, aby bylo zaručeno, že tři vektory nesdílejí stejnou rovinu.
Řešení
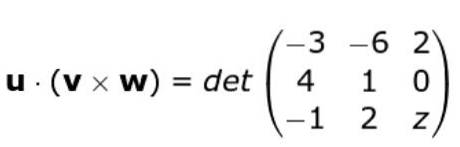
w • ( nebo X proti ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18
Nastavili jsme tento výraz rovný hodnotě nula
21 z + 18 = 0
a řešíme pro z
z = -18 / 21 = -6/7
Pokud by proměnná z měla hodnotu -6/7, byly by tři vektory koplanární.
Takže hodnoty z, které zaručují, že vektory nejsou koplanární, jsou hodnoty v následujícím intervalu:
z ∈ (-∞, -6 / 7) U (-6/7, ∞)
-Cvičení 2
Najděte objem rovnoběžnostěnu zobrazený na následujícím obrázku:
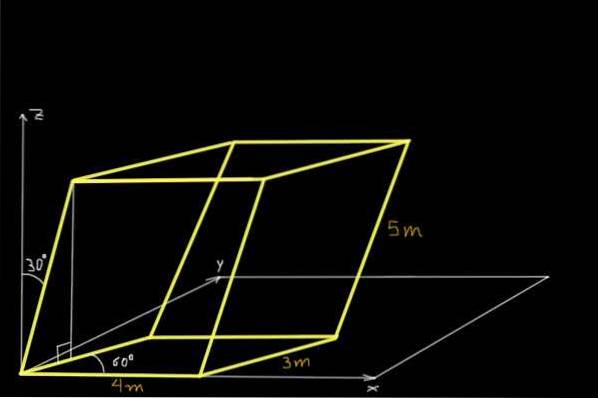
Řešení
Pro nalezení objemu rovnoběžnostěnu zobrazeného na obrázku budou určeny kartézské složky tří souběžných nekoplanárních vektorů na počátku souřadnicového systému. První je vektor nebo 4 m a rovnoběžně s osou X:
nebo= (4, 0, 0) m
Druhým je vektor proti v rovině XY o velikosti 3 m tvořící 60 ° s osou X:
proti= (3 * cos 60 °, 3 * sin 60 °, 0) = (1,5; 2,6; 0,0) m
A třetí vektor w 5 m a jehož výstupek v rovině XY tvoří 60 ° s osou X, navíc w tvoří 30 ° s osou Z.
w= (5 * hřích 30 ° * cos 60 °, 5 * hřích 30 ° * hřích 60 °, 5 * hřích 30 °)
Jakmile byly výpočty provedeny, máme: w= (1,25; 2,17; 2,5) m.
Reference
- Figueroa, D. Series: Fyzika pro vědy a inženýrství. Svazek 1. Kinematika. 31-68.
- Fyzický. Modul 8: Vektory. Obnoveno z: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanics for Engineers. Statický. 6. vydání. Continental Publishing Company 28-66.
- Série McLean, W. Schaum. Mechanika pro inženýry: statika a dynamika. 3. vydání. McGraw Hill. 1-15.
- Wikipedia. Vektor. Obnoveno z: es.wikipedia.org


Zatím žádné komentáře